【LeetCode】45.跳跃游戏2
题目链接
https://leetcode-cn.com/problems/jump-game-ii/
题目描述
给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例: 输入: [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。 说明: 假设你总是可以到达数组的最后一个位置。
解题思路
本题考查的是贪心思想。一开始我采取的贪心策略是:每次在跳跃的时候,都选择可跳跃范围内数组的最大值。
例如[2,3,1,1,2,4,1,3],数组起始位置对应的值为2,代表着下一次可跳跃范围为(3,1),对应的数组下标为(1,2),在可跳跃范围内选择对应数组的最大值也就是选择(3,1)中的最大值3。
采用这种策略能过一半的用例,但是当用例为[10,9,8,7,6,5,4,3,2,1,1,0]时,该贪心策略失败。
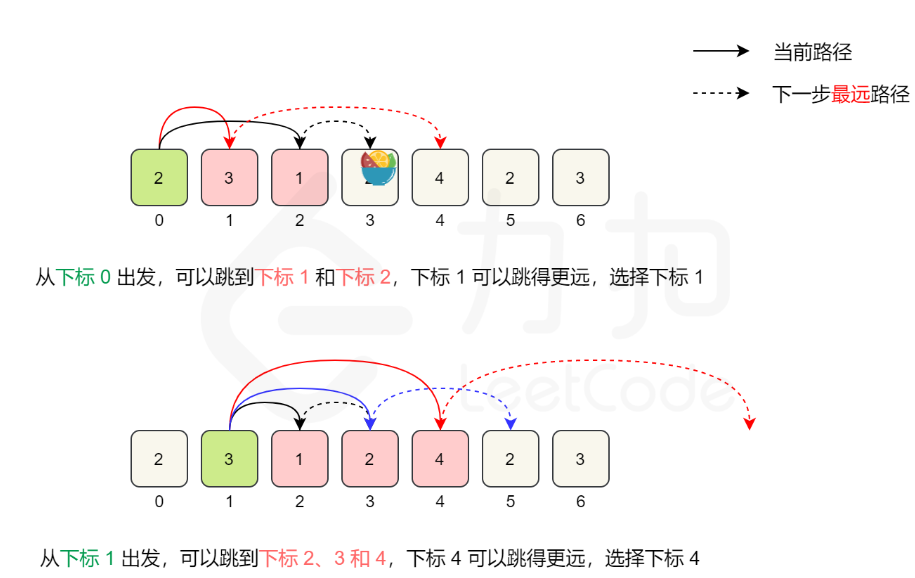
正确的贪心策略是:每次在跳跃的时候,都选择可跳跃范围内下一次可跳跃最远距离的点。
绿色框为当前位置,粉色框为可跳跃范围。
AC代码
1 class Solution { 2 public: 3 int jump(vector<int>& nums) { 4 int ans = 0; 5 int temp = 0; 6 if(nums.size() == 1) return 0; //6-7行代码是两个特例,我是先完成8-29行代码之后,才添加的两个特例,否则不能AC。 7 if(nums[0] >= nums.size() - 1) return 1; 8 for(int i = 0; i < nums.size(); ) 9 { 10 int len = INT_MIN; 11 for(int j = i; j < nums.size() && j <= i + nums[i]; j++) //11-18行代码就是进行下一次可达最远距离进行的求解。 12 { 13 if(nums[j]+j > len) 14 { 15 len = nums[j]+j; 16 temp = j; 17 } 18 } 19 i = temp; 20 ans++; 21 if(len >= nums.size() - 1) 22 { 23 ans++; 24 break; 25 } 26 } 27 return ans; 28 } 29 };
虽然说利用了双重for循环,但是其时间复杂度为O(n),空间复杂度为O(1)。
代码经过优化后,利用一个for循环即可。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
1 class Solution { 2 public: 3 int jump(vector<int>& nums) { 4 int step = 0; 5 int end = 0; 6 int maxlen = INT_MIN; 7 for(int i = 0; i < nums.size() - 1; i++) 8 { 9 maxlen = max(maxlen,nums[i]+i); 10 if(i == end) 11 { 12 step++; 13 end = maxlen; 14 } 15 } 16 return step; 17 } 18 };



 浙公网安备 33010602011771号
浙公网安备 33010602011771号