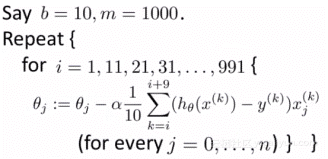李宏毅机器学习笔记2:Gradient Descent(附带详细的原理推导过程)
李宏毅老师的机器学习课程和吴恩达老师的机器学习课程都是都是ML和DL非常好的入门资料,在YouTube、网易云课堂、B站都能观看到相应的课程视频,接下来这一系列的博客我都将记录老师上课的笔记以及自己对这些知识内容的理解与补充。(本笔记配合李宏毅老师的视频一起使用效果更佳!)
梯度下降法(Gradient Descent)推导和示例(从另一个角度理解梯度下降算法,必看!)
今天这篇文章的主要内容是第3课的笔记
ML Lecture 3: Gradient Descent
1.要真正理解梯度下降算法的原理需要一定的数学功底、比如微积分、泰勒展开式等等......本文将从一个下山的场景开始,先提出梯度下降算法的基本思想,进而从数学上解释梯度下降算法的原理,
2.梯度下降的场景假设:梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率(即学习率),来确保下山的方向不错误,同时又不至于耗时太多!
4.大致理解了梯度下降之后,接下来让我们回到老师的PPT
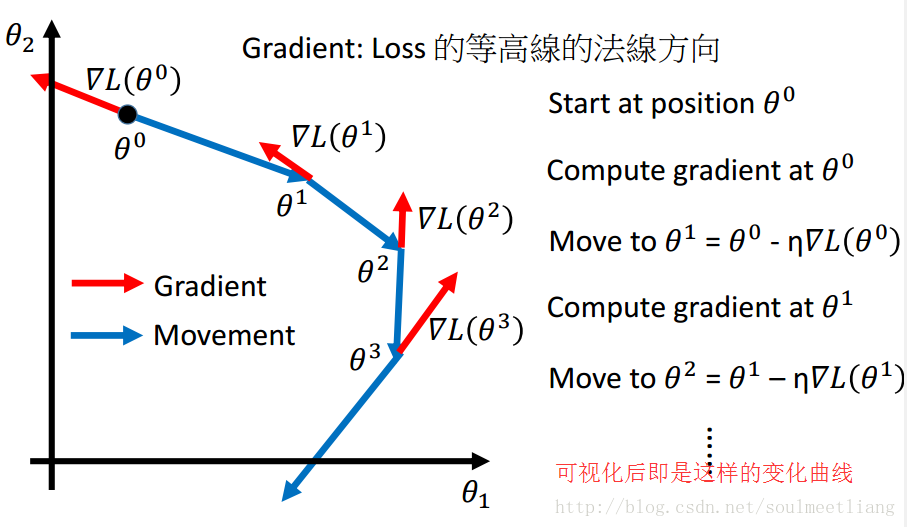
看到这可能有些人有这样的疑惑:为什么梯度下降的公式中间是减号而不是加号呢?接下来通过一张图片你就会理解了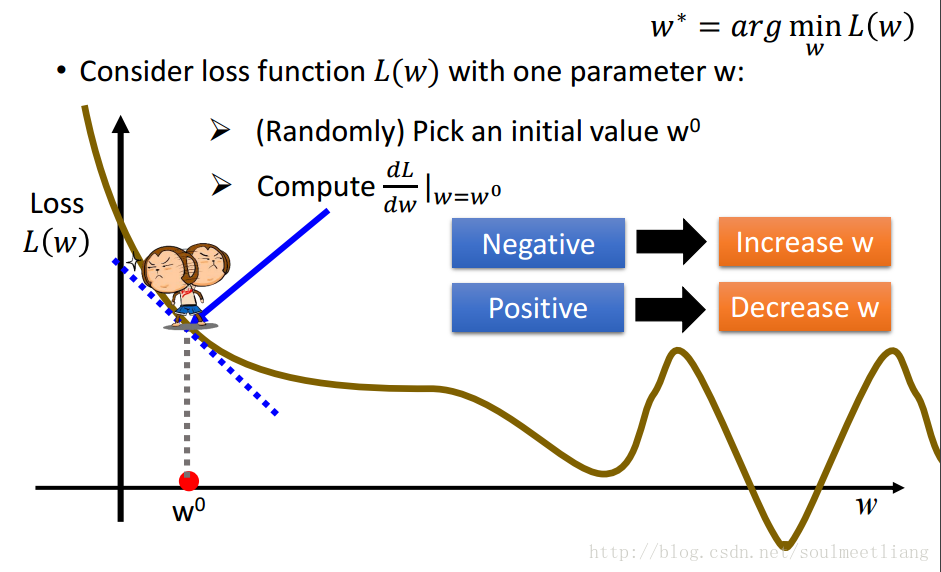
假设现在我们处在小猴子的问题,通过求导我们可以轻而易举的画出蓝色的切线,切线的斜率即为梯度值,根据图片可以知道,要是小猴子想达到最低点,就必须往W轴正方向移动,也就是增大W的值,而根据切线的方向可是知道该值为负,所以要想使W变大就必须使用负号,负负得正。
5.梯度下降的三个技巧
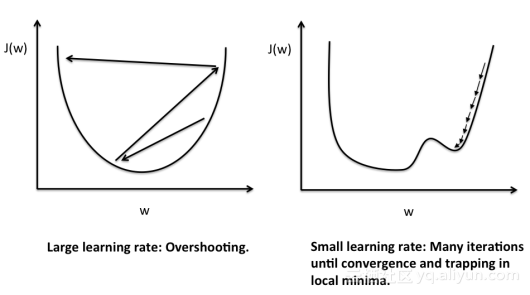
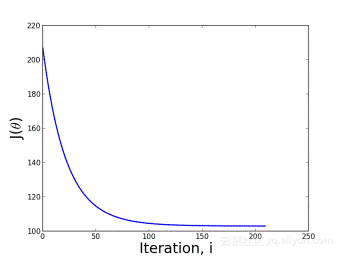
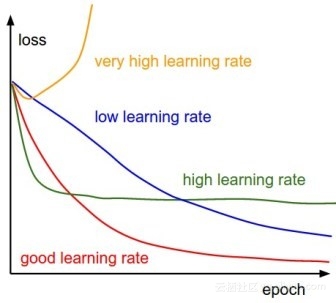
(1)Tuning your learning rates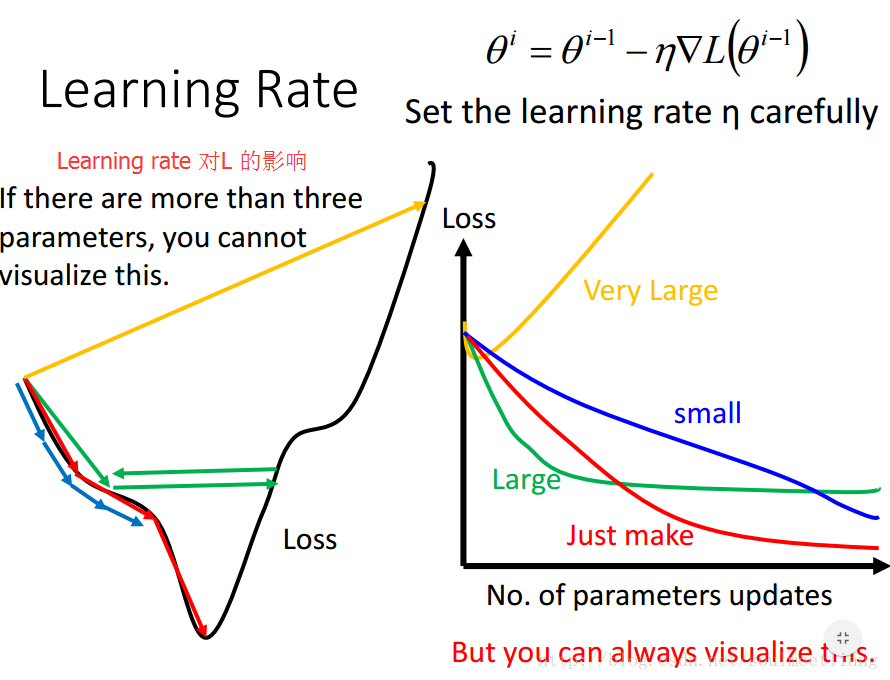
从图中可以看出学习率对梯度下降的影响力还是比较大的。在用梯度下降时最好画出loss随更新参数次数的曲线(如图),看一下前几次更新参数时曲线的走法如何。 如何做到调整学习率呢?其中一个思路是:每几个epoch之后就降低学习率(一开始离目标远,所以学习率大些,后来离目标近,学习率就小些),并且不同的参数有不同的学习率。接下来就让我们学习梯度下降中的一个方法Adagrad。
这样操作后,每组参数的learning rate 都不同。
举个例子帮助大家更好的理解: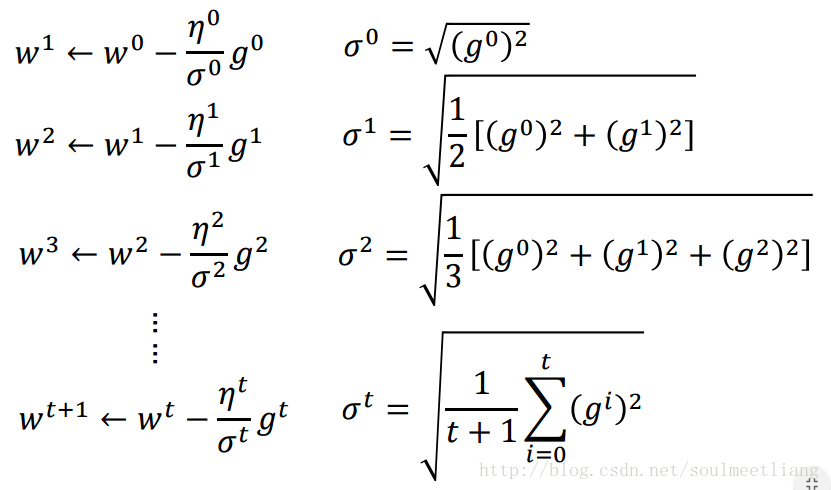
通过Adagrad后,我们的参数变化或者梯度下降公式可改写为: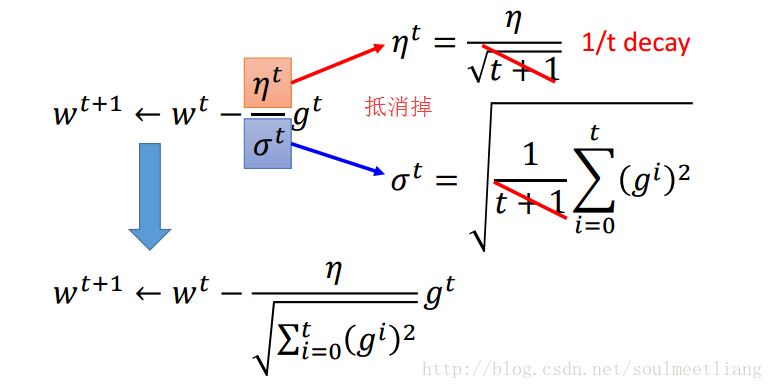
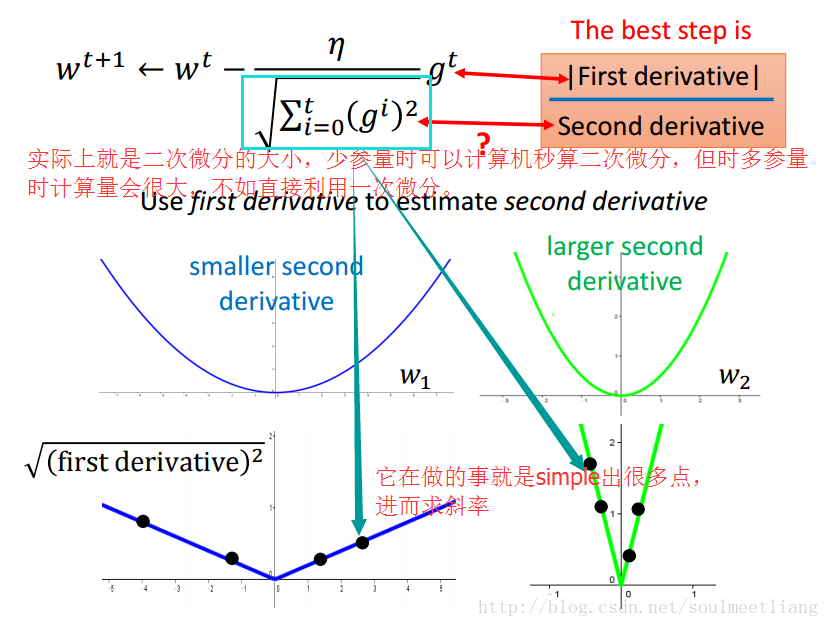
如何理解Adagrad的参数更新式子呢?(以一元二次函数为例)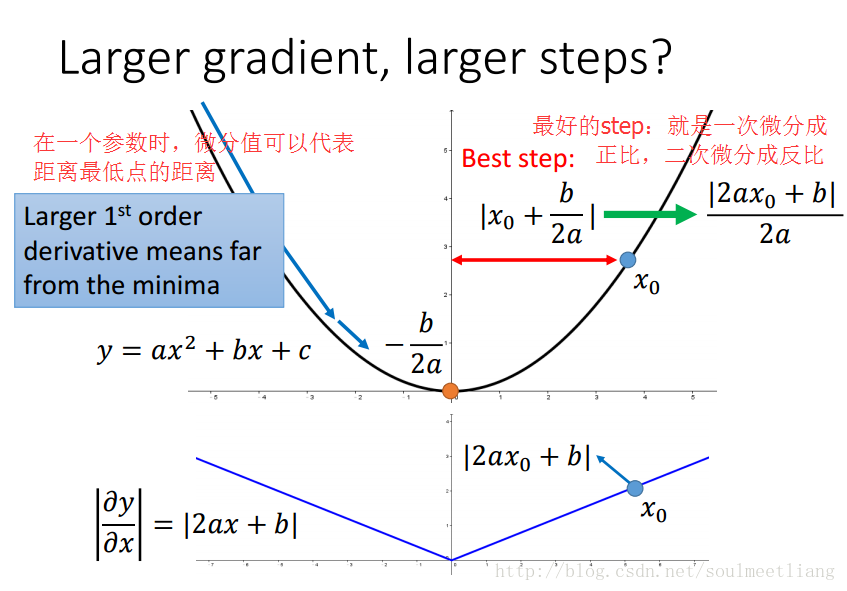
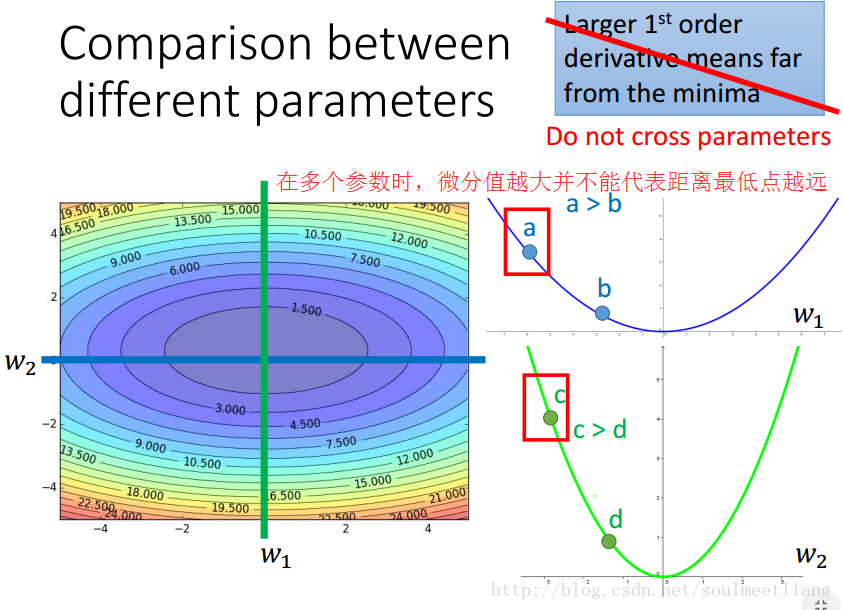
(2)Stochastic Gradient Descent(SGD)
SGD让训练过程更快。普通GD是在看到所有样本(训练数据)之后,计算出损失L,再更新参数。而SGD是每看到一个样本就计算出一个损失,然后就更新一次参数。
(3)Feature Scaling
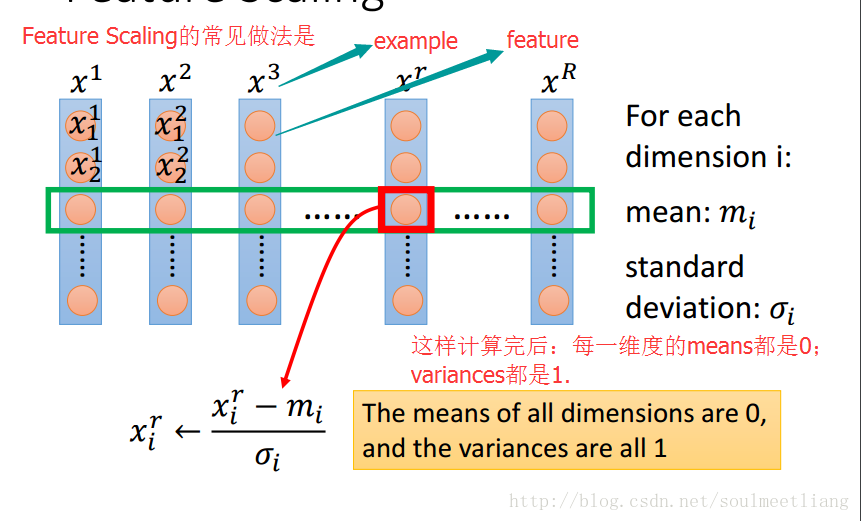
如果不同参数的取值范围大小不同,那么loss函数等高线方向(负梯度方向,参数更新方向)不指向loss最低点。feature scaling让不同参数的取值范围是相同的区间,这样loss函数等高线是一系列共圆心的正圆,更新参数更容易。 feature scaling的做法是,把input feature的每个维度都标准化(减去该维度特征的均值,除以该维度的标准差)。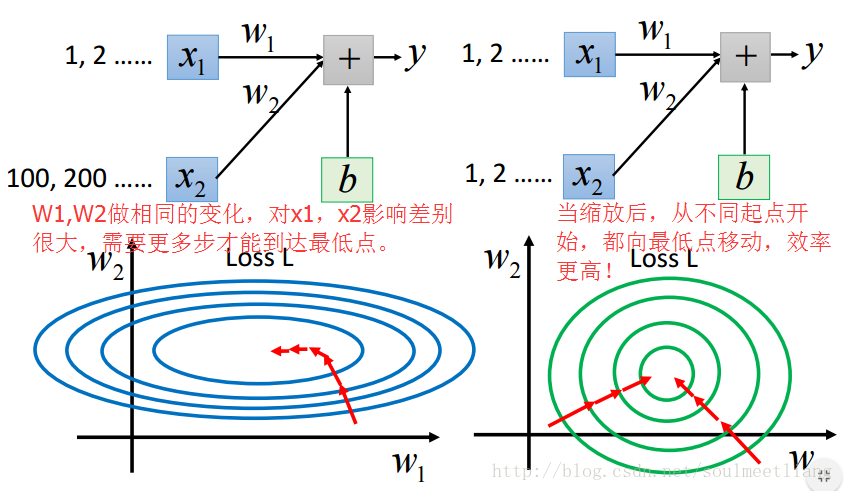
6.高能预警:梯度下降算法的原理!(需要一定的数学功底,比如微积分、泰勒展开式)
(1)如下图所示,整个平面表示一个损失函数,要求整个平面的最小值,可以把这个问题分解成随机给定一点和一个很小的范围,求出这个范围内的最小值,然后在以这个最小值为中心点,结合给定的小范围反复求解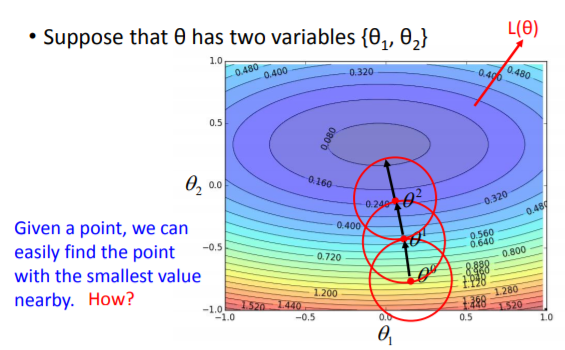
(2)如何求出一个指定很小范围内的最小值呢?这就需要用到泰勒级数了。
(3)当有两个变量的时候,泰勒级数变为:

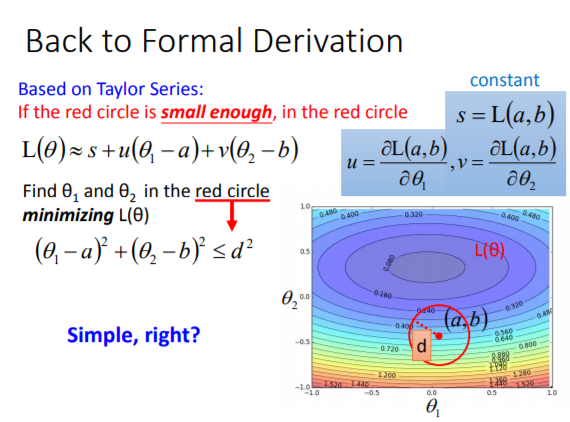
(5)如下图所示:因为要求最小值且s为常量,所以可以先忽略s的影响,所以损失函数的计算就变为了两个向量之间的乘法,且其中向量(u,v)的方向和大小是已知的,当(theta1,theta2)与(u,v)反向的时候,两个向量相乘的结果最小。又因为是在一个以(theta1,theta2)为圆心的小范围内,所以可以在(theta1,theta2)之前乘上一个值,让这个向量的长度正好等于这个小圆的半径,这样我们就求出了损失函数的最小值。


(6)经过这个推导的过程,想必大家也都能明白为什么在梯度下降中的学习率不能太大。因为,若要满足梯度下降的表达式,就必须要满足泰勒级数,而我们只取泰勒级数前两项的条件是x必须非常接近x0,也就是说我们的那个红色的圆的半径必须足够小,因为(theta1,theta2)*学习率=圆的半径,既然圆的半径必须要足够小,所以推导除了学习率正比与圆的半径,也要足够小!
(1)局部最小值
到目前为止来说,梯度下降看起来是一个非常美好的童话。不过我要开始泼凉水了。还记得我之前说过,我们的损失函数是一个非常好的函数,这样的损失函数并不真的存在?我们以神经网络为例,神经网络是复杂函数,具有大量非线性变换。由此得到的损失函数看起来不像一个很好的碗,只有一处最小值可以收敛。实际上,这种圣人般的损失函数称为凸函数,而深度网络的损失函数几乎总是非凸的事实上,损失函数可能是这样的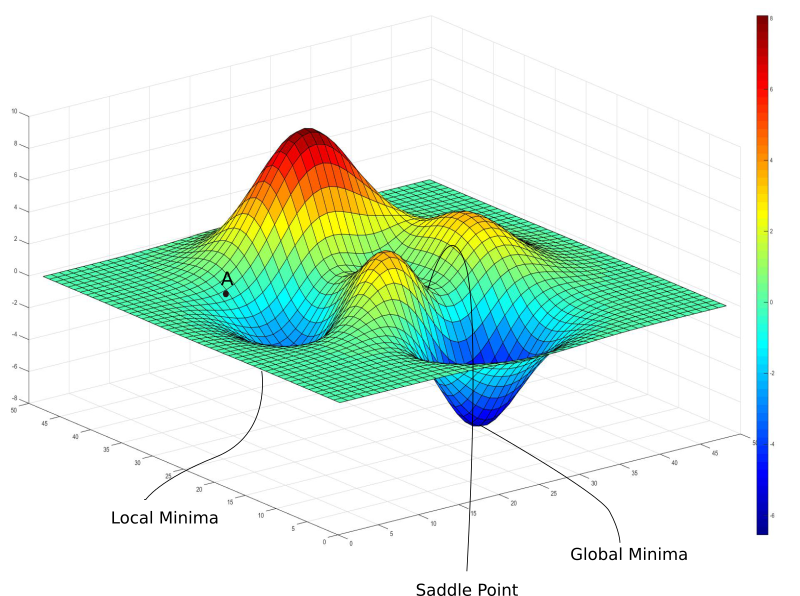
上图中有一个梯度为零的局部极小值。然而,我们知道那不是我们能达到的最低损失(全局最小值)。如果初始权重位于点A,那么我们将收敛于局部极小值,一旦收敛于局部极小值,梯度下降无法逃离这一陷阱。梯度下降是由梯度驱动的,而梯度在任何极小值处都是零。局部极小值,顾名思义,是损失函数在局部达到最小值的点。而全局最小值,是损失函数整个定义域上可以达到的最小值。让事情更糟的是,损失等值曲面可能更加复杂,实践中可没有我们考虑的三维等值曲面。实践中的神经网络可能有上亿权重,相应地,损失函数有上亿维度。在那样的图像上梯度为零的点不知道有多少。
(2)鞍点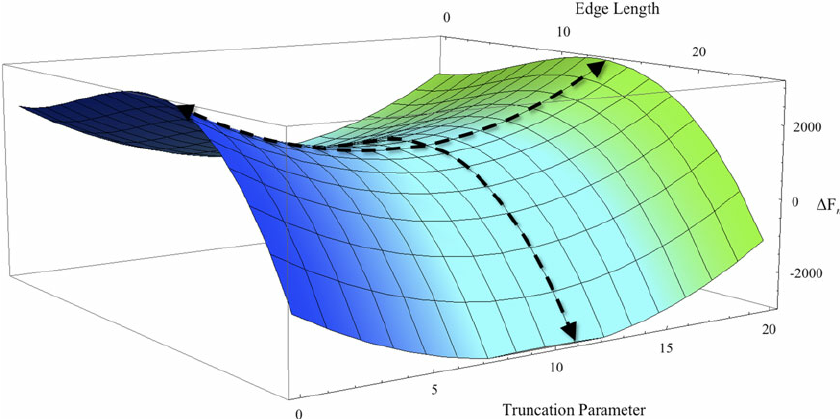
鞍点因形状像马鞍而得名。鞍点处,梯度在一个方向(X)上是极小值,在另一个方向上则是极大值。如果沿着X方向的等值曲面比较平,那么梯度下降会沿着Ÿ方向来回振荡,造成收敛于最小值的错觉。
以上就是本节课所学和理解的知识点,欢迎大家指正!
梯度下降法 (Gradient Descent Algorithm,GD) 是为目标函数J(θ),如代价函数(cost function), 求解全局最小值(Global Minimum)的一种迭代算法。
为什么使用梯度下降法
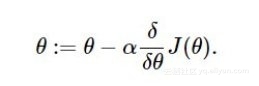
α表示学习速率(learning rate)。
梯度下降法的工作原理
梯度下降法的类型
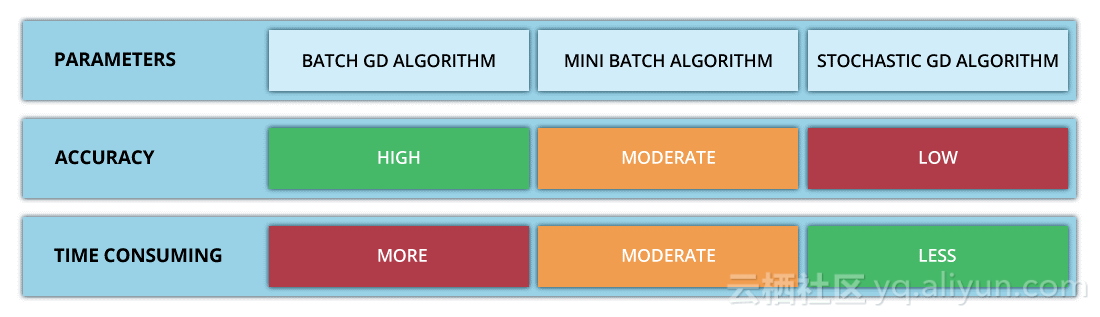
基于如何使用数据计算代价函数的导数,梯度下降法可以被定义为不同的形式(various variants)。确切地说,根据使用数据量的大小(the amount of data),时间复杂度(time complexity)和算法的准确率(accuracy of the algorithm),梯度下降法可分为:
1. 批量梯度下降法(Batch Gradient Descent, BGD);
2. 随机梯度下降法(Stochastic Gradient Descent, SGD);
3. 小批量梯度下降法(Mini-Batch Gradient Descent, MBGD)。
批量梯度下降法原理
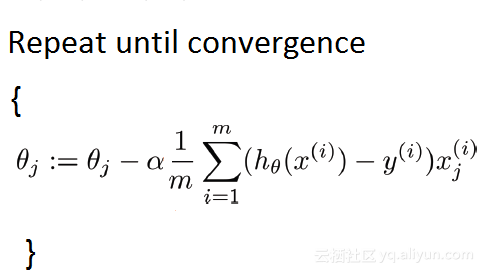
其中,m是训练样本(training examples)的数量。
Note:
1. 如果训练集有3亿条数据,你需要从硬盘读取全部数据到内存中;
2. 每次一次计算完求和后,就进行参数更新;
3. 然后重复上面每一步;
4. 这意味着需要较长的时间才能收敛;
5. 特别是因为磁盘输入/输出(disk I/O)是系统典型瓶颈,所以这种方法会不可避免地需要大量的读取。
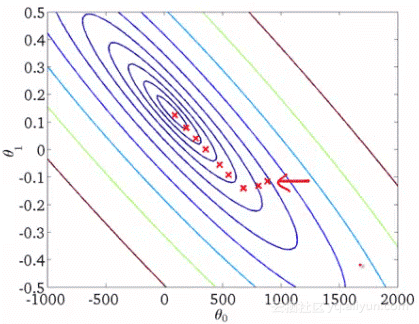
上图是每次迭代后的等高线图,每个不同颜色的线表示代价函数不同的值。运用梯度下降会快速收敛到圆心,即唯一的一个全局最小值。批量梯度下降法不适合大数据集。
随机梯度下降法原理

这里m表示训练样本的数量。
如下为随机梯度下降法的伪码:
1. 进入内循环(inner loop);
2. 第一步:挑选第一个训练样本并更新参数,然后使用第二个实例;
3. 第二步:选第二个训练样本,继续更新参数;
4. 然后进行第三步…直到第n步;
5. 直到达到全局最小值
如下图所示,随机梯度下降法不像批量梯度下降法那样收敛,而是游走到接近全局最小值的区域终止。
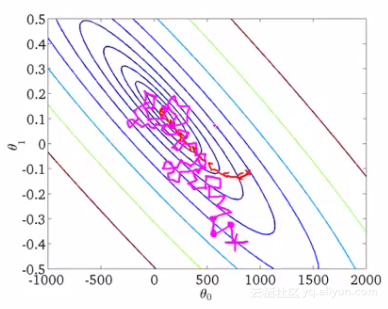
小批量梯度下降法原理
小批量梯度下降法是最广泛使用的一种算法,该算法每次使用m个训练样本(称之为一批)进行训练,能够更快得出准确的答案。小批量梯度下降法不是使用完整数据集,在每次迭代中仅使用m个训练样本去计算代价函数的梯度。一般小批量梯度下降法所选取的样本数量在50到256个之间,视具体应用而定。
1.这种方法减少了参数更新时的变化,能够更加稳定地收敛。
2.同时,也能利用高度优化的矩阵,进行高效的梯度计算。
随机初始化参数后,按如下伪码计算代价函数的梯度: