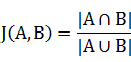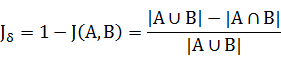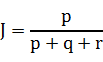句子相似度-编辑距离、余弦距离、杰卡德相似性

参考：http://www.cnblogs.com/biyeymyhjob/archive/2012/09/28/2707343.html
http://www.cnblogs.com/pandora/archive/2009/12/20/levenshtein_distance.html

 

简介与描述：

编辑距离，又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

例如将kitten一字转成sitting：

1. sitten （k→s）
2. sittin （e→i）
3. sitting （→g）

俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。

 

问题：找出字符串的编辑距离，即把一个字符串s1最少经过多少步操作变成编程字符串s2，操作有三种，添加一个字符，删除一个字符，修改一个字符

 

解析：

首先定义这样一个函数——edit(i, j)，它表示第一个字符串的长度为i的子串到第二个字符串的长度为j的子串的编辑距离。

显然可以有如下动态规划公式：

• if i == 0 且 j == 0，edit(i, j) = 0
• if i == 0 且 j > 0，edit(i, j) = j
• if i > 0 且j == 0，edit(i, j) = i
• if i ≥ 1  且 j ≥ 1 ，edit(i, j) == min{ edit(i-1, j) + 1, edit(i, j-1) + 1, edit(i-1, j-1) + f(i, j) }，当第一个字符串的第i个字符不等于第二个字符串的第j个字符时，f(i, j) = 1；否则，f(i, j) = 0。

     

 

计算编辑距离PYthon版

# -*- coding: utf-8 -*-

def distacal(s1,s2):#计算编辑距离
    m = len(s1)
    n = len(s2)
    colsize, matrix = m + 1, []
    for i in range((m + 1) * (n + 1)):
        matrix.append(0)
    for i in range(colsize):
        matrix[i] = i
    for i in range(n + 1):
        matrix[i * colsize] = i
    for i in range(n + 1)[1:n + 1]:
        for j in range(m + 1)[1:m + 1]:
            if s1[j - 1] == s2[i - 1]:
                cost = 0
            else:
                cost = 1
            minValue = matrix[(i - 1) * colsize + j] + 1
            if minValue > matrix[i * colsize + j - 1] + 1:
                minValue = matrix[i * colsize + j - 1] + 1
            if minValue > matrix[(i - 1) * colsize + j - 1] + cost:
                minValue = matrix[(i - 1) * colsize + j - 1] + cost
            matrix[i * colsize + j] = minValue
    return matrix[n * colsize + m]
    

distance = distacal("你说你是谁","我不知道你是谁")
print distance

程序（C++）：注意二维数组动态分配和释放的方法！！

#include <iostream>
#include <string>

using namespace std;

int min(int a, int b)
{
    return a < b ? a : b;
}

int edit(string str1, string str2)
{
    int max1 = str1.size();
    int max2 = str2.size();

    int **ptr = new int*[max1 + 1];
    for(int i = 0; i < max1 + 1 ;i++)
    {
        ptr[i] = new int[max2 + 1];
    }

    for(int i = 0 ;i < max1 + 1 ;i++)
    {
        ptr[i][0] = i;
    }

    for(int i = 0 ;i < max2 + 1;i++)
    {
        ptr[0][i] = i;
    }

    for(int i = 1 ;i < max1 + 1 ;i++)
    {
        for(int j = 1 ;j< max2 + 1; j++)
        {
            int d;
            int temp = min(ptr[i-1][j] + 1, ptr[i][j-1] + 1);
            if(str1[i-1] == str2[j-1])
            {
                d = 0 ;
            }
            else
            {
                d = 1 ;
            }
            ptr[i][j] = min(temp, ptr[i-1][j-1] + d);
        }
    }

    cout << "**************************" << endl;
    for(int i = 0 ;i < max1 + 1 ;i++)
    {
        for(int j = 0; j< max2 + 1; j++)
        {
            cout << ptr[i][j] << " " ;
        }
        cout << endl;
    }
    cout << "**************************" << endl;
    int dis = ptr[max1][max2];

    for(int i = 0; i < max1 + 1; i++)
    {
        delete[] ptr[i];
        ptr[i] = NULL;
    }

    delete[] ptr;
    ptr = NULL;

    return dis;
}

int main(void)
{
    string str1 = "sailn";
    string str2 = "failing";

    int r = edit(str1, str2);
    cout << "the dis is : " << r << endl;

    return 0;
}

 

可能进行的改进

• 现在的算法复杂度为O(mn)，可以将其改进为O(m)。因为这个算法只需要上一行和当前行被存储下来就可以了。
• 如果需要重现转换步骤，我们可以把每一步的位置和所进行的操作保存下来，进行重现。
• 如果我们只需要比较转换步骤是否小于一个特定常数k，那么只计算高宽宽为2k+1的矩形就可以了，这样的话，算法复杂度可简化为O(kl)，l代表参加对比的最短string的长度。
• 我们可以对三种操作（添加，删除，替换）给予不同的权值（当前算法均假设为1，我们可以设添加为1，删除为0，替换为2之类的），来细化我们的对比。
• 如果我们将第一行的所有cell初始化为0，则此算法可以用作模糊字符查询。我们可以得到最匹配此字符串的字符串的最后一个字符的位置（index number），如果我们需要此字符串的起始位置，我们则需要存储各个操作的步骤，然后通过算法计算出字符串的起始位置。
• 这个算法不支持并行计算，在处理超大字符串的时候会无法利用到并行计算的好处。但我们也可以并行的计算cost values（两个相同位置的字符是否相等），然后通过此算法来进行整体计算。
• 如果只检查对角线而不是检查整行，并且使用延迟验证（lazy evaluation），此算法的时间复杂度可优化为O(m(1+d))（d代表结果）。这在两个字符串非常相似的情况下可以使对比速度速度大为增加。

 

参考：http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html

第一步，分词。

　　句子A：我/喜欢/看/电视，不/喜欢/看/电影。

　　句子B：我/不/喜欢/看/电视，也/不/喜欢/看/电影。

第二步，列出所有的词。

　　我，喜欢，看，电视，电影，不，也。

第三步，计算词频。

　　句子A：我 1，喜欢 2，看 2，电视 1，电影 1，不 1，也 0。

　　句子B：我 1，喜欢 2，看 2，电视 1，电影 1，不 2，也 1。

第四步，写出词频向量。

　　句子A：[1, 2, 2, 1, 1, 1, 0]

　　句子B：[1, 2, 2, 1, 1, 2, 1]

 

假定A和B是两个n维向量，A是 [A1, A2, ..., An] ，B是 [B1, B2, ..., Bn] ，则A与B的夹角θ的余弦等于：

 

因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

 

参考：
        http://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html

 

3、杰卡德相似性度量

（1）杰卡德相似系数

两个集合A和B交集元素的个数在A、B并集中所占的比例，称为这两个集合的杰卡德系数，用符号 J(A,B) 表示。杰卡德相似系数是衡量两个集合相似度的一种指标（余弦距离也可以用来衡量两个集合的相似度）。

（2）杰卡德距离

与杰卡德相似系数相反的概念是杰卡德距离（Jaccard Distance），可以用如下公式来表示：

杰卡德距离用两个两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

（3）杰卡德相似系数的应用

假设样本A和样本B是两个n维向量，而且所有维度的取值都是0或1。例如，A（0,1,1,0）和B（1,0,1,1）。我们将样本看成一个集合，1表示集合包含该元素，0表示集合不包含该元素。

p：样本A与B都是1的维度的个数

q：样本A是1而B是0的维度的个数

r：样本A是0而B是1的维度的个数

s：样本A与B都是0的维度的个数

那么样本A与B的杰卡德相似系数可以表示为：

此处分母之所以不加s的原因在于：

对于杰卡德相似系数或杰卡德距离来说，它处理的都是非对称二元变量。非对称的意思是指状态的两个输出不是同等重要的，例如，疾病检查的阳性和阴性结果。

按照惯例，我们将比较重要的输出结果，通常也是出现几率较小的结果编码为1（例如HIV阳性），而将另一种结果编码为0（例如HIV阴性）。给定两个非对称二元变量，两个都取1的情况（正匹配）认为比两个都取0的情况（负匹配）更有意义。负匹配的数量s认为是不重要的，因此在计算时忽略。

（4）杰卡德相似度算法分析

杰卡德相似度算法没有考虑向量中潜在数值的大小，而是简单的处理为0和1，不过，做了这样的处理之后，杰卡德方法的计算效率肯定是比较高的，毕竟只需要做集合操作。