poj 1611 The Suspects（第一道并查集）

 

题意：

　　有N个学生，编号为0-n-1，现在0号学生感染了非典，凡是和0在一个社团的人就会感染，

并且这些人如果还参加了别的社团，他所在的社团照样全部感染，社团个数为m，求感染的人数。

输入：

　　n代表人数，m代表社团数

　　社团的人数，第一个人编号，……

　　……

#include<stdio.h>
const int MAX=30000;
int n,m,k;
int parent[MAX+10];
int total[MAX+10];
//total[GetParent(a)] 是a所在的group的人数
int GetParent(int a)
{//获取a的根，并把a的父节点改为跟
    if(parent[a]!=a)
        parent[a]=GetParent(parent[a]);
    return parent[a];
}
void Merge(int a,int b)
{
    int p1=GetParent(a);
    int p2=GetParent(b);
    if(p1==p2)
        return ;
    total[p1]+=total[p2];
    parent[p2]=p1;
}
int main()
{
    int i,j;
    while(true)
    {
        scanf("%d%d",&n,&m);
        if(n==0&&m==0)break;
        for(i=0;i<n;i++)
        {
            parent[i]=i;
            total[i]=1;
        }
        for(i=0;i<m;i++)
        {
            int h,s;
            scanf("%d%d",&k,&h);
            for(j=1;j<k;j++)
            {
                scanf("%d",&s);
                Merge(h,s);
            }
        }
        printf("%d\n",total[GetParent(0)]);;
    }
    return 0;
}

 

 

摘自：Jack Ge for ACM
http://www.cnblogs.com/jackge/archive/2013/04/17/3027238.html

并查集学习：

l         并查集：(union-find sets)

一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多，如其求无向图的连通分量个数等。最完美的应用当属：实现Kruskar算法求最小生成树。

l         并查集的精髓（即它的三种操作，结合实现代码模板进行理解）：

1、MakeSet(x) 把每一个元素初始化为一个集合

初始化后每一个元素的父亲节点是它本身，每一个元素的祖先节点也是它本身（也可以根据情况而变）。

2、FindSet(x) 查找一个元素所在的集合

查找一个元素所在的集合，其精髓是找到这个元素所在集合的祖先！这个才是并查集判断和合并的最终依据。
判断两个元素是否属于同一集合，只要看他们所在集合的祖先是否相同即可。
合并两个集合，也是使一个集合的祖先成为另一个集合的祖先，具体见示意图

3、Union(x,y) 合并x,y所在的两个集合

合并两个不相交集合操作很简单：
利用Find_Set找到其中两个集合的祖先，将一个集合的祖先指向另一个集合的祖先。如图

     

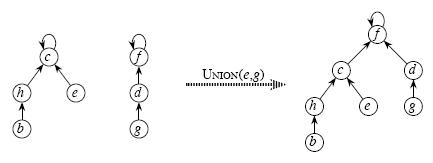
l         并查集的优化

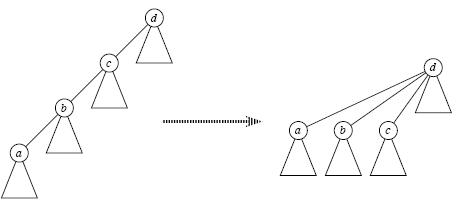
　　路径压缩
　　FindSet(x)寻找祖先时我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度，有没有办法减小这个复杂度呢？
答案是肯定的，这就是路径压缩，即当我们经过"递推"找到祖先节点后，"回溯"的时候顺便将它的子孙节点都直接指向祖先，这样以后再次Find_Set(x)时复杂度就变成O(1)了，Union(x,y)
即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。路径压缩方便了以后的查找。

     

#include<stdio.h>
const int maxn=30010;
int father[maxn];
int total[maxn];
void MakeSet(int n)
{
    for(int i=0; i<n; i++)
    {
        father[i]=i;
        total[i]=1;
    }
}
int FindSet(int x)
{
    if(x!=father[x])
        father[x]=FindSet(father[x]);
    return father[x];
}
void Union(int a,int b)
{
    int x=FindSet(a);
    int y=FindSet(b);
    if(x==y)
        return ;
    if(total[x]>=total[y])
    {
        father[y]=x;
        total[x]+=total[y];
    }
    else
    {
        father[x]=y;
        total[y]+=total[x];
    }
}
int main()
{
    int n,m;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        if(n==0&&m==0)
            break;
        int k,a,b;
        MakeSet(n);
        while(m--)
        {
            scanf("%d %d",&k,&a);
            for(int i=1; i<k; i++)
            {
                scanf("%d",&b);
                Union(a,b);
            }
        }
        printf("%d\n",total[father[0]]);
    }
    return 0;
}