【DDSCAT——离散偶极近似仿真程序11】DDSCAT目标方向的调整
这一部分我们研究一下对DDSCAT目标模型在坐标系中的角度调整问题。
先来看一波手册原文:
Every target is defined by a list of “occupied” lattice sites (i; j; k)n, n = 1; :::; N. In the “Target Frame” (TF), these sites have physical locations (x; y; z)n = [(i; j; k)n + (x0; y0; z0)] × d, where d is the lattice constant (in physical units) and (x0; y0; z0) is a vector that gives the physical location corresponding to (i; j; k) = (0; 0; 0).
这个TF,目标架构,我理解的就是通过我们shape.dat或target.out文件中设定的每个偶极子点的坐标来表示目标整体位置的坐标系。
TF也就是以目标自身为主的坐标系。
------------------------------------------------------------------------------------------------------------------------
Recall that we define a “Lab Frame” (LF) in which the incident radiation propagates in the +x direction. For purposes of discussion we will always let unit vectors x^LF, y^LF, z^LF = x^LF × y^LF be the three coordinate axes of the LF.
DDSCAT又定义了一个Lab架构,其中,入射光需沿x轴正方向传播。而x^LF, y^LF, z^LF = x^LF × y^LF分别为这个坐标系的三个坐标轴。这个LF,我们就理解为常见的笛卡尔坐标系,而特殊的地方就是,LF规定了入射光必须沿+x方向传播。
LF也就是以入射光为主的坐标系。
--------------------------------------------------------------------------------------------------------------------------
Recall that definition of a target involves specifying two unit vectors, a^1 and a^2, which are imagined to be “frozen” into the target. We require a^2 to be orthogonal to a^1. Therefore we may define a “Target Frame" (TF) defined by the three unit vectors a^1, a^2, and a^3 = a^1 × a^2 .
a^1 和 a^2 是冻结(固定)在目标中的两个正交向量,这两个向量是用来表示目标方向的。如果再需要一个a^3,则a^3 = a^1 × a^2。
-----------------------------------------------------------------------------------------------------------------------------
Orientation of the target relative to the incident radiation can in principle be determined two ways:
1. specifying the direction of a^1 and a^2 in the LF, or
2. specifying the directions of x^LF (incidence direction) and y^LF in the TF.
相对于入射光方向,目标的方向原则上可以被一下两种方式确定:
1. 指定LF中 a^1 和 a^2 的方向(也就LF静止,目标是动态的,即LF作为参考系);
2. 指定TF中 x^LF(入射方向)和 y^LF 的方向(也就是目标静止,入射光是动态的,即TF作为参考系)。
--------------------------------------------------------------------------------------------------------------------------------
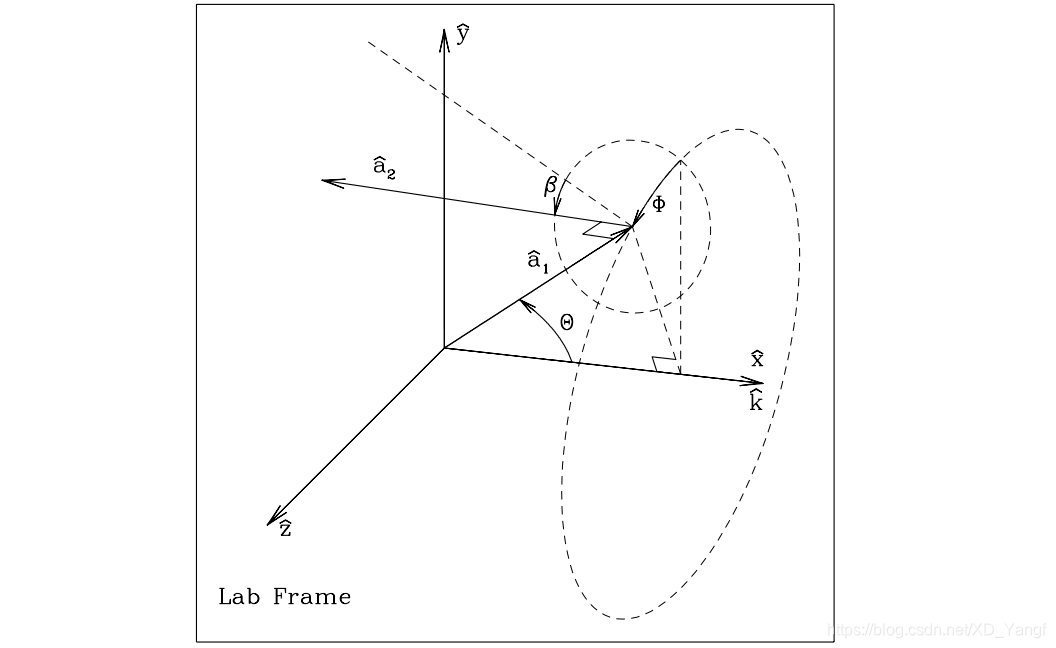
DDSCAT uses method 1.: the angles Θ, Φ, and β are specified in the file ddscat.par. The target is oriented such that the polar angles Θ and Φ specify the direction of a^1 relative to the incident direction x^LF, where the x^LF,y^LF plane has Φ = 0. Once the direction of a^1 is specified, the angle β then specifies how the target is to rotated around the axis a^1 to fully specify its orientation.
DDSCAT选择了使用方法1,则需要在ddscat.par中设定Θ, Φ, 和 β这三个角度来确定目标的方向。Θ和Φ指定了 a^1 相对于入射方向 x^LF 的方向,如果Φ = 0,则 a^1 会在 x^LF,y^LF 平面内。固定了 a^1 的方向之后,β角制定了目标绕 a^1 轴如何旋转,从而可以完整的确定目标的方向。
这里我们多理解一下,看图可知,Θ 规定了a^1 和 x^LF 之间的角度,Φ 规定了 a^1 和 x^LF,y^LF 平面之间的角度,这样一来,以LF原点为起点的 a^1 向量的方向就被确定了。同时,也可以理解,Φ = 0 则表示 a^1 会在 x^LF,y^LF 平面内了。而 a^2 是与 a^1 相正交的另一个向量,且起点为 a^1 的重点,而 β 表示了 a^2 与 a^1, x^LF 平面之间的夹角,由此固定了 a^2 的方向。

接下来,我们就可以通过改变Θ, Φ, 和 β这三个角度来调整目标的方向了。
方法很简单,需要在ddscat.par里面设置下面这部分数值。
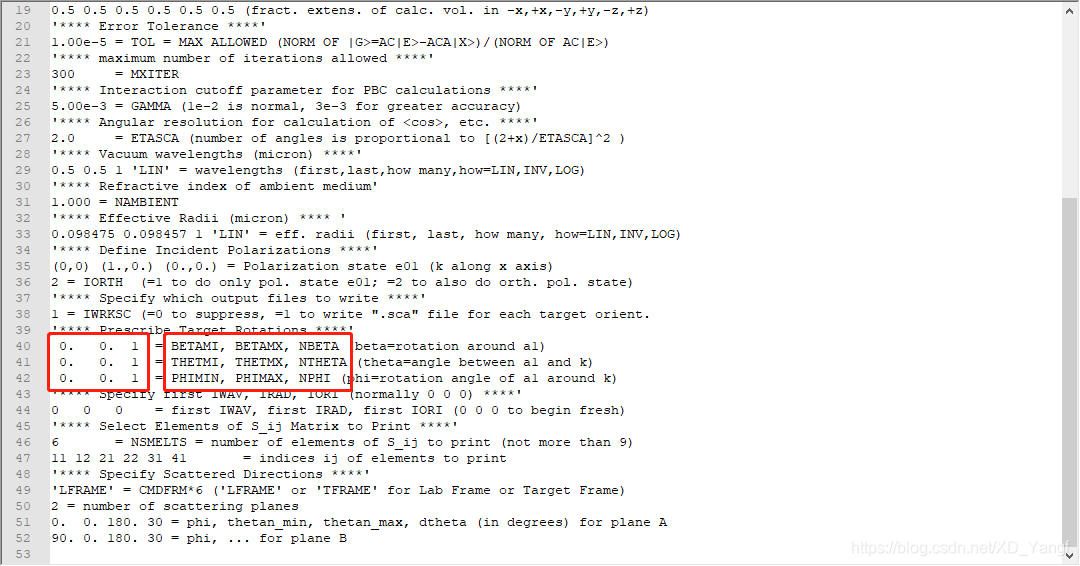
其中,每行的三个数分别表示改角度的首个值、末了值和角度的数量。
要注意的是,如果数量不是单个,则这里的角度分配方式,不是和前面的Vacuum wavelengths和Effective Radii的平均增长方式完全一样。我们需要先看下原文:
Note that when DDSCAT 7.3 chooses angles it handles β and Φ differently from Θ. The range for β is divided into NBETA intervals, and the midpoint of each interval is taken. Thus, if you take BETAMI=0, BETAMX=90, NBETA=2 you will get β = 22:5° and 67:5°. Similarly, if you take PHIMIN=0, PHIMAX=180, NPHI=2 you will get Φ = 45° and 135°.
β的角度分配方式为,先根据NBETA的值来将首尾值的区间进行划分,然后在取每个区间的中值为所有的 β 角度。
----------------------------------------------------------------------------------------------------------------------------
根据手册的意思,Φ的分配方式应该是和 β 相同的。
-----------------------------------------------------------------------------------------------------------------------------
Sampling in Θ is done quite differently from sampling in β and Φ. First, as already mentioned above, DDSCAT 7.3 samples uniformly in cos Θ, not Θ. Secondly, the sampling depends on whether NTHETA is even or odd.
• If NTHETA is odd, then the values of Θ selected include the extreme values THETMI and THETMX; thus, THETMI=0, THETMX=90, NTHETA=3 will give you Θ = 0°; 60°; 90°.
• If NTHETA is even, then the range of cos Θ will be divided into NTHETA intervals, and the midpoint of each interval will be taken; thus, THETMI=0, THETMX=90, NTHETA=2 will give you Θ = 41:41° and 75:52° [cos Θ = 0:25 and 0:75].
而Θ的分配方式最与众不同,首先,Θ是以cos Θ的方式平均的,即根据cos Θ对应的小数值分配。具体的分配方式还有奇偶之分。
• 如果NTHETA是奇数,则最终分配出的角度是包括预先设定的首尾值的,例如,若设定THETMI=0, THETMX=90, NTHETA=3,则能得到 Θ = 0; 60°; 90°。因为,0°和90°是首尾值,而NTHETA是奇数,则这两个角度必得到,而cos 60 = 0.5,则60°是第三个值。
• 如果NTHETA是偶数,则将cos Θ 的范围分为NTHETA个区间,然后取每个区间的中值,得出所有的 Θ 值。例如,若THETMI=0, THETMX=90, NTHETA=2,则可以得到Θ = 41:41° and 75:52° (因为,cos Θ = 0:25 和 0:75)。
以下的内容还在更新中。。。
一、调整THETA角
1)THETA = 0, 22.5, 45, 67.5, 90 degree PHI = 0, BETA = 0
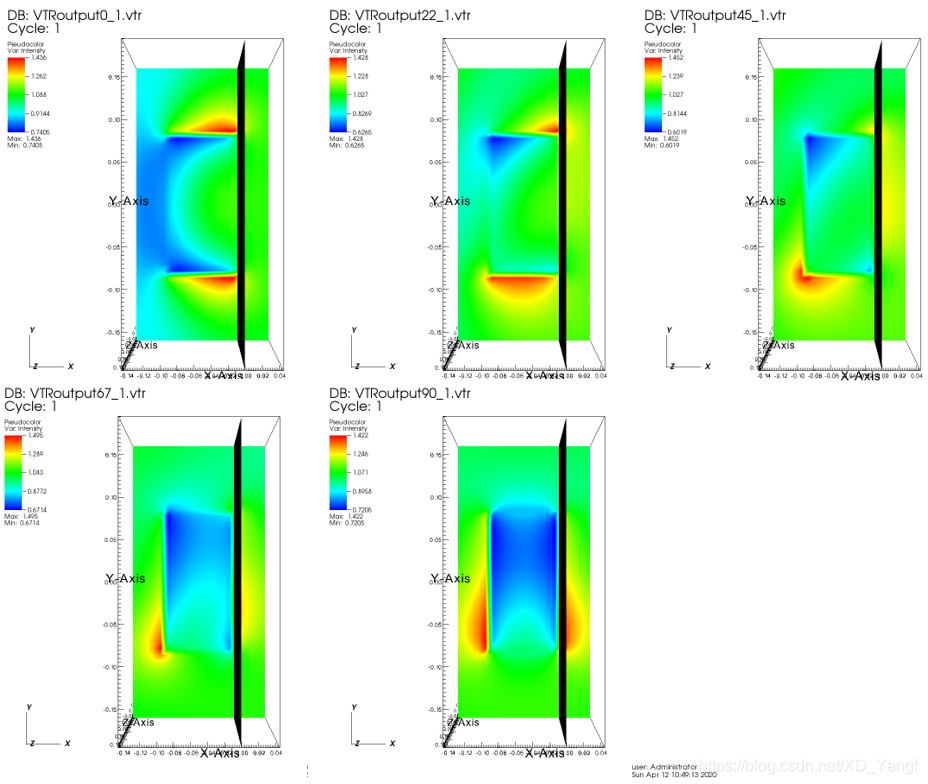
说好的改变了THETA角,目标应该绕着z轴旋转才对,怎么呈现出来的电场图没有转呢。
别急,我们仔细观察电场图,发现场强较强的红色黄色部分一开始是分布在模型上下两侧的。而后来,随着THETA角度的改变,场强强度分布有点变化,下强上弱。而到最后一张图的时候(THETA = 90 degree),发现,原本上下对称的场强,现在变得左右对称了。这时候,就验证了我们一开始的猜想:
DDSCAT计算出的场强模型,目标方向没有改变,而是入射光方向和极化方向相对改变了(极化方向也是两个正交的方向,其中,e^01与y轴平行,e^02与z轴平行;对于极化方向方面的概念,我目前也不是很清楚,以后看懂了再跟大家分享)。因此,如果我们想要看到转动的目标和固定的LF坐标系,就需要我们自己手动转动电场模型。
2) 调整角度之后(蓝色边框箭头表示模型旋转方向,此例中表示目标绕z轴逆时针旋转)
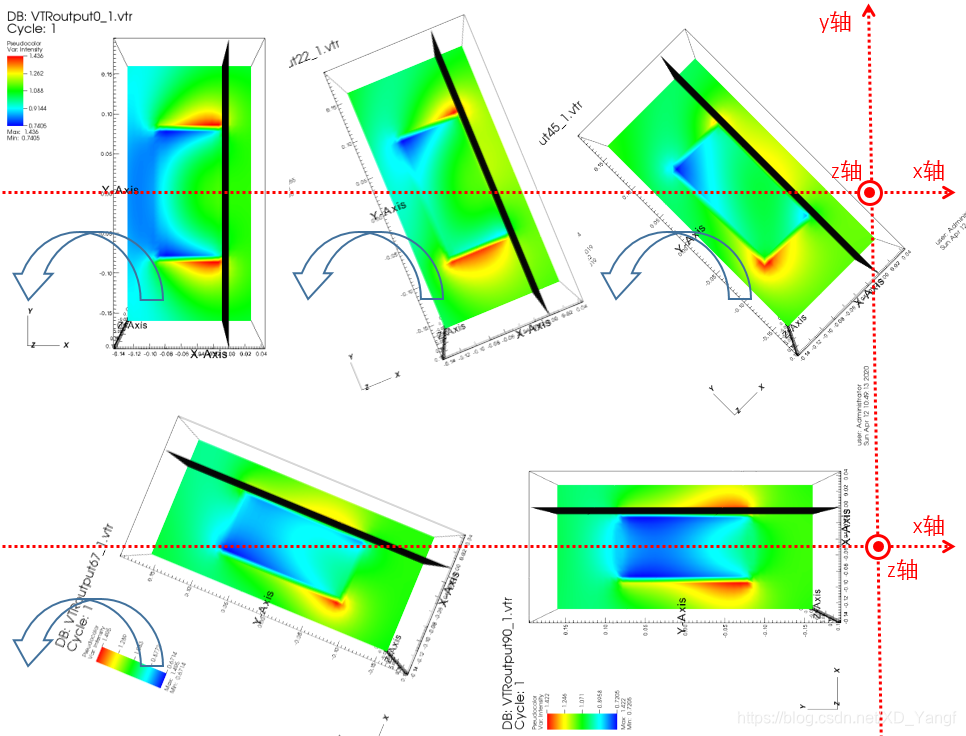
按照我们设定的THETA角度之后,手动在Vislt(本篇所有的可视化我都用了三维切面呈现)中转动模型之后,我们可以看到,此时的电场强度基本是以x、z平面上下对称的。这也就表明了,我画的这个坐标系是实际上的LF坐标系,且此时的入射光是沿我画出的x轴传播的(在这里,我们忽略Vislt图中左下角那个坐标系,不要管这个坐标方向)。
二、调整PHI角
1)PHI = 0, 22.5, 45, 67.5, 90 degree THETA = 0, BETA = 0
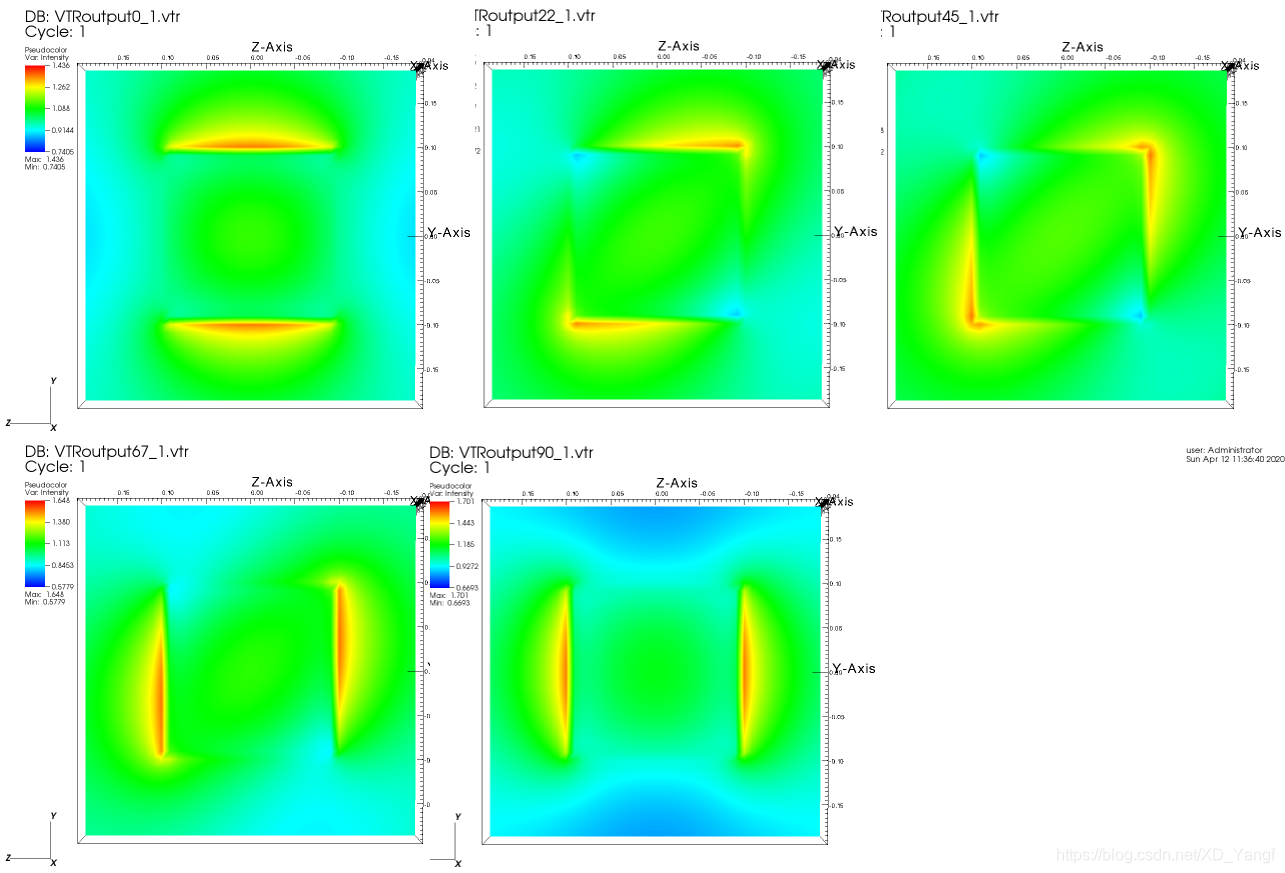
2) 调整角度之后看
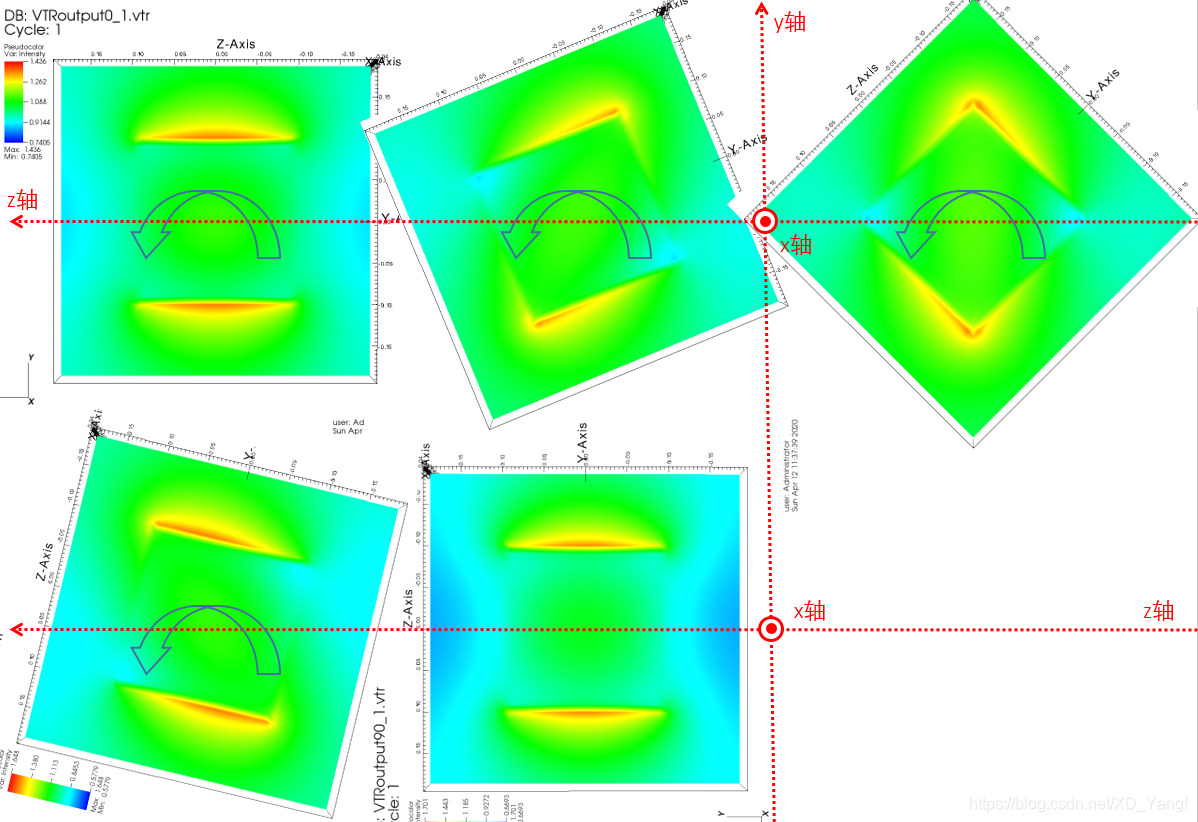
三、调整BETA角
1)BETA = 0, 22.5, 45, 67.5, 90 degree THETA = 0, PHI = 0

2) 调整角度之后看

没错,和调整PHI角时的结果一模一样。这不奇怪,因为,当THETA = 0 时,调整PHI和BETA的结果都是绕着x轴旋转。
因此,如果要显现PHI和BETA的区别,需要给THETA设定一个不为零的值。如下面四和五中的例子:
四、BETA和PHI的比较
1)THETA = 45 degree时,调整BETA角:BETA = 0, 22.5, 45, 67.5, 90 degree PHI = 0
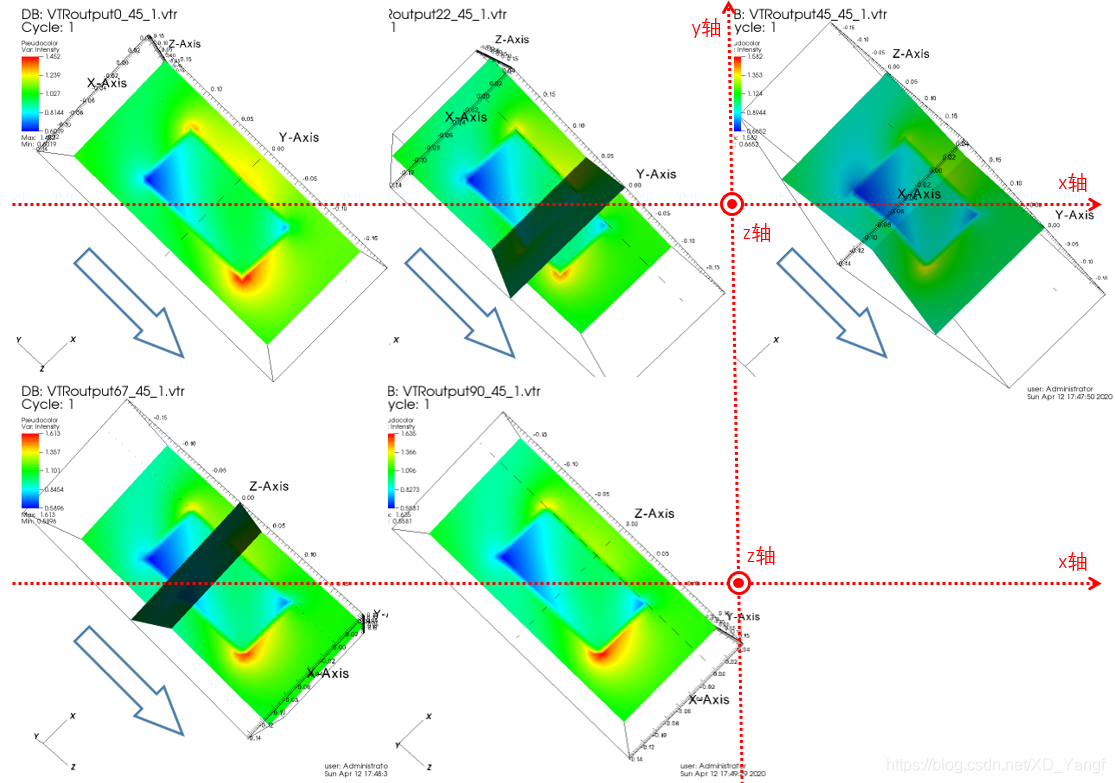
途中,蓝色边框箭头表示的是,目标的转动方向。可以看到上图中目标是围绕着我们看不见的a^1旋转,而下图中,是围绕着x轴旋转。
2)THETA = 45 degree时,调整PHI角:PHI = 0, 22.5, 45, 67.5, 90 degree BETA = 0
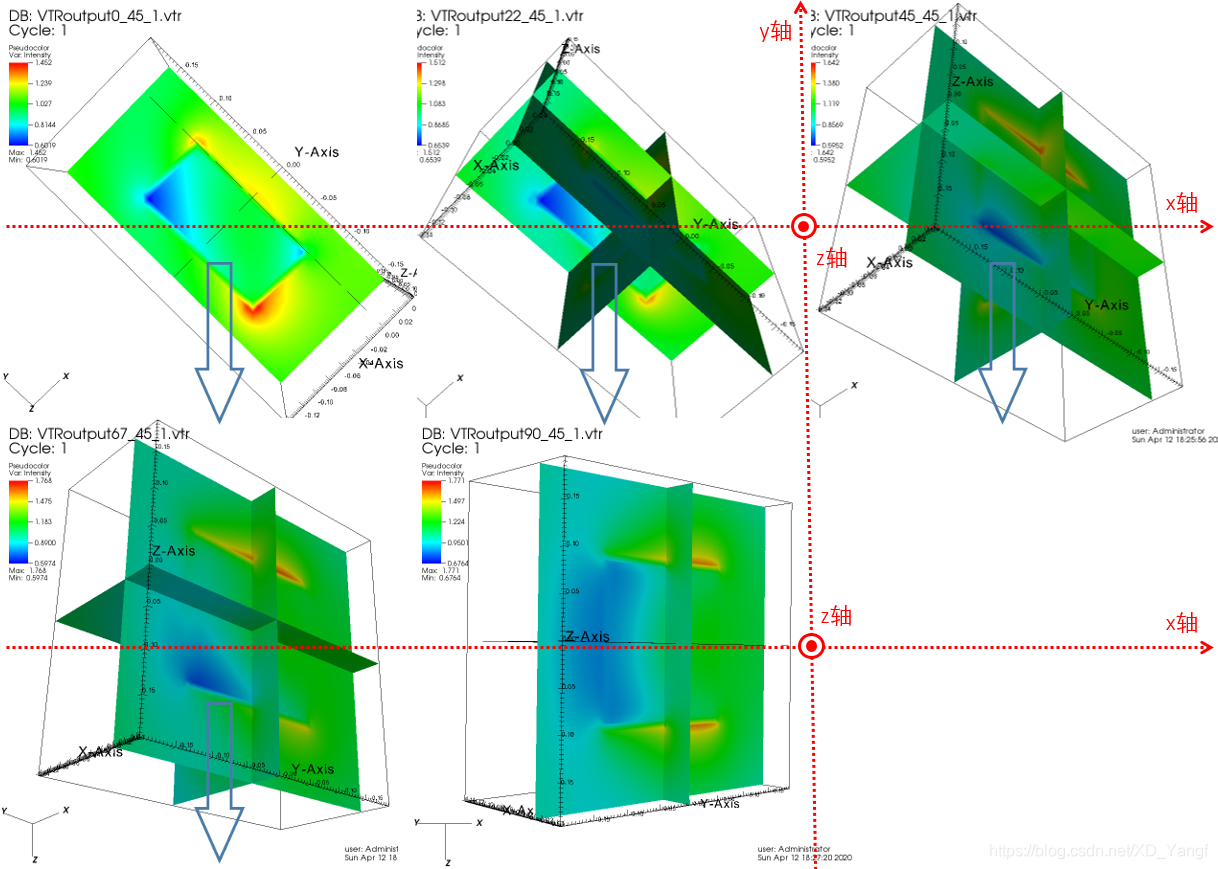
五、其他
对于角度的设定,比较麻烦,我们还需要考虑奇偶、首尾值、区间中值这些因素。而有一个简单的办法可以避开这些思考过程,就是我们每次选择只计算一个角度的模型(如果你不是大量研究角度变化的话),即:
'**** Prescribe Target Rotations ****'
0. 0. 1 = BETAMI, BETAMX, NBETA (beta=rotation around a1)
22.5 22.5 1 = THETMI, THETMX, NTHETA (theta=angle between a1 and k)
0. 0. 1 = PHIMIN, PHIMAX, NPHI (phi=rotation angle of a1 around k)
像这样设定就可以了,表示THETA转动22.5°,而其他角度都是0。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号