【Static Program Analysis - Chapter 4】格理论(Lattice Theory)与程序分析
# 从一个例子说起,
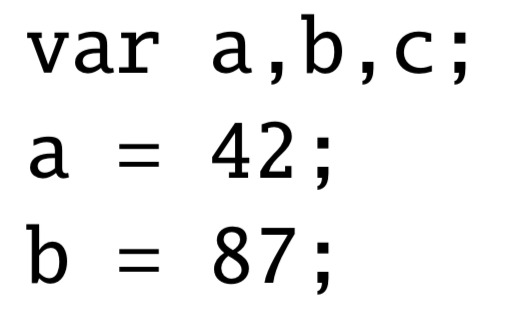
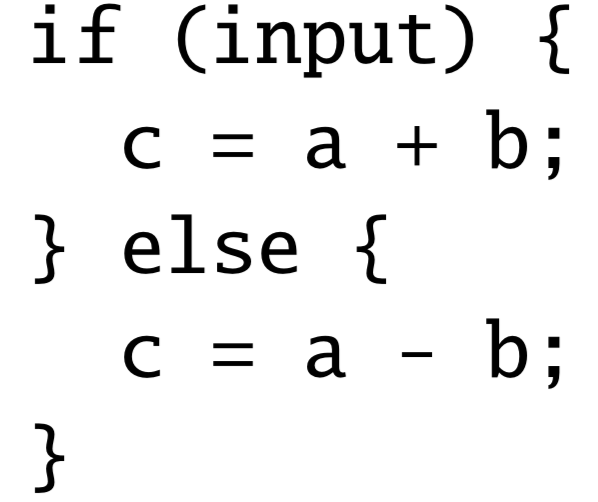
**任务:给定这样一段代码,假设我们想分析出这段代码中,每个数值型变量和表达式的符号,即正数,负数或0。**
此外,还有可能出现两种情况就是:
1.我们无法分析出结果,即我们无法确定符号,用(?)表示;
2.有些表达式的值并不是一个数字(例如,有可能是个指针)或者在执行的过程中没有被赋值(有可能是因为对于给定的输入,没有执行到,unreachable),用(⊥)表示。
因此,对于每一个变量或者是表达式,我们会有5种结果(这里将其表征成“格”的形式):
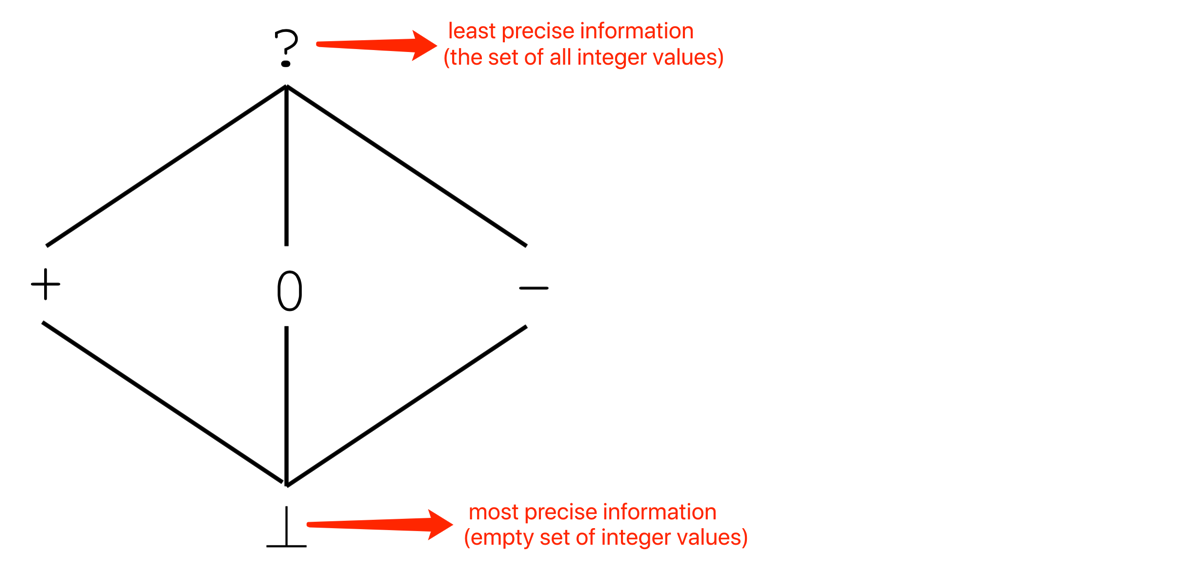
(?)可能的原因是:
1.执行多次,变量c是正数或者是负数的结果都出现过。所以标记为(?)更加保险;
2.分析方法无法证明结果的确定性。如,执行多次变量都是正数,但是分析方法无法证明变量一定是正数。
# 格理论(Lattice Theory)
## 偏序集合(Partially ordered set,简写poset)
首先了解一个概念叫*偏序集合*,(英语:Partially ordered set,简写poset)是数学中,特别是序理论中,指配备了部分排序关系的集合。 这个理论将排序、顺序或排列这个集合的元素的直觉概念抽象化。这种排序不必然需要是全部的,就是说不必要保证此集合内的所有对象的相互可比较性。部分排序集合定义了部分排拓扑。(更多详细的介绍见维基百科)
偏序:集合内只有部分元素之间在这个关系下是可以比较的。
比如:比如复数集中并不是所有的数都可以比较大小,那么“大小”就是复数集的一个偏序关系。
全序:集合内任何一对元素在在这个关系下都是相互可比较的。
比如:有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。
偏序关系即给定集合S,“≤”是S上的二元关系,若“≤”满足:
则称“≤”是S上的非严格偏序或自反偏序。
全序关系即集合X上的反对称的、传递的和完全的二元关系(一般称其为≤)。
若X满足全序关系,则下列陈述对于X中的所有a, b和c成立:
- 反对称性:若a ≤ b且b ≤ a则a = b
- 传递性:若a ≤ b且b ≤ c则a ≤ c
- 完全性:a ≤ b或b ≤ a
注意:完全性(全序)本身也包括了自反性。
所以,全序关系必是偏序关系。
## 格,a lattice is a pair(S,⊑)
在数学中,格是其非空有限子集都有一个上确界(叫并)和一个下确界(叫交)的偏序集合(poset)。格也可以特征化为满足特定公理恒等式的代数结构。因为两个定义是等价的,格理论从序理论和泛代数二者提取内容。半格包括了格,依次包括海廷代数和布尔代数。这些"格样式"的结构都允许序理论和抽象代数的描述。(更多详细的介绍见维基百科)
序理论定义
考虑任意一个偏序集合(L,≤),如果对集合L中的任意元素a,b,使得a,b在L中存在一个最大下界,和最小上界,则(L,≤)是一个格。
这里对于取a,b的最大下界的操作用
对于取a,b的最小上界操作用 
有界格有一个最大元素和一个最小元素,按惯例分别指示为1和0(也叫做顶和底)。任何格都可以通过增加一个最大元素和最小元素而转换成有界格。
使用容易的归纳论证,你可以演绎出任何格的所有非空有限子集的上确界(并)和下确界(交)的存在。一个很重要的格的种类是完全格。一个格是完全的,如果它的所有子集都有一个交和一个并,这对比于上述格的定义,这里只要求所有非空有限子集的交和并的存在。

例子:
任何一个有限的偏序集合可以表示成一张哈斯图(Hasse diagram,每个元素代表一个节点,顺序关系是边的传递闭包,由低到高),如,

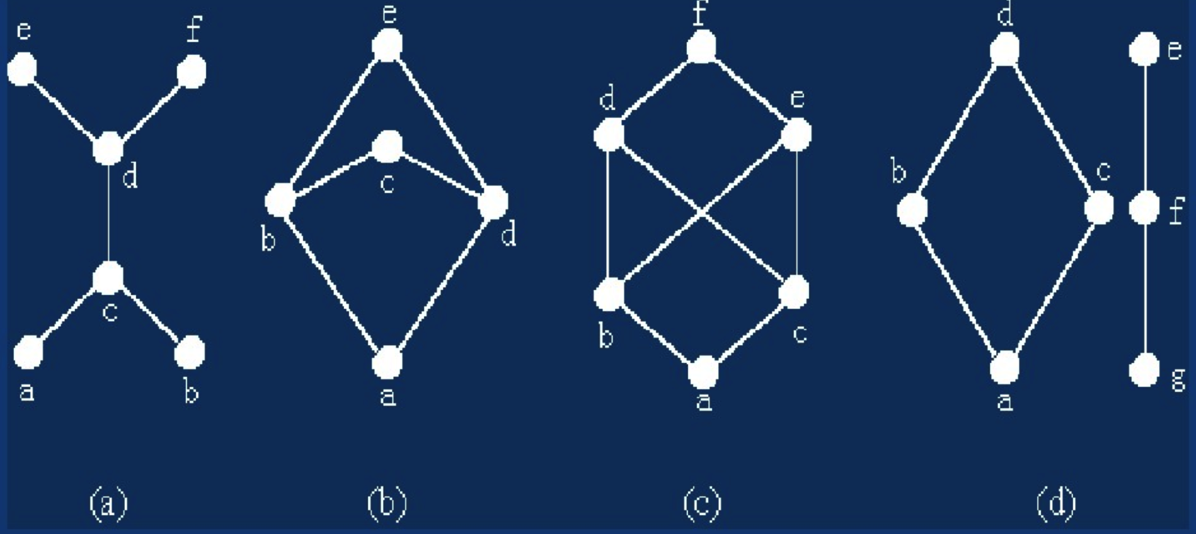
以上都是格,以下都不是格:
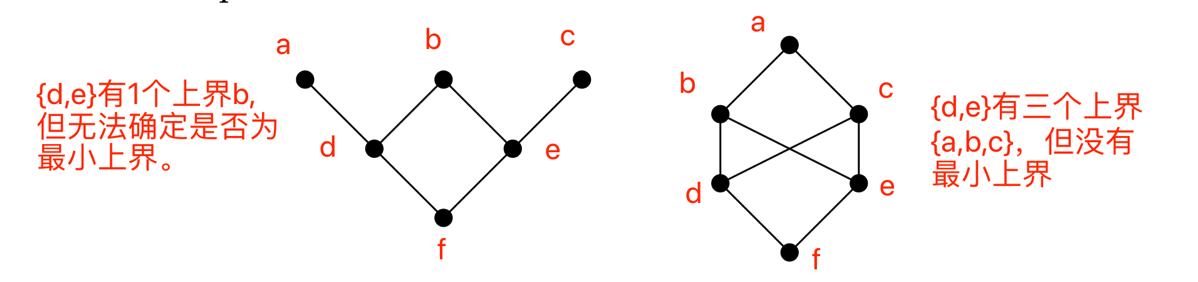
其他一些例子:

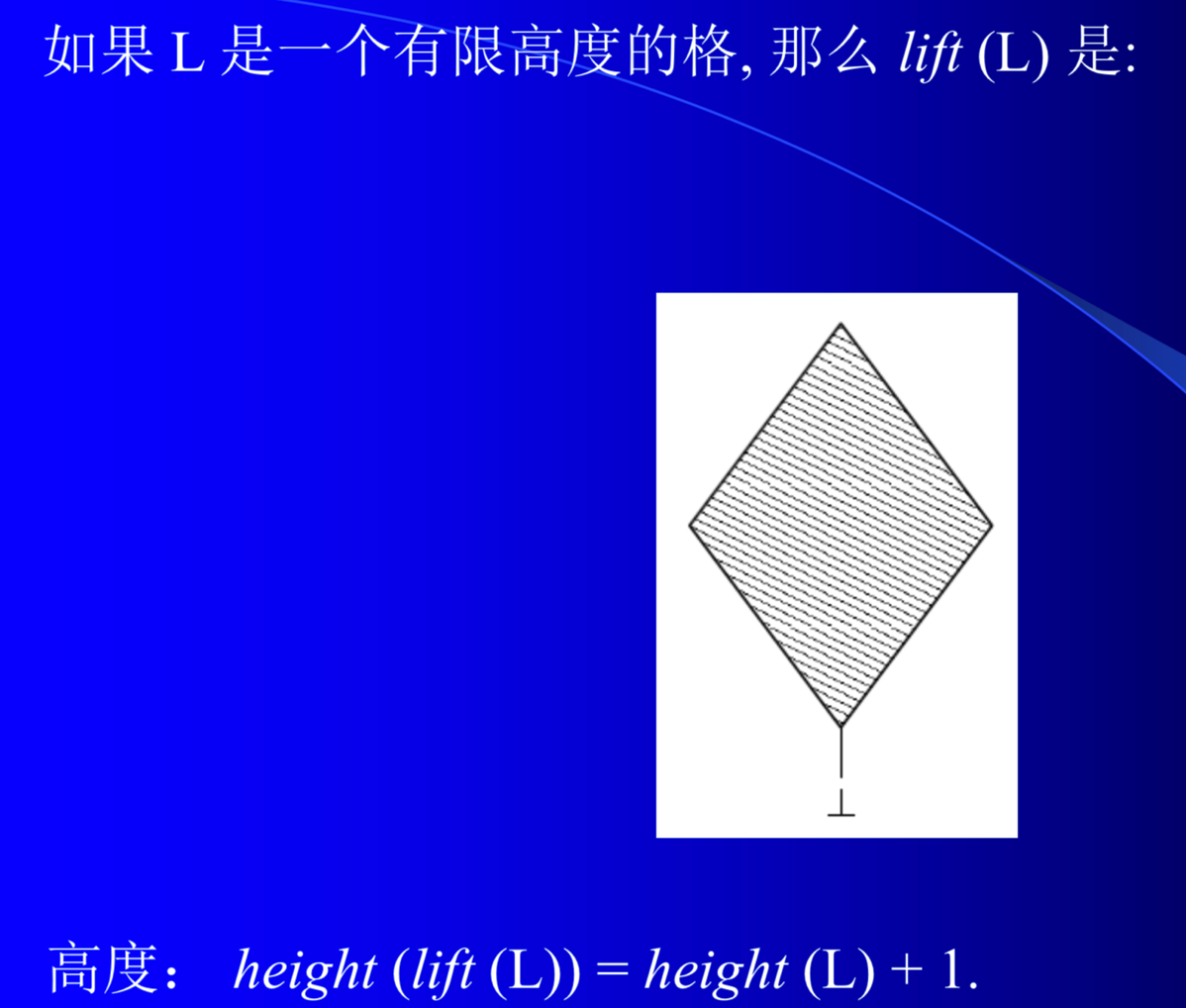
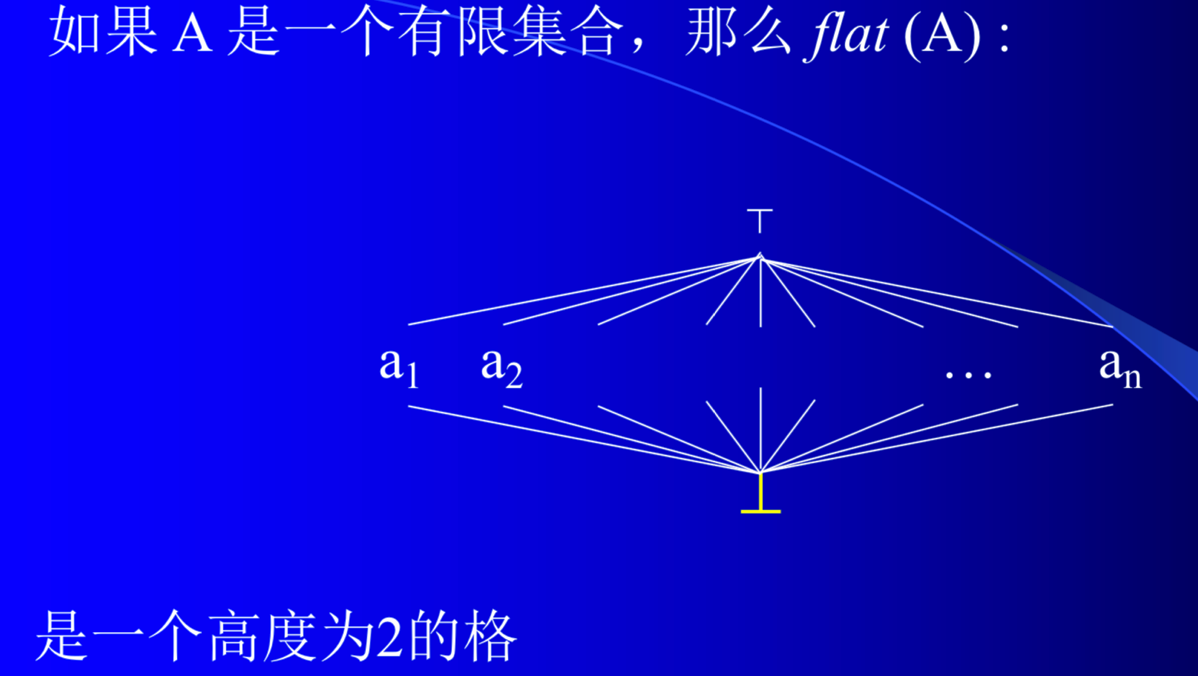
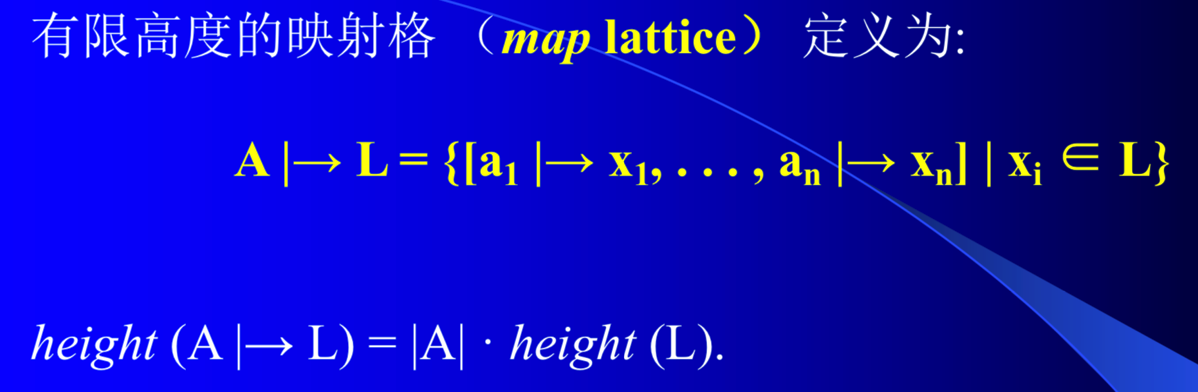
## 不动点(fixed-points)

这里引用王千祥老师的slide作为补充:







If you have any questions about this article, welcome to leave a message on the message board.
Brad(Bowen) Xu
E-Mail : maxxbw1992@gmail.com


 浙公网安备 33010602011771号
浙公网安备 33010602011771号