【cs229-Lecture4】GLMS:选定指数分布族,如何用它来推导出GLM?
在Lecture4中有3部分内容:
- Newton’s method 牛顿方法
- Exceponential Family 指数分布族
- Generalized Linear Models 广义线性模型(GLMS)
牛顿法上一篇随便中已经讲过了,是平行于梯度下降算法的另一种最优化算法。
然后,视频中证明了伯努利分布和高斯分布都属是指数分布族中的特例的证明,实际上就是把这两种分布转化为指数分布族的形式,然后一一去对照,判断是否符合。
接下来,就讲到了当我们选定了一个指数分布族之后,如何用它来推导出一个广义线性模型(GLM),也就是本文想要讲述的内容。
首先,给出三个假设,同时我们以伯努利分布为例(01问题建模)来进行说明:
给定一个指数分布族,之前我们已经证明了伯努利分布是指数分布族的特例,因此,它满足第一个假设。
给定X,目标是求出以X为条件的T(y)的期望E[T(y)|x],即让学习算法输出h(x)=E[T(y)|x],在此处,这个期望值就等于因变量取1的概率,一般就写成P了。这个P涵盖了0-1因变量的信息,同时也能够用来比较直观地理解我们的问题:当自变量发生变化时,我们的目标变量取1的概率是怎样变化的。
假设因变量取1的概率跟自变量是线性关系。
之后会补充例子。
If you have any questions about this article, welcome to leave a message on the message board.
Brad(Bowen) Xu
E-Mail : maxxbw1992@gmail.com


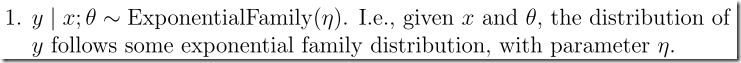




 浙公网安备 33010602011771号
浙公网安备 33010602011771号