数据结构导论十 图的存储结构

图的存储结构

1.邻接矩阵

图的邻接矩阵：表示图的个顶点之间的关系矩阵

 定义:G=（V,E）是n个顶点的图，则G的邻接矩阵为n阶方阵：

A[I][j]= 1时，若（vi,vj）或<vi,vj>属于E(G)

　　　 0时，则不属于

 

 

 

 

 

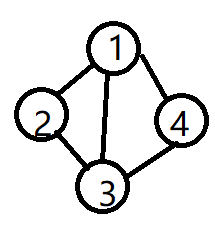
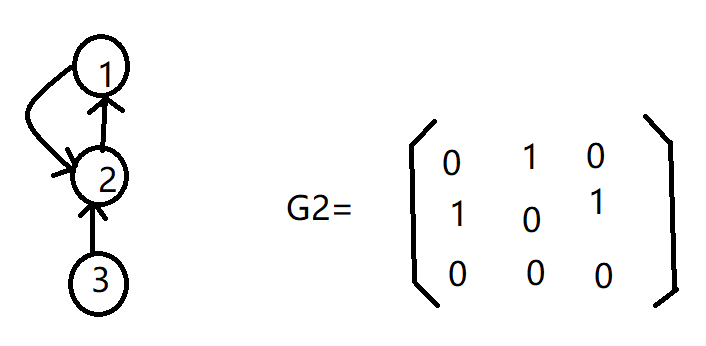
 无向图的邻接矩阵是对称的；

从邻接矩阵容易判断热议两顶点间是否有边相关联；

 

邻接矩阵的类型定义

const int vnum=20;
typedef struct gp
{ VertexType vexs[vnum]; //顶点信息
WeightType arcs[vnum][vnum]; //邻接矩阵
int vexnum,arcnum; //顶点数，边数
}WGraph;

 建立无向带权邻接矩阵：

将矩阵A的每个元素都初始化为最大值。

然后读入边和权值（i，j,wij)，将A的相应元素设为wij，

Void CreatGraph(Graph *g)
{ int i,j,n,e,w;
char ch;
scanf(“%d %d”,&n,&e);
g->vexnum=n;
g->arcnum=e;
for (i=0;i<g->vexnum;i++)
{
scanf(“%c”,&ch);
g->vexs[i]=ch;
}
for (i=0;i<g->vexnum;i++)
for (j=0;j<g->vexnum;j++)
g->arcs[i][j]=MAX_INT;、
for (k=0;k<g->arcnum;k++)
{
scanf(“%d %d %d”,&i, &j,&w);
g->arcs[i][j]=w;
g->arcs[j][i]=w;
}
}

1） n个顶点、 e条边的无向图，则其邻接表的表头结点数为n，
链表结点总数为2e；
2）对于无向图，第i个链表的结点数为顶点Vi的度；
对于有向图，第i个链表的结点数为顶点Vi的出度；
3）在边稀疏时，邻接表比邻接矩阵省单元；
4）邻接表表示在检测边数方面比邻接矩阵表示效率要高

邻接表的类型定义

#define vnum 20
Typedef struct arcnode
{ int adjvex; //下一条边的顶点编号
WeightType weight; //带权图的权值域
struct arcnode *nextarc； //指向下一条边的指针
}ArcNode;
Typedef struct vexnode
{ int vertex; //顶点编号
ArcNode *firstarc; //指向第一条边的指针
}AdjList[vnum];
Typedef struct gp
{ AdjList adjlist;
int vexnum,arcnum; //顶点和边的个数
}Graph;

　　图的遍历：

遍历含义以及方法：

图的遍历：从图G中某一顶点V出发，顺序访问个顶点一次

方法：

为克服顶点的重复访问，设立辅助数组visited[n]。
遍历方法：深度优先搜索DFC、广度优先搜索BFC

深度优先搜索法算法： 对图按深度优先遍历的递归算法（邻接表） ：
int visited[N]=0 ; /*对访问标记visited数组初始化*/
void Dfs ( Graph g , int v ) {
//从第v个顶点出发递归地深度优先遍历图g， 图以邻接表作为存储结构
ArcNode *p ;
printf ( “%d”,v ) ;
/* 访问起始顶点v*/
visited [v] = 1; /* 置“已访问” 标记*/
p = g.adjlist[v].firstarc ; /* 取顶点表中v的边表头指针*/
while ( p != NULL ) /* 依次搜索v的邻接点*/
{ if ( ! visited[p->adjvex] ) /*v的一个邻接点未被访问*/
Dfs ( g,p->adjvex ) ; /*沿此邻接点出发继续DFS*/
p = p->nextarc ; /* 取v的下一个邻接点*/
}
}

　　

深度优先搜索法算法： 对图按深度优先遍历的递归算法（邻接矩阵） ：
int visited[N]=0 ; /*对访问标记visited数组初始化*/
void Dfs ( Graph g , int v ) {
//从第v个顶点出发递归地深度优先遍历图g， 图以邻接矩阵作为存储结构
int j ;
printf ( “%d”,v ) ; /* 访问起始顶点v*/
visited [v] = 1; /* 置“已访问” 标记*/
for (j=0;j<n;j++) /* n为顶点数， j为顶点编号*/
{ m=g->arcs[v][j]; /*顺序访问矩阵的第v行结点*/
if （m&&!visited[j]） /*如果v与j邻接， 且j
未被访问*/
Dfs ( g,j ) ; /*递归访问j*/
}
}

　　

广度优先遍历算法：
int visited[N]=0 ; /*对访问标记visited数组初始化*/
int queue[N] ; /*队列queue存放已访问过的顶点*/
▲void 对图按广度优先遍历的算法： bfs (Graph g , int v ) {
// 从顶点v出发， 按广度优先遍历图g， 图用邻接表表示
printf(“%d”,v );
visited [v] = 1; /*访问初始顶点vi*/
rear=1; front=0;
queue[rear]=v ; /* 起始顶点（序号） 入队*/
while ( front!=rear ) /*队列不空， 则循环*/
{ front=(front+1)%N ; /*置队头*/
v=queue[front]; /* 队头元素出队*/
p=g.adjlist[v].firstarc; /*取刚出队顶点v的边表的头指针*/
while ( p!=NULL ) { /* 依次搜索v的邻接点*/
{ if (! visited[p->adjvex]) /*v的一个邻接点未被访问*/
{ printf (“%d”,p->adjvex) /*访问此邻接点*/
visited[p->adjvex] = 1 ;
rear=(rear+1)%N ; /*队尾指针增1*/
queue[rear]=p->adjvex; /*访问过的顶点入队*/
}
p=p->nextarc; } /* 找v的下一个邻接点*/
}
}/*bfs*/
Bfs (Graph g, int v)
{
LkQue Q; //Q为链队列
int j;
InitQueue(&Q);
printf(“%d”,v); //v为访问的起始结点
visited[v]=1; //访问过的标志
EnQueue(&Q,v);
while ( !EmptyQueue(Q)) //判队列是否为空
{ v=Gethead(&Q);
OutQueue(&Q); //出队列
for (j=0;j<n;j++) //n为顶点数，变化j依次尝试v的可能邻接点
{ m=g->arcs[v][j];
if (m && !visited[j]) //判断是否邻接点，且未被访问
{ printf(“%d”,j);
visited[j]=1; //置被访问标志
EnQueue(&Q,j); //邻接点入队列
}
}
}

　　

判断图的连通性
对图G调用一次DFS或BFS，得到一顶点集合，然后将
之与V(G)比较，若两集合相等，则图G是连通图，否则就
说明有未访问过的顶点，因此图不连通。

求图的连通分量
从无向图的每个连通分量的一个顶点出发遍历，
则可求得无向图的所有连通分量。
图遍历的一种应用
算法：
void trace( Graph G ) {
/*G为用邻接矩阵或邻接表表示的有n个顶点的无向图，求
该图的连通分量*/
int i;
for ( i=0; i<N; ++i )
if (!flag[i])
{ dfs(i);
/*调用DFS算法的次数仅决定于连通分量个数*/
OUTPUT ； /*输出访问到的顶点和依附于这*/
/*些顶点的边，就得到一个连通分量*/
}
}

　　

图的应用

生成树
1、 生成树定义：连通图G=(V,E)，从任一顶点
遍历，则图中边分成两部分：
遍历通过的边 剩下的边
(即遍历时未通过的边）
E(G) = T(G)+ B(G)
则G’(V， T)为G的子图，称之为G的一棵生成树。
●深度优先生成树： 按深度优先遍历而得的生成树
●广度优先生成树： 按广度优先遍历而得的生成树