数据结构导论 五 栈、队列和数组
栈
栈的定义:只是在表的一端进行插入和删除的线性表
其中:允许插入及删除一端(表尾)称为栈顶(top)
另一端(表头)称为栈底(Bottom)
当表中没有元素时称为空栈
S={i1,i2,i3,i4,i5,i6} 此时 i1称为栈底 i6称为栈顶

图1
进栈:在栈顶插入一个元素
出栈:在栈顶删除一个元素
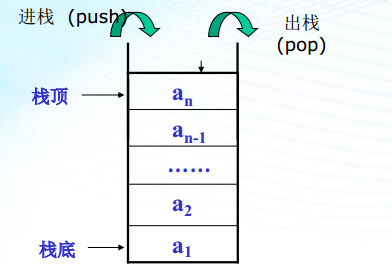
图2
特点:
通过图2 可以看出栈中的元素都是依次进入栈里面,第一个进入到栈里的称为栈底,越往上越是栈顶,而出栈的第一个元素则是栈顶。栈是先进后出的原则,栈称为“后进先出线性表LIFO”
栈的基本运算有哪些???
1)初始化栈:InitStack(S);
2)判断栈:EmptyStack(s);
3)进栈:push (S,x);
4)出栈:pop(s);
5)取栈:Gettop(s);
顺序栈以及常用名词
栈容量:栈中可以存放的最大元素个数
栈顶指针top:指示在当前栈顶元素在栈中位置
栈空:栈中无元素时,表示栈空
栈满:数组空间已被站满,成栈满
下溢:当栈空时,再要求出栈运算,称为“下溢”
上溢:当栈满时,再要求进栈运算,称为“上溢”
栈的运算:
初始化:
1 int Inistack(Seqstk *stk){ 2 3 stk->top=0; 4 5 return 1; 6 7 }
判断栈:
1 int EmptyStack(SeqStk *stk){ 2 3 if(stl->top==0)retrun 1; 4 5 esle reutn 0;}
进栈:
int push(seqstk *stk ,DataType x) if(stk->top == masize-1)//判断是否上溢 {error("栈满");return 0;//上溢 } else{ stk->top++;//修改栈顶指针, stk->data[sq->top]=x//元素x插入新栈顶中 return 1; }
出栈:
int pop(seqstk *stk){ if(stk->top==0)//判断是否需要下溢 {error("栈空");return 0;}//下溢 else{ stk->toop;return 1;}//修改栈顶指针,指向新栈顶 }
取栈顶元素
1 DataType GetTop(SeqStk *stk) 2 { 3 if(EmptyStack(stk)) 4 return NULLData; 5 else 6 return stk->data[stk->top]; 7 }
链栈的定义
栈的链式存储结构称为链栈,他是运算受限的的单链表,插入和删除操作今现制在表头位置上进行。栈顶指针就是链表的头指针。

链栈的如何运算呢???
初始化:
1 void InitStack(Lkstk *Ls){ 2 Ls=(LKstk*)malloc(sizeof(Lkstk)); 3 Ls->next=null; 4 }
判断栈
1 nt EmptyStack(LkStk *LS) 2 { 3 if(LS->next= =NULL) return 1; 4 else return 0; 5 }
进栈
void Push (LkStk *LS, DataType x) { LkStk *temp; temp= (LkStk *) malloc (sizeof (LkStk)); temp->data=x; temp->next=LS->next; LS->next=temp; }
出栈
1 int Pop (LkStk *LS) 2 { LkStk *temp; 3 if (!EmptyStack (LS)) 4 { temp=LS->next; 5 LS->next=temp->next; 6 free(temp); 7 return 1; 8 } 9 else return 0; 10 }
取栈顶元素
DataType GetTop(LkStk *LS) { if (!EmptyStack(LS)) return LS->next->data; else return NULLData; }
队列
队列也是一种运算受限的的线性表
队列:是只允许在表的一端进行插入,而在另一端进行阐述的线性表
如果将栈比作一个口开的公交车(先下后上),那么队列就可以比作两口开的公交(前门进后门出)
对头:允许删除一端称为对头(front)
队尾:允许插入的另一端称为队尾(rear)
队列:Q={a1,a2,a3,a4,a5,a5。。。}
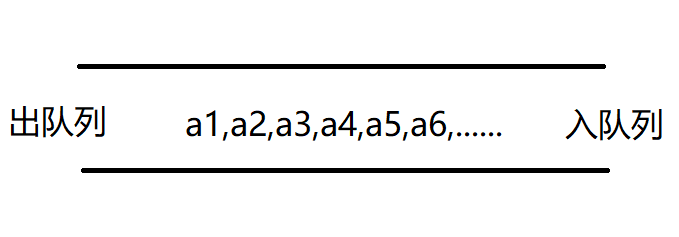
队列:先进先出FIFO
队列的基本运算都有那些???
- 队列初始化 InitQueue(Q):
- 设置一个空队列Q;
- 判队列空 EmptyQueue(Q):
- 若队列Q为空,则返回值为1,否则返回值为0;
- 入队列 EnQueue(Q,x):
- 将数据元素x从队尾一端插入队列,使其成为队列的新尾元素;
- 出队列 OutQueue(Q):
- 删除队列首元素;
- 取队列首元素GetHead(Q):
- 返回队列首元素的值。

初始化:front=rear=0
进队:rear加1,元素插入尾指针位置
出队:front加1,去头指针所值位置
顺序队列:
上溢条件:sq.rear==maxsize-1(队满)
下溢条件:sq.rear==sq.front(队列空)
循环队列
定义:为队列分配一块存储空间,并将这块存储空间看成头尾相连接的。
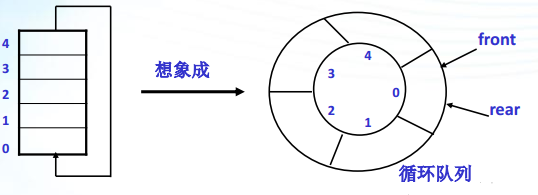
循环队列的实现
对插入即入队列:队尾指针增1
sq.rea(sq.rear+1)1%maxsize
对删除即出队:对头指针增1
sq.front=(sq.front+1)%maxsize
循环队列规定:
下溢条件即队列空:CQ.front==CQ.rear
上溢条件即队列满:尾指针从后面追上头指针
(CQ.rear+1)%maxsize==cq.front(尾赶头)
循环队列的基本运算:
队列初始化
1 void InitQueue(CycQue CQ){ 2 CQ.front=0;CQ.rear=0;}
判断队列
1 int EmptyQueue(CycQue CQ) 2 {if (CQ.rear==CQ.front) return 1; 3 else return 0;}
入队列
int EnQueue(CycQue CQ,DataType x) {if ((CQ.rear+1)%maxsize==CQ.front) {error(“队列满” );return 0;} else {CQ.rear=(CQ.rear+1)%maxsize; CQ.data[CQ.rear]=x; return 1;} }
出队列
int OutQueue(CycQue CQ) {if (EmptyQueue(CQ)) {error(“队列空” ); return 0; } else {CQ.front=(CQ.front+1)%maxsize; return 1; } }
取队列首元素
DataType GetHead(CycQue CQ) { if (EmptyQueue(CQ)) return NULLData; else return CQ.data[(CQ.front+1)%maxsize]; }
链队列的基本运算
队列的初始化
1 void init Queue(LkQue *LQ){ 2 LkQueNode *temp; 3 temp=(LkQuenode*)malloc(sizeof(LkQueNode)); 4 LQ->front=temp; 5 LQ->rear=temp; 6 (LQ->front)->next=NULL; 7 }
判队列空
1 Int EmptyQueue(LKQue LQ){ 2 if(LQ.rear==LQ.front)return 1; 3 else return 0; 4 }
入队列:

1 Void EnQueue(LkQue *LQ;DataType x) 2 { 3 LkQueNode *temp; 4 temp=(LkQueNode *)malloc(sizeof(LkQueNode)); 5 temp->data=x; 6 temp->next=NULL; 7 (LQ->rear)->next=temp; 8 LQ->rear=temp; 9 }
出队列:
1 OutQueue(LkQue *LQ) 2 { LkQueNode *temp; 3 if (EmptyQueue(LQ)) 4 {error(“队空” ); return 0; } 5 else { 6 temp=(LQ->front)->next; 7 (LQ->front)->next=temp->next; 8 if (temp->next==NULL) LQ->rear=LQ->front; 9 free(temp); 10 return 1; 11 } 12 }
取队列首元素
1 DataType GetHead (LkQue LQ) 2 { 3 LkQueNode *temp; 4 if (EmptyQueue(LQ)) 5 return NULLData; 6 else { 7 temp=LQ.front->next; 8 return temp->data; 9 } 10 }
数组
数组可以看成一种特殊的线性表,其特殊在于,表中的数组元素本身也是一种线性表。
数据的逻辑结构与运算
数组是线性表的推广,其每个元素由一个值和一组下标组成,其中下标数称为数组的维数。
二维数组Amn可以看成是m个行向量组成的向量,也可以看成是n个列向量组成的向量
数组一旦被定义,它的维数和维界就不再改变。因此,除了结构的初始化和销毁之外,数组通常只有两种基本运算:
读:给定一组下标,读取相应的数据元素;
写:给定一组下标,修改相应的数据元素;
寻址公式:
例如, 二维数组Amn按“行优先顺序”存储在内存中,假设每个元素占用k个存储单元。
元素aij的存储地址应是数组的基地址加上排在aij前面的元素所占用的单元数。因为aij位于第i行、第j列,前面i行一共有i×n个元素,第i行上aij前面又有j个元素,故它前面一共有i×n+j个元素,
因此, aij的地址计算函数为:LOC(aij)=LOC(a00)+(i*n+j)*k
矩阵的压缩存储
为了节省存储空间,我们可以对这类矩阵进行压缩存储:即为多个相同的非零元素值分配一个存储空间;对零元素不分配空间。
1.对称矩阵:
定义:在一个n阶方阵A中,若元素满足下述性质:aij=aji , 0<=i,j<n-1
则成A为对称矩阵。
物理存储:
对称矩阵中元素关于主对角线对称,故只要存储矩阵中上三角或下三角中的元素,让每两个对称的元素共享一个存储空间。
它的公式:i=n(n+1)/2
下标变换公式
1)若i>=j,则下三角形中,a[ij]之前的i行(从第0行道第i-1行)一共由1+2+。。。=i(i+1)/2个元素,在第i行上,a[ij]之前由j个元素,
因此有:k=i*(i+1)/2+j 0<=k<n(n+1)/2-1
2)若i<j,则a[ij]是在上三角矩阵中,因为aij=aji,所以只要交换上述对应关系中的i和j即可得到
k=j*(j+1)/2+i 0<=k<n(n+1)/2-1
令 I=max(i,j), J=min(i,j),则k和 i, j的对应关系
可统一为: k=I*(I-1)/2+J 0≤k<n(n+1)/2 -1
三角矩阵:
三角矩阵中的重复元素C可共享一个存储空间,其余的元素正好有n(n+1)/2个,因此,三角矩阵可以压缩存储道向量s[0...n(n+1)/2]中,其中c存放在向量的最后一个分量中
上三角:
当i<=j时 k=i( 2n-1+1)/2+j-i
当i>j时 k=n(n+1)/2
下三角:
当i>=j时: k=i(i+1)/2+j
当i<j时: k=j(j+1)/2+i



 浙公网安备 33010602011771号
浙公网安备 33010602011771号