DirectX11 With Windows SDK--04 变换

回到顶部

前言

这一章涉及的是常用的矩阵变换，绝大部分内容节选自龙书，以帮助大家构建矩阵与2D/3D空间的数学联系。

学习目标：

了解Direct3D的一些内在规定
掌握矩阵变换与2D/3D空间的联系
熟悉3D变换与投影成像的过程
熟悉2D变换与投影成像的过程

DirectX11 With Windows SDK完整目录

Github项目源码

欢迎加入QQ群: 727623616 可以一起探讨DX11，以及有什么问题也可以在这里汇报。

回到顶部

Direct3D的一些规定

3D坐标系

Direct3D使用的是左手坐标系，而OpenGL与我们平日接触到的数学使用的则是右手坐标系：

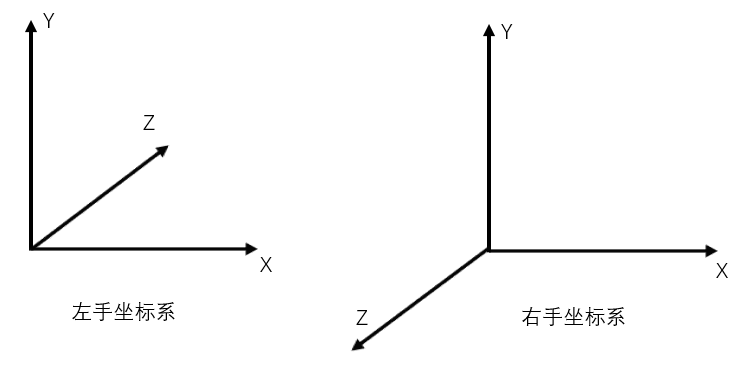
我们可以用左手摆出上图中的左手坐标系，其中拇指朝向+X，食指朝向+Y，中指朝向+Z

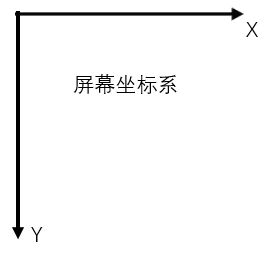
纹理坐标系和屏幕坐标系

为了避免混淆，这里直说Direct3D的。由于Direct3D支持3D纹理，纹理坐标系实际上是可以有三个维度的，如下图所示。只不过我们绝大多数情况使用的仅仅是2D纹理，故只需要考虑X轴和Y轴的部分。

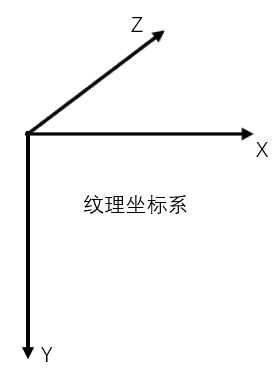
屏幕坐标系（2D）与纹理坐标系的X轴、Y轴朝向是一致的。

矩阵计算

Direct3D中，矩阵通常被表示为行矩阵，即你将要使用到的DirectXMath数学库中生成的矩阵都是行矩阵。这也意味着矩阵乘法通常被表示为行向量乘以行矩阵的形式。这不仅在编写C++的代码中有所体现，在HLSL中我们也将习惯写成上述形式。

回到顶部

矩阵变换

基、基向量

由于上面我们提到DirectX使用的是行矩阵，因此我们的基向量也为行向量。基向量是构成坐标系的包含大小的坐标轴，而3D坐标系的基是由3个基向量组成的。而3个模为1，且相互正交的基向量构成的基叫做标准正交基，其中(1,0,0), (0,1,0)和(0,0,1)则作为标准正交基的3个标准基向量

变换矩阵

变换矩阵是通过与顶点坐标(或向量)进行矩阵乘法来实现对顶点的变换，变换得到的顶点坐标（或向量）为在原坐标系下对应的坐标。

例如有下图的这样一个变换，y轴缩小为原来的1/2，而z轴加上1个单位的x轴向量得到新的z轴。

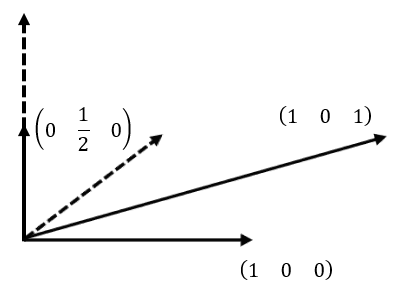
现有一坐标(2,4,1)，上述变换过程可以用下面的矩阵乘法表示：

[\begin{matrix} 2 & 4 & 1 \end{matrix}] [\begin{matrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 1 & 0 & 1 \end{matrix}] = [\begin{matrix} 3 & 2 & 1 \end{matrix}]

$\begin{bmatrix} 2 & 4 & 1\end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 1 & 0 & 1 \\ \end{bmatrix}=\begin{bmatrix} 3 & 2 & 1\end{bmatrix}$

其中3x3矩阵的3个行向量从上往下依次为变换后的坐标基的x'轴(或向量i')、y'轴(或向量j')和z'轴(或向量k')。这种变换的一般形式为：

[\begin{matrix} x & y & z \end{matrix}] [\begin{matrix} ⟵ \vec{i^{'}} ⟶ \\ ⟵ \vec{j^{'}} ⟶ \\ ⟵ \vec{k^{'}} ⟶ \end{matrix}] = [\begin{matrix} x^{'} & y^{'} & z^{'} \end{matrix}]

$\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix} \longleftarrow\vec{\mathbf{i'}}\longrightarrow \\ \longleftarrow\vec{\mathbf{j'}}\longrightarrow \\ \longleftarrow\vec{\mathbf{k'}}\longrightarrow \\ \end{bmatrix}=\begin{bmatrix} x' & y' & z'\end{bmatrix}$

线性变换

缩放

缩放（scaling）是指改变物体的大小。通过分别改变x轴、y轴、z轴的比例我们可以得到想要的物体大小，以及宽窄、高低、厚扁程度。

缩放矩阵的表示为：

S = [\begin{matrix} S_{x} & 0 & 0 \\ 0 & S_{y} & 0 \\ 0 & 0 & S_{z} \end{matrix}]

$S=\begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & S_z \\ \end{bmatrix}$

在DirectXMath中，缩放矩阵对应的函数为XMMatrixScale

旋转

旋转（rotation）是为了改变物体的朝向。在初学阶段我们常用的是绕x轴、y轴、z轴旋转的变换。需要注意的是，DirectXMath中的旋转变换都是顺时针旋转（theta > 0表示顺时针旋转）。

但现在暂时先让我们回到一般数学上（右手坐标系）。现在我们需要让向量或坐标点(x, y)绕原点逆时针旋转β度：

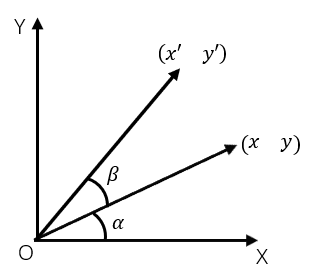
变换前的向量用极坐标表示为：

x = r c o s α y = r s i n α

$x=rcos\alpha \\ y=rsin\alpha$

逆时针旋转β度后的向量用极坐标表示为：

x^{'} = r c o s (α + β) = r c o s α c o s β - r s i n α s i n β = x c o s β - y s i n β y^{'} = r s i n (α + β) = r s i n α c o s β + r s i n β c o s α = x s i n β + y c o s β

$x'=rcos(\alpha + \beta) = rcos\alpha cos\beta - rsin\alpha sin\beta = xcos\beta - ysin\beta \\ y'=rsin(\alpha + \beta) = rsin\alpha cos\beta + rsin\beta cos\alpha = xsin\beta + ycos\beta$

上述变换过程我们可以用矩阵表示为：

[\begin{matrix} x & y \end{matrix}] [\begin{matrix} c o s β & s i n β \\ - s i n β & c o s β \end{matrix}] = [\begin{matrix} x^{'} & y^{'} \end{matrix}]

$\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} cos\beta & sin\beta \\ -sin\beta & cos\beta \\ \end{bmatrix}=\begin{bmatrix} x' & y' \end{bmatrix}$

这里省略3D空间下分别绕X,Y,Z轴逆时针旋转的矩阵推导过程，我们可以得到下面3个对应的矩阵：

R_{x} = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ & s i n θ \\ 0 & - s i n θ & c o s θ \end{matrix}], R_{y} = [\begin{matrix} c o s θ & 0 & - s i n θ \\ 0 & 1 & 0 \\ s i n θ & 0 & c o s θ \end{matrix}], R_{z} = [\begin{matrix} c o s θ & s i n θ & 0 \\ - s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}]

$\mathbf{R_x}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta & sin\theta \\ 0 & -sin\theta & cos\theta \\ \end{bmatrix}, \mathbf{R_y}=\begin{bmatrix} cos\theta & 0 & -sin\theta \\ 0 & 1 & 0 \\ sin\theta & 0 & cos\theta \\ \end{bmatrix}, \mathbf{R_z}=\begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

需要注意的是，因为左手坐标系跟右手坐标系是镜像关系，因此右手坐标系下的绕某一轴逆时针旋转（在轴的朝向处向原点看）所用的矩阵，和左手坐标系下的绕同一轴顺时针旋转（在轴的朝向处向原点看）所用的矩阵是相同的。

例如，在左手坐标系下，对向量[sqrt(2), sqrt(2), 1, 0]绕Z轴顺时针旋转45°（从Z轴正方向往原点看）的运算过程如下：

[\begin{matrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 1 & 0 \end{matrix}] [\begin{matrix} c o s 45 ° & s i n 45 ° & 0 & 0 \\ - s i n 45 ° & c o s 45 ° & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} 0 & 1 & 1 & 0 \end{matrix}]

$\begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 1 & 0 \end{bmatrix}\begin{bmatrix} cos45° & sin45° & 0 & 0 \\ -sin45° & cos45° & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}=\begin{bmatrix} 0 & 1 & 1 & 0 \end{bmatrix}$

此外，旋转矩阵具有正交性，即满足 $\mathbf{R^T} = \mathbf{R^{-1}}$ 。

在DirectXMath中，缩放矩阵对应的函数为XMMatrixRotationX、XMMatrixRotationY、XMMatrixRotationZ（参数为弧度）

注意：除了旋转和平移，只要三个基向量线性无关（即不共面），就都可以称之为线性变换。就如同变换矩阵那一小节所用到的矩阵那样。

仿射变换

齐次坐标

仿射变换是由一个线性变换与一个平移变换组合而成的。对于向量而言，平移操作是没有意义的，因为向量只描述方向与大小、却与位置无关，即平移操作不应作用于向量。因此，平移变换只能应用于点（位置向量）。齐次坐标（homogeneous coordinate）所提供的表示机制，使我们可以方便地对点和向量进行统一的处理。在采用其次坐标表示法时，我们将坐标扩充为四元组，第四个坐标w的取值将根据被描述对象是点还是向量而定：

(x, y, z, 0)表示向量
(x, y, z, 1)表示点

注意：这种表示法可以很方便地表示两个坐标点之差即为一个向量（w分量为0），以及表示一个点与一个向量之和为一个点（w分量为1）

(x, y, z, w)和(x/w, y/w, z/w, 1)都表示同一个点(w≠0)，这对于后续做透视投影会用到这个性质

仿射变换的定义及矩阵表示

线性变换并不能表示出我们需要的所有变换，因此，现将其扩充为一种称作仿射变换的映射范围更广的函数类。仿射变换的矩阵表示法为：

[\begin{matrix} x & y & z \end{matrix}] [\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}] + [\begin{matrix} t_{x} & t_{y} & t_{z} \end{matrix}] = [\begin{matrix} x^{'} & y^{'} & z^{'} \end{matrix}]

$\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}+\begin{bmatrix} t_x & t_y & t_z\end{bmatrix}=\begin{bmatrix} x' & y' & z'\end{bmatrix}$

如果用w = 1把坐标扩充为齐次坐标，那么就可以将上式更加简洁地写作：

[\begin{matrix} x & y & z & 1 \end{matrix}] [\begin{matrix} a_{11} & a_{12} & a_{13} & 0 \\ a_{21} & a_{22} & a_{23} & 0 \\ a_{31} & a_{32} & a_{33} & 0 \\ t_{x} & t_{y} & t_{z} & 1 \end{matrix}] = [\begin{matrix} x^{'} & y^{'} & z^{'} & 1 \end{matrix}]

$\begin{bmatrix} x & y & z & 1 \end{bmatrix}\begin{bmatrix} a_{11} & a_{12} & a_{13} & 0 \\ a_{21} & a_{22} & a_{23} & 0 \\ a_{31} & a_{32} & a_{33} & 0 \\ t_x & t_y & t_z & 1 \\ \end{bmatrix}=\begin{bmatrix} x' & y' & z' & 1 \end{bmatrix}$

若把w改成0，它就不会受到向量t平移的影响。

平移

现在将平移变换定义为仿射变换。若要利用向量t对坐标点u进行平移，则这种变换矩阵可以表示为：

T = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_{x} & t_{y} & t_{z} & 1 \end{matrix}]

$\mathbf{T}=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_x & t_y & t_z & 1 \\ \end{bmatrix}$

平移矩阵的逆矩阵表示平移的逆操作，即为利用向量-t对坐标点u进行平移：

T^{- 1} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - t_{x} & - t_{y} & - t_{z} & 1 \end{matrix}]

$\mathbf{T^{-1}}=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -t_x & -t_y & -t_z & 1 \\ \end{bmatrix}$

变换的复合

假设S是一个缩放矩阵，R是一个旋转矩阵，T是一个平移矩阵。对几何体的变换顺序通常为先缩放，后旋转，再平移。对几何体的每个顶点，都有：

((v_{i} S) R) T = {v_{i}}^{^{'}}

$((v_i S)R)T={v_i}^{'}$

因为矩阵乘法满足结合律，故可以先计算SRT，再计算vi与SRT的乘积。又或者将C=SRT看作一个矩阵，即提前将3种变换封装为一个净变换矩阵。对于一个包含20000顶点组成的3D物体，如果按照上式进行计算，则需要执行60000次的向量与矩阵的乘法运算；而预先将C算出来的话，则只需要执行2次矩阵乘法运算和20000次向量与矩阵的乘法运算。

但是，矩阵乘法并不满足交换律！这意味着诸如SR与RS，RT与TR的变换结果很可能是不同的。

下图展示了立方体先按X轴放大为原来的两倍，再绕Y轴顺时针旋转30°（图上半部分），以及先绕Y轴顺时针旋转30°，再按X轴放大为原来的两倍的结果（图下半部分）：

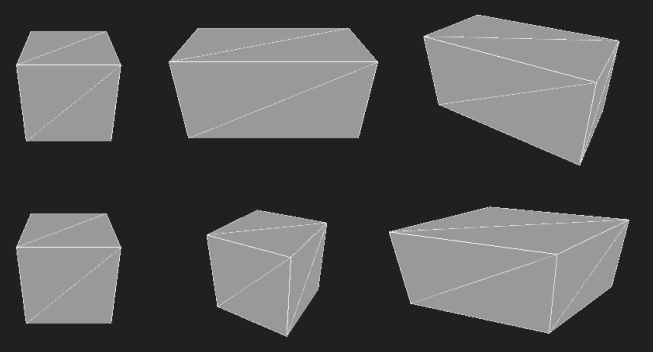
可以看到，先旋转后缩放会导致物体的畸变。

坐标变换

坐标变换的矩阵为：

[\begin{matrix} x & y & z & w \end{matrix}] [\begin{matrix} ⟵ \vec{u} ⟶ & 0 \\ ⟵ \vec{v} ⟶ & 0 \\ ⟵ \vec{w} ⟶ & 0 \\ ⟵ \vec{Q} ⟶ & 1 \end{matrix}] = [\begin{matrix} x & y & z & w \end{matrix}] [\begin{matrix} u_{x} & u_{y} & u_{z} & 0 \\ v_{x} & v_{y} & v_{z} & 0 \\ w_{x} & w_{y} & w_{z} & 0 \\ Q_{x} & Q_{y} & Q_{z} & 1 \end{matrix}] = [\begin{matrix} x^{'} & y^{'} & z^{'} & w \end{matrix}]

$\begin{bmatrix} x & y & z & w \end{bmatrix}\begin{bmatrix} \longleftarrow\vec{\mathbf{u}}\longrightarrow & 0 \\ \longleftarrow\vec{\mathbf{v}}\longrightarrow & 0 \\ \longleftarrow\vec{\mathbf{w}}\longrightarrow & 0 \\ \longleftarrow\vec{\mathbf{Q}}\longrightarrow & 1 \\ \end{bmatrix}= \begin{bmatrix} x & y & z & w \end{bmatrix}\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ w_x & w_y & w_z & 0 \\ Q_x & Q_y & Q_z & 1 \\ \end{bmatrix}= \begin{bmatrix} x' & y' & z' & w \end{bmatrix}$

坐标变换矩阵其实就是仿射变换矩阵的一种，即本质上坐标变换矩阵和仿射变换矩阵是相同的，但是在看待这种变换的过程会有所不同。在讲变换矩阵的时候，我们是让坐标系不变，然后让物体在当前坐标系下进行缩放、旋转和平移来到最终的位置；但在讲坐标变换的时候，我们是让整个坐标系缩放、旋转（带动物体的缩放和旋转），然后再让坐标系远离物体以完成所谓的平移操作。它们的差别仅仅在于选择的参考系不同而已。如果能理解这一点，对于接下来的世界变换、观察变换和投影变换理解都有所帮助。这样我们就能够清楚，既然坐标变换可以让坐标轴远离物体（以物体为参考系），那么坐标变换的逆变换可以让坐标轴靠近物体（以物体为参考系）。

回到顶部

3D的变换与投影成像

3D的部分包含了四大变换：世界变换、观察变换、投影变换和视口变换。其中前面三种变换需要在顶点着色器完成，必要时需要提供变换矩阵。而视口变换是在光栅化阶段完成的，通过第一章传给光栅化阶段的D3D11_VIEWPORT来完成。

局部空间与世界空间

每个物体都有其自己的局部空间（局部坐标系），但是世界空间只有一个。

世界变换囊括了缩放、旋转和平移变换。通过世界变换，我们可以将物体模型从自身的局部坐标系转换到世界坐标系中。当然，我们也可以理解为将物体从世界原点开始缩放、旋转，然后平移到目标位置。这样每一个物体都能在同一个世界空间中表示。

注意：对于不同的物体，需要使用不同的世界变换矩阵；而对于同一个物体的所有顶点，都要使用一致的世界变换矩阵来变换。

从局部空间到世界空间的坐标变换矩阵即为前面提到的：

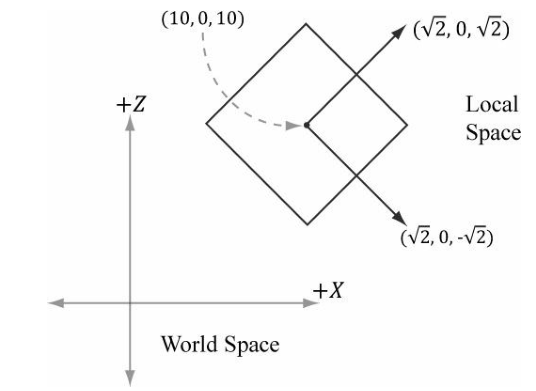
W = [\begin{matrix} u_{x} & u_{y} & u_{z} & 0 \\ v_{x} & v_{y} & v_{z} & 0 \\ w_{x} & w_{y} & w_{z} & 0 \\ Q_{x} & Q_{y} & Q_{z} & 1 \end{matrix}]

$W=\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ w_x & w_y & w_z & 0 \\ Q_x & Q_y & Q_z & 1 \\ \end{bmatrix}$

其中，[ux, uy, uz, 0]，[vx, vy, vz, 0]和[wx, wy, wz, 0] 表示局部坐标系三个相互垂直的轴向量（这三个向量的模不一定相等），而[Qx, Qy, Qz, 1]则表示上述坐标轴原点在世界坐标系的位置坐标。这种表示形式的世界变换矩阵也可以理解为局部坐标系在世界坐标系的位置，以及三个轴向量在世界坐标系的表现形式。现在对一个物体进行缩放、顺时针旋转、平移：

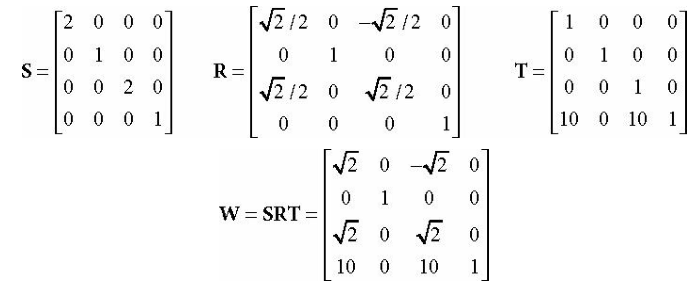
变换结果如下：

观察空间

为了获取一个2D图像，我们必须引入虚拟摄像机的概念。一个虚拟摄像机可以看作一个观察坐标系，它也是一个局部坐标系，原点为摄像机的位置，Z轴为摄像机的观察方向，Y轴为摄像机的上方向，而X轴则为摄像机的右方向。

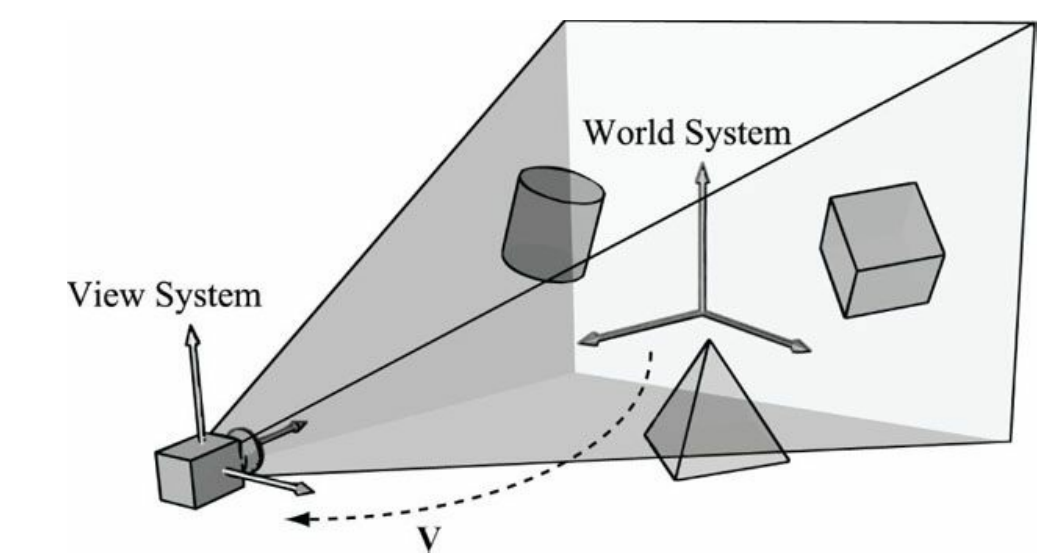
若已知[ux, uy, uz, 0]，[vx, vy, vz, 0]和[wx, wy, wz, 0]分别对应观察坐标系的三个相互垂直的单位坐标轴，以及[Qx, Qy, Qz, 1]表示摄像机在世界坐标系的位置，那么从观察坐标系到世界坐标系的世界变换矩阵如下：

W = R T = [\begin{matrix} u_{x} & u_{y} & u_{z} & 0 \\ v_{x} & v_{y} & v_{z} & 0 \\ w_{x} & w_{y} & w_{z} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ Q_{x} & Q_{y} & Q_{z} & 1 \end{matrix}] = [\begin{matrix} u_{x} & u_{y} & u_{z} & 0 \\ v_{x} & v_{y} & v_{z} & 0 \\ w_{x} & w_{y} & w_{z} & 0 \\ Q_{x} & Q_{y} & Q_{z} & 1 \end{matrix}]

$\mathbf{W}=\mathbf{RT}=\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ w_x & w_y & w_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ Q_x & Q_y & Q_z & 1 \\ \end{bmatrix}=\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ w_x & w_y & w_z & 0 \\ Q_x & Q_y & Q_z & 1 \\ \end{bmatrix}$

然而，我们想做的并不是这样，现在我们想要的是从世界坐标系转换到观察（局部）坐标系。逆变换可以由变换矩阵的逆求得，所以从世界空间到观察空间的坐标变换矩阵为W^-1

V = W^{- 1} = (R T)^{- 1} = T^{- 1} R^{- 1} = T^{- 1} R^{T} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - Q_{x} & - Q_{y} & - Q_{z} & 1 \end{matrix}] [\begin{matrix} u_{x} & v_{x} & w_{x} & 0 \\ u_{y} & v_{y} & w_{y} & 0 \\ u_{z} & v_{z} & w_{z} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} u_{x} & v_{x} & w_{x} & 0 \\ u_{y} & v_{y} & w_{y} & 0 \\ u_{z} & v_{z} & w_{z} & 0 \\ - Q_{x} \cdot u & - Q_{y} \cdot v & - Q_{z} \cdot w & 1 \end{matrix}]

$\mathbf{V}=\mathbf{W^{-1}}=\mathbf{(RT)^{-1}}=\mathbf{T^{-1}R^{-1}}=\mathbf{T^{-1}R^T}= \\ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -Q_x & -Q_y & -Q_z & 1 \\ \end{bmatrix}\begin{bmatrix} u_x & v_x & w_x & 0 \\ u_y & v_y & w_y & 0 \\ u_z & v_z & w_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}=\begin{bmatrix} u_x & v_x & w_x & 0 \\ u_y & v_y & w_y & 0 \\ u_z & v_z & w_z & 0 \\ -Q_x\cdot \mathbf{u} & -Q_y\cdot \mathbf{v} & -Q_z\cdot \mathbf{w} & 1 \\ \end{bmatrix}$

现在我们来展示一种用于构建观察矩阵中所有向量的直观方法。若已知Q为摄像机的位置，T为摄像机对准的观察目标点，j为世界空间“向上”方向的单位向量。（下图以平面xOz作为场景中的“地平面”，并以世界空间的y轴作为摄像机“向上”的方向。因此，j=(0,1,0)仅是平行于世界空间中y轴的一个单位向量）对于下图来说，虚拟摄像机的观察方向为：

w = \frac{T - Q}{∥ T - Q ∥}

$\mathbf{w}=\frac{\mathbf{T-Q}}{\parallel\mathbf{T-Q}\parallel}$

该向量表示虚拟摄像机局部空间的z轴。指向w“右侧”的单位向量为：

u = \frac{j \times w}{∥ j \times w ∥}

$\mathbf{u}=\frac{\mathbf{j}\times\mathbf{w}}{\parallel\mathbf{j}\times\mathbf{w}\parallel}$

它表示的是虚拟摄像机局部空间的x轴。最后，该摄像机局部空间的y轴为：

v = w \times u

$\mathbf{v}=\mathbf{w}\times\mathbf{u}$

因为w和u是互相正交的单位向量，所以v也必为单位向量。因此我们也无须对向量v进行规范化处理了。

DirectXMath库针对上述计算观察矩阵的处理流程提供了以下函数：

XMMATRIX XMMatrixLookAtLH(  // 输出视图变换矩阵V
    FXMVECTOR EyePosition,      // 输入摄影机坐标
    FXMVECTOR FocusPosition,    // 输入摄影机焦点坐标
    FXMVECTOR UpDirection);     // 输入摄影机上朝向坐标

投影变换

最近在看GAMES101: 现代计算机图形学入门，对投影矩阵这边有了新的见解。故在这里翻新一下内容。

投影变换的目的就是要将3D的场景投影到一个2D的平面上。包含透视投影和正交投影两种。其中由透视投影产生的图片中的物体会表现为近大远小，而正交投影产生的图片中的物体只与他本身的大小有关，与距离无关。

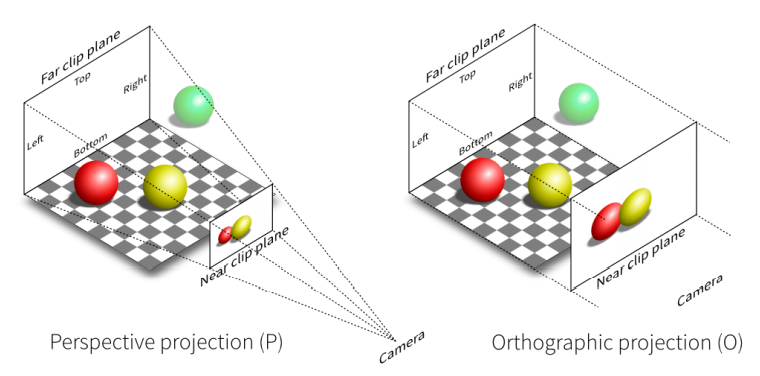
正交投影变换与标准化设备坐标（NDC）

由于正交投影变换相对简单，放在这里先讲，也为了引出后面的内容。

在经过观察变换后，此时我们来到了摄像机的局部空间，即摄像机位于原点，朝着+Z方向观察，上方向为+Y。我们要在这个基础上定义投影范围。观察上图，可以看到正交投影的可视范围是一个长方体，而且它是与坐标轴对齐的。我们可以对这个立方体进行平移，或者是缩放。只要物体落在立方体内且没有被遮挡，则最终投影出来的2D图片上我们是可以看到它的。

而对于硬件来说，使用统一的标准化设备坐标，可以无需提前知道屏幕的宽高比来简化像素的映射操作。坐标点在经过正交投影后，w的值会保持为1。这时候NDC空间的可视取值范围为：

- 1 \leq x \leq 1 - 1 \leq y \leq 1 0 \leq z \leq 1 w = 1

$-1\leq x\leq 1\\ -1\leq y\leq 1\\ 0\leq z\leq 1\\ w=1$

这个范围正好也是表示一个立方体。有了这个区间范围，我们可以将它再变换到任意大小和位置的2D矩形上。这个变换过程叫视口变换。

现在我们尝试求出以原点为中心的正交投影矩阵。定义可视立方体的宽度为w，高度为h，近平面位于z=n，远平面位于z=f.

[\begin{matrix} \frac{w}{2} & \frac{h}{2} & n & 1 \end{matrix}] P_{o r t h o} = [\begin{matrix} 1 & 1 & 0 & 1 \end{matrix}] [\begin{matrix} 0 & 0 & f & 1 \end{matrix}] P_{o r t h o} = [\begin{matrix} 0 & 0 & 1 & 1 \end{matrix}]

$\begin{bmatrix} \frac{w}{2} & \frac{h}{2} & n & 1 \end{bmatrix} P_{ortho} = \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \\ \begin{bmatrix} 0 & 0 & f & 1 \end{bmatrix} P_{ortho} = \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \\$

由于x和y只受缩放影响，而w始终都未发生变化，故正交投影矩阵的这些参数都可以确定下来：

P_{o r t h o} = [\begin{matrix} \frac{2}{w} & 0 & ? & 0 \\ 0 & \frac{2}{h} & ? & 0 \\ 0 & 0 & ? & 0 \\ 0 & 0 & ? & 1 \end{matrix}]

$P_{ortho}=\begin{bmatrix} \frac{2}{w} & 0 & ? & 0 \\ 0 & \frac{2}{h} & ? & 0 \\ 0 & 0 & ? & 0 \\ 0 & 0 & ? & 1 \\ \end{bmatrix}$

现在观察这两个式子：

[\begin{matrix} \frac{w}{2} & \frac{h}{2} & n & 1 \end{matrix}] [\begin{matrix} ? \\ ? \\ ? \\ ? \end{matrix}] = 0 [\begin{matrix} 0 & 0 & f & 1 \end{matrix}] [\begin{matrix} ? \\ ? \\ ? \\ ? \end{matrix}] = 1

$\begin{bmatrix} \frac{w}{2} & \frac{h}{2} & n & 1 \end{bmatrix} \begin{bmatrix} ? \\ ? \\ ? \\ ? \end{bmatrix} = 0\\ \begin{bmatrix} 0 & 0 & f & 1 \end{bmatrix} \begin{bmatrix} ? \\ ? \\ ? \\ ? \end{bmatrix} = 1\\$

坐标点与第三行相乘的结果是向量的z值，而上面的方程得到的z值都是常数，显然与w和h无关。故第一行和第二行都是0，然后我们设第三行和第四行的分别为A和B

P_{o r t h o} = [\begin{matrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 & 0 \\ 0 & 0 & A & 0 \\ 0 & 0 & B & 1 \end{matrix}]

$P_{ortho}=\begin{bmatrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 & 0 \\ 0 & 0 & A & 0 \\ 0 & 0 & B & 1 \\ \end{bmatrix}$

由：

n A + B = 0 f A + B = 1

$nA+B=0\\ fA+B=1$

解得：

A = \frac{1}{f - n} B = \frac{- n}{f - n}

$A=\frac{1}{f-n}\\ B=\frac{-n}{f-n}$

故以原点为中心的正交投影矩阵构造如下：

P_{o r t h o} = [\begin{matrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{- n}{f - n} & 1 \end{matrix}]

$P_{ortho}=\begin{bmatrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{-n}{f - n} & 1 \\ \end{bmatrix}$

经过投影矩阵变换后的深度值依然保持线性关系：

G (z) = \frac{z}{f - n} + \frac{- n}{f - n}

$G(z)=\frac{z}{f-n}+\frac{-n}{f-n}$

在DirectXMath中，对应的函数为XMMatrixOrthographicLH：

XMMATRIX XMMatrixOrthographicLH(
    float ViewWidth,	// [In]待投影区域的宽度 
    float ViewHeight, 	// [In]待投影区域的高度
    float NearZ, 		// [In]近平面
    float FarZ);		// [In]远平面

而对于离心的正交投影矩阵，无非就是在上面的正交投影的基础上再将其平移回中心位置上。若规定投影立方体为[left, right] x [bottom, top] x [n, f]，则有：

P_{o r t h o} = [\begin{matrix} \frac{2}{r i g h t - l e f t} & 0 & 0 & 0 \\ 0 & \frac{2}{t o p - b o t t o m} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ - \frac{r i g h t + l e f t}{r i g h t - l e f t} & - \frac{t o p + b o t t o m}{t o p - b o t t o m} & \frac{- n}{f - n} & 1 \end{matrix}]

$P_{ortho}=\begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ -\frac{right+left}{right-left} & -\frac{top+bottom}{top-bottom} & \frac{-n}{f - n} & 1 \\ \end{bmatrix}$

left和right指定投影区域的左右边界，top和bottom指定投影区域的上下边界。

在DirectXMath中，对应的函数为XMMatrixOrthographicOffCenterLH：

XMMATRIX XMMatrixOrthographicOffCenterLH(
    float ViewLeft,		// [In]待投影区域的左边界 
    float ViewRight, 	// [In]待投影区域的右边界
    float ViewBottom, 	// [In]待投影区域的下边界
    float ViewTop, 		// [In]待投影区域的上边界
    float NearZ, 		// [In]近平面
    float FarZ);		// [In]远平面

按像素定义世界空间的优点是能够做到按像素绘制到屏幕上，但缺点是不允许出现像素的拉伸，如果屏幕分辨率被改变，那投影区域也应当随之改变。

透视投影变换

讲完正交投影，接下来是投影变换。由下图可知，在不限制远近范围的情况下，摄像机的视野就像是一个无限延伸的四棱锥。

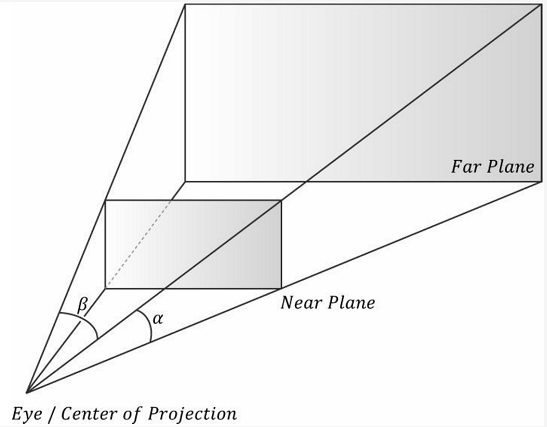
和正交投影一样，我们也需要定义近平面和远平面来限制范围，那定义出来的可视范围实际上就是一个平截头体（或叫视锥体更方便一些）。

不过这个视锥体对我们来说并不好处理，最好是想办法把这个视锥体给挤压成一个正交立方体，然后再进行正交投影变换。

将视锥体挤压成正交立方体

现在我们以yOz平面的视角来观察这个视锥体。在视锥体上有一点(x, y, z)，由于透视投影相当于从摄像机发射出一系列射线，射线上的任意一点都会投影到屏幕的同一高度位置上，故同样高度的物体在近处显得高，在远处则显得较矮。根据相似三角形的性质，我们可以求出(x,y,z)投影到平面z=n的位置为(x', y', n)。其中：

x^{'} = \frac{x n}{z} y^{'} = \frac{y n}{z}

$x'=\frac{xn}{z}\\ y'=\frac{yn}{z}\\$

然而我们用矩阵乘法并不能帮我们进行除z这一操作。我们需要利用前面提到的齐次坐标的性质进行扩维，把(x, y, z)变成(x, y, z, 1)，那么(xz, yz, z^2, z)和前者也表示同一个顶点。即便是这样，我们也不好用一个四维矩阵变换得到，因为我们需要的这个投影矩阵是一个与x, y, z无关的矩阵。

因此我们可以这样做。首先令z=n，然后取近平面上一点(x, y, n, 1)，那么(xn, yn, n^2, n)同样也表示这个点，且近平面上的点投影到近平面依然是它本身（即没有产生挤压）。因此有：

[\begin{matrix} x & y & n & 1 \end{matrix}] P_{p e r s p \to o r t h o} = [\begin{matrix} x n & y n & n^{2} & n \end{matrix}]

$\begin{bmatrix} x & y & n & 1 \end{bmatrix} P_{persp\rightarrow ortho} = \begin{bmatrix} xn & yn & n^2 & n \end{bmatrix}$

由于x和y都是被缩放的，故只有它们对应的主元是n。对于w分量，我们这里让第四列的第三行为1，而不是让第四行的为n，原因在下面会提到。

P_{p e r s p \to o r t h o} = [\begin{matrix} n & 0 & ? & 0 \\ 0 & n & ? & 0 \\ 0 & 0 & ? & 1 \\ 0 & 0 & ? & 0 \end{matrix}]

$P_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & ? & 0 \\ 0 & n & ? & 0 \\ 0 & 0 & ? & 1 \\ 0 & 0 & ? & 0 \\ \end{bmatrix}$

现在再令z=f，点(x, y, f)会被挤压成(xn/f, yn/f, f) （只有x和y才会被挤压），而在齐次坐标系中(xn/f, yn/f, f, 1)和(xn, yn, f^2, f)又是同一个点。因此可以有：

[\begin{matrix} x & y & f & 1 \end{matrix}] P_{p e r s p \to o r t h o} = [\begin{matrix} x n & y n & f^{2} & f \end{matrix}]

$\begin{bmatrix} x & y & f & 1 \end{bmatrix} P_{persp\rightarrow ortho} = \begin{bmatrix} xn & yn & f^2 & f \end{bmatrix}$

结合这两个方程，我们就可以知道这里只能让第四列的第三行为1。

现在观察z分量的变换：

[\begin{matrix} x & y & n & 1 \end{matrix}] [\begin{matrix} ? \\ ? \\ ? \\ ? \end{matrix}] = n^{2} [\begin{matrix} x & y & f & 1 \end{matrix}] [\begin{matrix} ? \\ ? \\ ? \\ ? \end{matrix}] = f^{2}

$\begin{bmatrix} x & y & n & 1 \end{bmatrix} \begin{bmatrix} ? \\ ? \\ ? \\ ? \end{bmatrix} = n^2\\ \begin{bmatrix} x & y & f & 1 \end{bmatrix} \begin{bmatrix} ? \\ ? \\ ? \\ ? \end{bmatrix} = f^2\\$

显然x和y对结果并不会有影响，故可以确定第一行和第二行为0。此时可以令第三行和第四行分别设为A和B，则有：

P_{p e r s p \to o r t h o} = [\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & 1 \\ 0 & 0 & B & 0 \end{matrix}]

$P_{persp\rightarrow ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & 1 \\ 0 & 0 & B & 0 \\ \end{bmatrix}$

由：

n A + B = n^{2} f A + B = f^{2}

$nA+B=n^2\\fA+B=f^2$

解得：

A = n + f B = - f n

$A=n+f\\B=-fn$

故将视锥体挤压成正交立方体（由透视到正交的变换）的矩阵如下：

P_{p e r s p \to o r t h o} = [\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & 1 \\ 0 & 0 & - f n & 0 \end{matrix}]

$P_{persp\rightarrow ortho}= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & 1 \\ 0 & 0 & -fn & 0 \\ \end{bmatrix}$

这个矩阵用图表现起来就像这样：

但经过该矩阵变换后得到的深度值显然不是线性的。

G (z) = A + \frac{B}{z}

$G(z)=A+\frac{B}{z}$

关于深度值的变换函数，等最终的透视投影矩阵求出来后再讨论。

垂直视场角（FOV）和宽高比（Aspect Ratio）

前面那个矩阵只是帮助我们将分散的射线挤压成平行的射线（前提是n > 0），但我们还没确定这个正交投影的范围。虽然用[l, r]x[b, t]x[n, f]可以得到投影矩阵，但仍然不是很方便。我们需要引入两个新的变量来间接进行描述。

垂直视场角（FOV）是指视锥体垂直方向的最大夹角。这就变相定义了这个视锥体近平面的高度了：

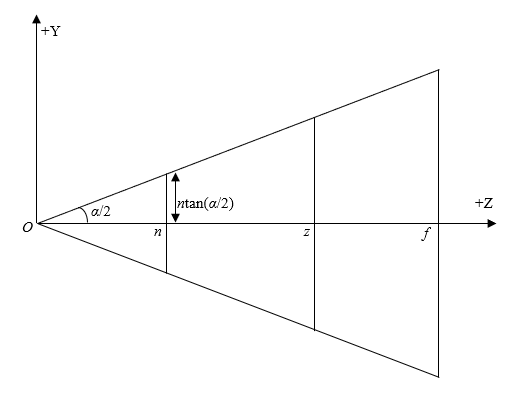
近平面高度为：

h = 2 n \cdot t a n (α / 2)

$h=2n\cdot tan(\alpha/2)$

然后通过宽高比（AspectRatio）把视锥体近平面宽度（同时也是正交立方体的宽高）也确定出来。令宽高比为r,则：

r = w / h w = 2 r n \cdot t a n (α / 2)

$r=w/h \\ w = 2rn\cdot tan(\alpha / 2)$

代入到正交投影矩阵有：

P_{o r t h o} = [\begin{matrix} \frac{1}{r n \cdot t a n (α / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{n \cdot t a n (α / 2)} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{- n}{f - n} & 1 \end{matrix}]

$P_{ortho}=\begin{bmatrix} \frac{1}{rn\cdot tan(\alpha/2)} & 0 & 0 & 0 \\ 0 & \frac{1}{n\cdot tan(\alpha/2)} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{-n}{f - n} & 1 \\ \end{bmatrix}$

故最终的透视投影矩阵为：

\begin{aligned} (1) & P_{p e r s p} & = P_{p e r s p \to o r t h o} P_{o r t h o} \\ (2) & = [\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & 1 \\ 0 & 0 & - f n & 0 \end{matrix}] [\begin{matrix} \frac{1}{r n \cdot t a n (α / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{n \cdot t a n (α / 2)} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{- n}{f - n} & 1 \end{matrix}] \\ (3) & = [\begin{matrix} \frac{1}{r t a n (α / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{t a n (α / 2)} & 0 & 0 \\ 0 & 0 & \frac{f}{f - n} & 1 \\ 0 & 0 & - \frac{n f}{f - n} & 0 \end{matrix}] \end{aligned}

$\begin{align} P_{persp}&=P_{persp\rightarrow ortho} P_{ortho} \\ &= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & 1 \\ 0 & 0 & -fn & 0 \\ \end{bmatrix}\begin{bmatrix} \frac{1}{rn\cdot tan(\alpha/2)} & 0 & 0 & 0 \\ 0 & \frac{1}{n\cdot tan(\alpha/2)} & 0 & 0 \\ 0 & 0 & \frac{1}{f - n} & 0 \\ 0 & 0 & \frac{-n}{f - n} & 1 \\ \end{bmatrix} \\ &= \begin{bmatrix} \frac{1}{rtan(\alpha/2)} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\alpha/2)} & 0 & 0 \\ 0 & 0 & \frac{f}{f-n} & 1 \\ 0 & 0 & -\frac{nf}{f-n} & 0 \\ \end{bmatrix} \end{align}$

归一化深度值、Direct3D裁剪范围

齐次裁剪空间、归一化深度

待投影操作完毕后，所有经过透视投影变换后的点[x, y, z, w] 被变换到了齐次裁剪空间。顾名思义，光栅化期间需要对所有位于齐次裁剪空间的顶点进行裁剪判定，具体为：

- w \leq x \leq w - w \leq y \leq w 0 \leq z \leq w 0 < w

$-w\leq x\leq w\\ -w\leq y\leq w\\ 0\leq z\leq w\\ 0<w$

我们要特别留意这个 $w>0$ 项，因为这个w实际上是处于观察空间的深度值，显然w不应该小于等于0，否则 $0\leq z\leq w$ 就没有意义了，并且透视除法后w会被归一化了。正交投影时 $w=1$ ，和前面的范围是对得上的。在完成裁剪后，光栅化阶段就会进行透视除法，对整个顶点向量除以w使得深度值能够归一化。经过透视除法后的顶点此时才真正的来到了NDC空间。重新梳理一遍，物体的空间变换过程为：

局部空间→世界空间→观察空间→齐次裁剪空间→标准化设备空间

分别对应的是：世界矩阵变换、观察矩阵变换、透视矩阵变换、透视除法

当透视矩阵为正交时，所处的齐次裁剪空间与标准化设备空间是一致的，因为w=1

然后我们来看看深度值是如何进行归一化的。首先，我们必须构建一个保序函数g(z)，用来把z坐标从[n, f]映射到区间[0, 1]。由于该函数具有保序性，即如果 $z_1, z_2 \in [n, f]$ 且 $z_1<z_2$ ，那么 $g(z_1)<g(z_2)$ 。也就是说，对深度值进行归一化处理后，深度关系保持不变。所以，在实现深度缓冲算法的过程中，我们仍能在归一化区间内正确地比较出不同点之间的深度关系。

虽然通过一次缩放和平移操作，便能将z坐标从[n, f]区间映射到[0, 1]区间。但是此方法却不能整合到我们当前的投影方案中去。在上式中，z坐标经过了以下变换的处理：

g (z) = \frac{f}{f - n} - \frac{n f}{(f - n) z}

$g(z)=\frac{f}{f-n}-\frac{nf}{(f-n)z}$

根据函数g(z)的图像可以看出，它是严格递增（保序性）的非线性函数。同时，这也反映了g(z)大部分取值是由近平面附近的深度值所计算得出的。换言之，大多数的深度值被集中地映射到了取值区间中的一段较小的区域内。这将引发深度缓冲区的精度问题（由于计算机表示的数值范围有限，使计算机不足以区分归一化深度值之间的微小差异）。对此，我们一般建议令近平面与远平面尽可能地接近，以改善深度值的问题。

紧接着还需要对透视除法后的坐标进行插值运算，由于g(z)函数是非线性的，使用线性插值法对深度的插值会出现问题。这就需要使用透视校正插值法来计算出正确的深度值，有兴趣的话作为练习题自行了解。

在DirectXMath中，我们使用下面的函数来获得一个投影矩阵：

XMMATRIX XMMatrixPerspectiveFovLH( // 返回投影矩阵
    FLOAT FovAngleY,                   // 中心垂直弧度
    FLOAT AspectRatio,                 // 宽高比
    FLOAT NearZ,                       // 近平面距离
    FLOAT FarZ);                       // 远平面距离

回到顶部

2D的变换与投影成像

Direct3D不仅能够绘制3D物体，还可以在后备缓冲区直接绘制2D平面物体。当然，也可以使用Direct2D来绘制2D物体（后续章节会涉及到Direct2D与Direct3D的交互）。

我们也可以借助3D绘制的思想，划分为世界变换、可脱离中心的正交投影变换（也可以细分成摄像机变换、以原点为中心的正交投影变换）、视口变换。

考虑有人可能会跳过3D部分来看2D，这里在内容上和3D会有些重复。

2D局部空间与2D世界空间

由于是2D世界空间，通常只有x轴和y轴会利用到，绝大部分情况下我们可以让z值等于0。

和3D物体一样，每个2D物体都有其自己的2D局部空间（局部坐标系），但是2D世界空间只有一个。

2D世界变换也囊括了缩放、旋转和平移变换。通过世界变换，我们可以将物体模型从自身的局部坐标系转换到世界坐标系中。当然，我们也可以理解为将物体从世界原点开始缩放、旋转，然后平移到目标位置。这样每一个物体都能在同一个世界空间中表示。

注意：对于不同的物体，需要使用不同的世界变换矩阵；而对于同一个顶点的所有顶点，都要使用一致的世界变换矩阵来变换。

从局部空间到世界空间的坐标变换矩阵即为前面提到的：

W = [\begin{matrix} u_{x} & u_{y} & 0 & 0 \\ v_{x} & v_{y} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ Q_{x} & Q_{y} & 0 & 1 \end{matrix}]

$W=\begin{bmatrix} u_x & u_y & 0 & 0 \\ v_x & v_y & 0 & 0 \\ 0 & 0 & 1 & 0 \\ Q_x & Q_y & 0 & 1 \\ \end{bmatrix}$

对于旋转矩阵，我们只使用XMMatrixRotationZ。

正交投影变换与标准化设备坐标（NDC）

正如前面所说的，标准化设备坐标的可视取值范围为：

- 1 \leq x \leq 1 - 1 \leq y \leq 1 0 \leq z \leq 1 w = 1

$-1\leq x\leq 1\\ -1\leq y\leq 1\\ 0\leq z\leq 1\\ w=1$

其中z值被用于深度测试，我们可以利用z值给2D绘制划分出更多的层次，比如说把场景分成16层，这样z根据层级从最优先到最后可以依次设置为0, 1/15, ... , 1。

在知道了最终的可视范围后，我们该如何定义世界空间的长度呢？

一种做法是按像素来定义，即我们可以定义1个像素的宽高作为1个单位的x值和y值。这样当观察中心位于原点时，在分辨率为800x600的情况下四个可视边界点分别为(-400, -300), (-400, 300), (400, 300), (400, -300)。然后我们需要使用正交投影变换（由函数XMMatrixOrthographicLH获取），将x∈[-400, 400], y∈[-300, 300]的区间映射到NDC的可视范围内。

如果你的游戏世界很大，超出一个屏幕，想要获取离开屏幕中心区域的投影的话，可以使用下面带平移的正交投影矩阵（由函数XMMatrixOrthographicOffCenterLH获取）：left和right指定投影区域的左右边界，top和bottom指定投影区域的上下边界。

按像素定义世界空间的优点是能够做到按像素绘制到屏幕上，但缺点是不允许出现像素的拉伸，如果屏幕分辨率被改变，那投影区域也应当随之改变。

如果你不打算按像素定义，也可以自己定义游戏内的世界尺度，比如可视游戏区域的范围为宽200个单位，高150个单位。那么投影矩阵的宽需要固定在200个单位，高需要固定在150个单位。这种做法如果允许窗口被拉伸的话，那么游戏场景也将被拉伸，若要拉伸最好是等比例的拉伸。

注意：基于NDC的x轴朝右，y轴朝上，而你自己定义的世界坐标系可能是x轴朝右，y轴朝下。这需要进行一个负向的投影变换。

回到顶部

HLSL变量命名的一些约定

在阅读HLSL代码的时候你将会遇到诸如PosW、PosH这样带字母后缀的变量名，那么它们有什么含义呢？其实该字母表达了当前点或向量所处的空间：

字母后缀	含义
L	处于物体局部空间（Local Space）
W	处于世界空间（World Space）
V	处于观察空间（View Space）
H	处于齐次裁减空间（Homogeneous space）

回到顶部

练习题

粗体字为自定义题目

若有兴趣，可以去了解一下绕任意轴旋转的矩阵推导过程。本章不列出。
若有兴趣，可以去了解一下透视校正插值法。本章不列出。
修改项目03，在窗口被拉伸的情况下修改透视投影矩阵的宽高比保证物体正常显示。
修改项目03，观察透视投影矩阵下不同FOV值的效果，以及将远平面设置为5.0f的效果
修改项目03，让摄像机位于点(1, 0, -2)观察原点，并使用正交投影观察效果
修改项目03，让立方体中心位于点(3, 0, 0)，然后立方体按Z轴绕原点逆时针旋转，同时它也按Z轴绕立方体中心顺时针旋转，速度自拟。

DirectX11 With Windows SDK完整目录

Github项目源码

欢迎加入QQ群: 727623616 可以一起探讨DX11，以及有什么问题也可以在这里汇报。

posted @ 2017-07-26 20:54 X_Jun 阅读(11215) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

阅读排行：
· 震惊！C++程序真的从main开始吗？99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码？零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾（3.3-3.9）
· winform 绘制太阳，地球，月球运作规律

X_Jun

DirectX11 With Windows SDK--04 变换

前言

Direct3D的一些规定

3D坐标系

纹理坐标系和屏幕坐标系

矩阵计算

矩阵变换

基、基向量

变换矩阵

线性变换

缩放

旋转

仿射变换

齐次坐标

仿射变换的定义及矩阵表示

平移

变换的复合

坐标变换

3D的变换与投影成像

局部空间与世界空间

观察空间

投影变换

正交投影变换与标准化设备坐标（NDC）

透视投影变换

将视锥体挤压成正交立方体

垂直视场角（FOV）和宽高比（Aspect Ratio）

归一化深度值、Direct3D裁剪范围

齐次裁剪空间、归一化深度

2D的变换与投影成像

2D局部空间与2D世界空间

正交投影变换与标准化设备坐标（NDC）

HLSL变量命名的一些约定

练习题

公告

我的标签

积分与排名

随笔分类

阅读排行榜

推荐排行榜

最新评论