【论文笔记】Learning to Estimate 3D Human Pose and Shape from a Single Color Image(CVPR 2018)
这篇论文没有给出代码，细节部分还是得看论文来推敲了，因此可能会有理解出问题的地方。
概述
做了什么：引入一个端到端的框架，从包含人体的单张RGB图像中预测出轮廓图和关节热力图，生成SMPL参数并重建出一个SMPL的3D人体网格
存在问题：卷积网络容易受到缺少训练数据、3D预测时分辨率低的影响
关键点：提出了一个基于卷积网络的高效的直接预测方法来解决上面的问题
特点：
- 端到端网络的输出用于预测SMPL模型的参数
- 从参数生成3D网格的过程是可微的，可以添加到网络中
- 投影过程也是可微的，意味着投影过程也可以训练
模型
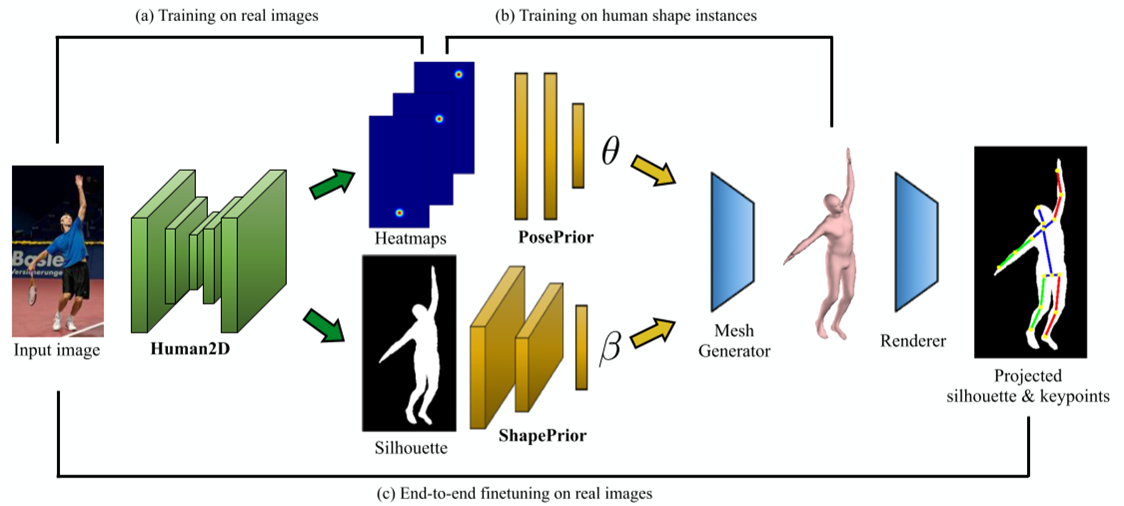
- Human2D：使用stacked-hourglass模型，对输入图像处理得到关节热力图与轮廓图
- SMPL参数生成：PosePrior是全连接层，对热力图处理后得到SMPL的θ参数；ShapePrior则是卷积层与全连接层，对轮廓图处理后得到SMPL的β参数
- Mesh Generator： 可微SMPL生成函数，作为网络的一部分，没有可学习的参数
- Renderer： 投影矩阵是可微的，通过学习得到，将SMPL模型投影后可生成轮廓图和关节点图像
Human2D
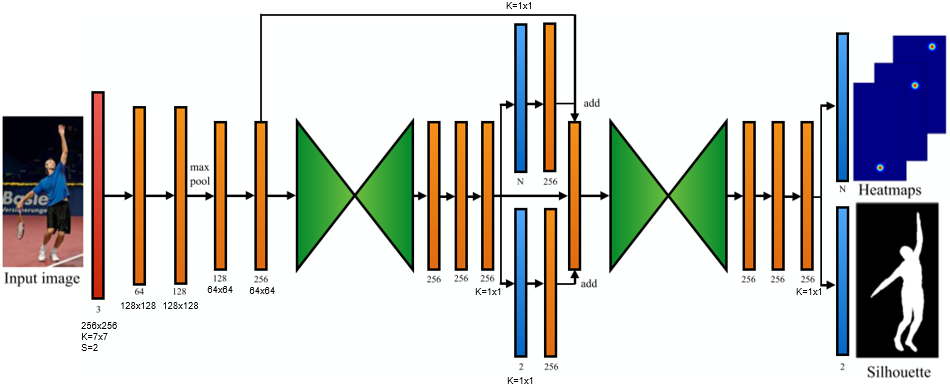
输入图像分辨率为256x256
其中红色部分为7x7的卷积层，步幅为2
橙色部分为3x3的卷积层，下面黑字为通道数，再下面是卷积前的宽高。但是用于产生蓝色结果的卷积以及在它之后进行后处理的卷积使用的是1x1的核
绿色部分则为hourglass部分
蓝色部分为输出的关节点热力图或者轮廓图（分辨率都是64x64），热力图通道数即为关节点数目，轮廓图通道数为2（分人体和背景）
Hourglass
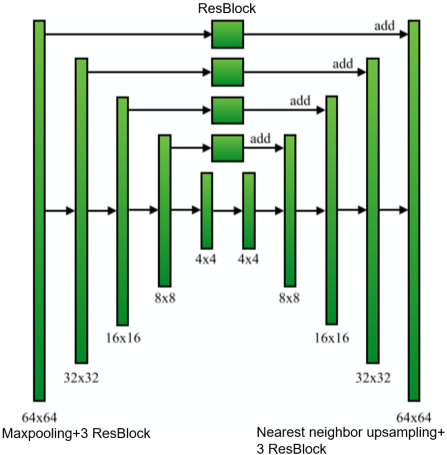
每一列绿色块对应3个连续的残差块。卷积核采用3x3，并且通道数在hourglass中保持在256个，使用了ReLU激活函数和Bath normalization。在encoding部分，使用max pooling来降采样;在decoding部分，使用nearest neighbor upsampling上采样。跳接层通用也包含残差块，它们的输出将会按元素加进上采样后decoding部分的特征图
Human2D Losses
\(L_{hm}\)：使用网络输出的关节点热力图与ground-truth的关节图采用逐像素的MSE Loss
\(L_{sil}\)：使用网络输出的轮廓图与ground-truth的轮廓图采用逐像素的二进制交叉熵
\(L_{hg}=\lambda L_{hm} + L_{sil}, \lambda=100\)
PosePrior
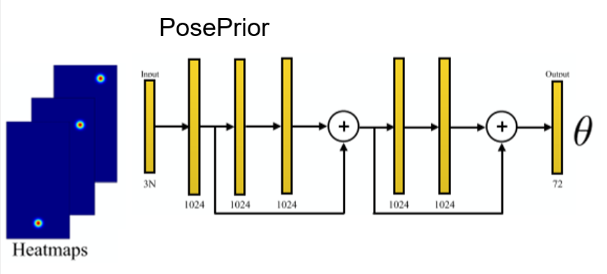
在热力图中，找到置信度最大的像素位置，组合成(x, y, confidence)，然后N个关节点就有3N个特征，每个1024全连接层后面使用BatchNorm、ReLu、Dropout
ShapePrior
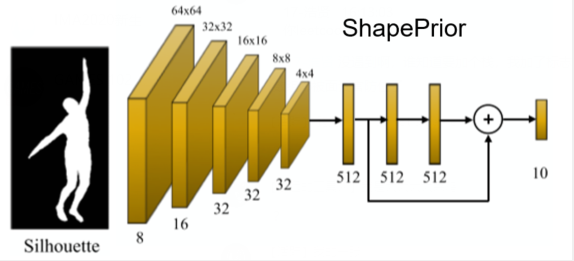
在3x3卷积后使用max pooling，每个1024全连接层后面使用BatchNorm、ReLu、Dropout
利用SMPL生成ground-truth
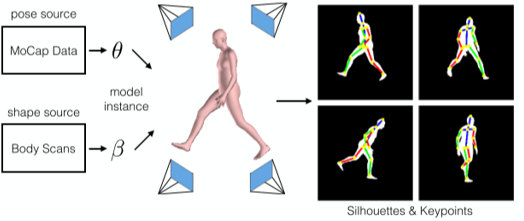
可以使用MoCap Data产生姿势参数，Body Scans产生体型参数，然后传递给SMPL，再通过不同的视图投影网格模型和关节点来制作轮廓图和关节点热力图，作为ground-truth
Mesh Generator
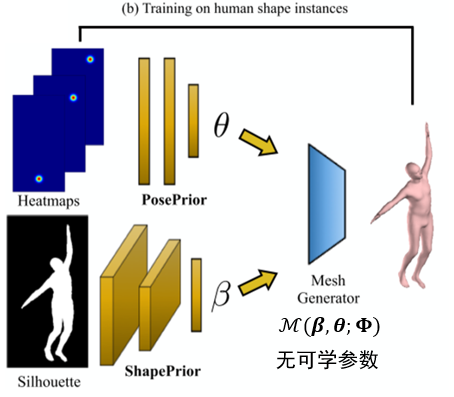
SMPL模型的生成过程变成了网络的一部分，即这部分过程也是可微的。
在训练时，首先针对Prior网络使用L2参数Loss完成初始学习，然后再经过Mesh Generator生成3D关节点和顶点的方式，固定其中一个Prior网络，使用下述Loss来fine-tuning另一个网络的参数。
损失函数：
- 3D per-vertex loss：\(L_M = \sum_{i=1}^{N} \parallel \hat{P_i}-\hat{P_i}\parallel_2^2, N=6890\)
- 3D joint loss：\(L_J=\sum_{i=1}^{M} \parallel \hat{J_i}-\hat{J_i}\parallel_2^2, M=23\)
Renderer
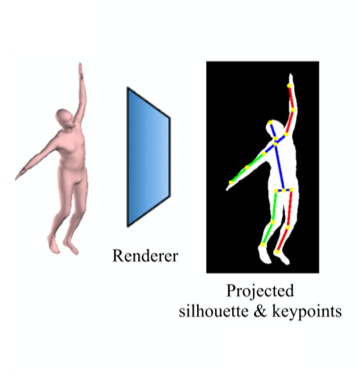
将3D关节点和顶点都投影到图片上得到2D关节点和2D顶点
\(\Pi(\hat{P})=\hat{S}, \Pi(\hat{J})=\hat{W}\)
\(L_{\Pi}=\mu\sum_{i}^{M}\parallel\hat{W_i}-\hat{W_i}\parallel_2^2+\parallel\hat{S_i}-\hat{S_i}\parallel_2^2, \mu=10\)
而投影过程是可微的，所以可以通过学习得到
实验
测试数据集：UP-3D、SURREAL(CMU)
测试指标：mean per-vertex errors
消融实验
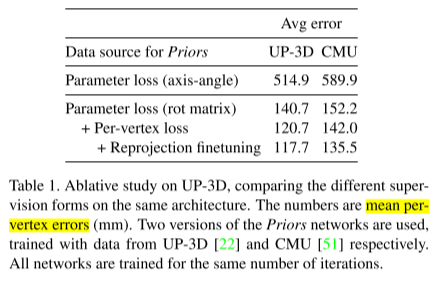
对UP-3D进行消融实验，若使用轴角表示法来训练Priors，造成的误差会非常大。因为轴角表示法在某些情况下并不是唯一的，不易于收敛。采用罗德里格旋转矩阵表示法的话旋转表示是唯一的，因此误差可以降低很多。而通过生成模型进行顶点的比对3D顶点L2损失，以及再重投影回到图象空间来比对2D顶点L2损失，都可以对实验结果有更细微的改善
UP-3D对比
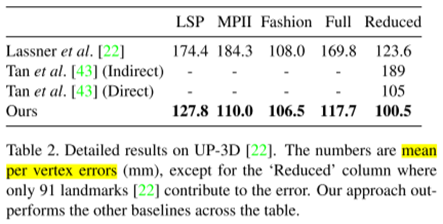
部件分割
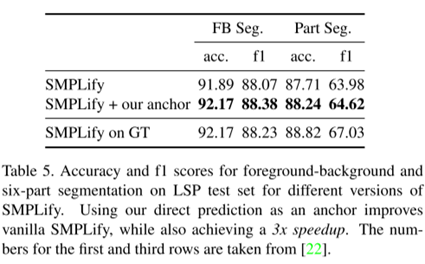
更多实验细节可以去阅读原文以及补充材料。
