编译原理--04 符号表、运行时存储组织和代码优化复习(清华大学出版社第3版)
前言
| 目录 |
|---|
| 01 文法和语言、词法分析复习 |
| 02 自顶向下、自底向上的LR分析复习 |
| 03 语法制导翻译和中间代码生成复习 |
| 04 符号表、运行时存储组织和代码优化复习 |
| 05 用C++手撕PL/0 |
第8章 静态语义分析和中间代码生成(续)
符号表
符号表需要在编译期间用到,记录符号的具体信息。本部分只讨论PL/0符号表的建立。
PL/0符号表结构
PL/0的符号表包含5个信息:
- NAME,符号名
- KIND,符号类型
- LEVEL/VAL,层次/值。如果类型为CONSTANT,存放的是常量的值;如果类型为VARIABLE或PROCEDURE,存放所属分程序的层次,主程序的层次为0;在主程序中定义的内容层次为1;主程序内第一层分程序中定义的内容层次为2,以此类推。
- ADR,地址。如果为简单变量或常量,则记录的是该量在数据区所占单元的相对地址,用DX表示给本层局部变量分配的相对存储位置,每说明一个变量后DX加1;如果为过程,则存放该过程的分程序入口地址(需要返填)
- SIZE,大小。该过程内局部变量的个数,再加上过程活动记录的头3个单元(DL,SL,RA)(需要返填)
例如下面的程序:
const a = 35, b = 49;
var c, d, e;
procedure p;
var g;
对应的符号表为:
| NAME | KIND | VAL/LEVEL | ADD | SIZE |
|---|---|---|---|---|
| a | CONSTANT | 35 | ||
| b | CONSTANT | 49 | ||
| c | VARIABLE | LEV | DX | |
| d | VARIABLE | LEV | DX+1 | |
| e | VARIABLE | LEV | DX+2 | |
| p | PROCEDURE | LEV | p的入口地址 | 4 |
| g | VARIABLE | LEV+1 | DX |
又例如下面的程序:
const a = 25;
var x, y;
procedure p;
var z;
begin
...
end;
procedure r;
var x, s;
procedure t;
var v;
begin
...
end;
begin
...
end;
begin
...
end.
对应的符号表为:
| NAME | KIND | VAL/LEVEL | ADD | SIZE |
|---|---|---|---|---|
| a | CONSTANT | 25 | ||
| x | VARIABLE | LEV | DX | |
| y | VARIABLE | LEV | DX+1 | |
| p | PROCEDURE | LEV | p的入口地址 | 4 |
| z | VARIABLE | LEV+1 | DX | |
| r | PROCEDURE | LEV | r的入口地址 | 5 |
| x | VARIABLE | LEV+1 | DX | |
| s | VARIABLE | LEV+1 | DX+1 | |
| t | PROCEDURE | LEV+1 | t的入口地址 | 4 |
| v | VARIABLE | LEV+2 | DX |
第9章 运行时存储组织
PL/0程序运行栈中的过程活动记录
PL/0程序运行时,每一次过程调用都将在运行栈增加一个过程活动记录。 其中,当前活动记录的起始单元由基址寄存器b指出,结束单元是栈顶寄存器t所指单元的前一个单元。
PL/0的过程活动记录中的头3个单元是固定的联系信息:
- 静态链SL:存放的是定义该过程所对应的上一层过程,最近一次运行时的活动记录的起始单元。
- 动态链DL:存放的是调用该过程前正在运行过程的活动记录的起始单元。过程返回时当前活动记录要被撤销,此时需要动态链信息来修改基址寄存器b的内容。
- 返回地址RA:记录该过程返回后应该执行的下一条指令地址,即调用该过程的指令执行时指令地址寄存器p的内容加1
这样,每当一个过程被调用,就需要在栈上先分配3个空间用来存储上述信息,然后才是分配空间存储过程的局部变量。对于主过程,SL=DL=RA=0。
这里给出一道例题。对于下列程序:
var m, n, g:integer;
function gcd(m,n:integer):integer;
begin
if n = 0 then
g := m
else
g := gcd(n, m mod n)
end;
begin
m := 24;
n := 16;
g := gcd(m, n)
end.
它的运行栈为:
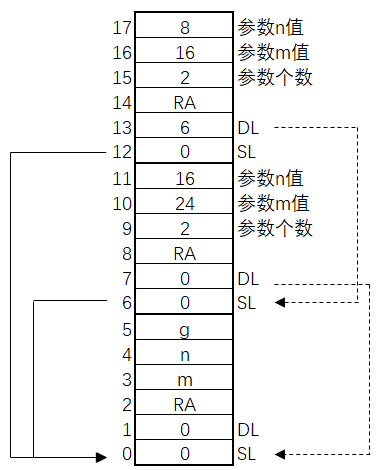
这一章可能要考的内容
- 运行栈的填写(静态链、动态链)
- display表(本质上是记录各个层定义的最新活动记录),建议自己看书
第10章 代码优化
优化技术简介
常用优化技术有:
- 删除多余运算
- 循环不变代码外提
- 强度削弱
- 变换循环控制条件
- 合并已知量
- 复写传播与删除无用赋值
删除多余运算
\((1)T_1:=4*I\\ (2)T_2:=addr(A)-4\\ (3)T_3:=T_2[T_1]\\ (4)T_4:=4*I\\ (5)T_5:=addr(B)-4\\ (6)T_6:=T_5[T_4]\)
可以看到\((4)\)式做了和\((1)\)式重复的工作,可以改写成\(T_4:=T_1\)
循环不变代码外提
原代码:
块1
\((1)P:=0\\
(2)I:=1\)
块2
\((3)T_1:=4*I\\
(4)T_2:=addr(A)-4\\
(5)T_3:=T_2[T_1]\\
(6)P:=P+T_3\\
(7)I:=I+1\\
(8)if \;I<=20\;goto\;(3)\)
可以看到\((4)\)式在每次循环都做重复的工作,可以把它提到循环外来,记得修改跳转:
块1
\((1)P:=0\\
(2)I:=1\\
(3)T_2:=addr(A)-4\)
块2
\((4)T_1:=4*I\\
(5)T_3:=T_2[T_1]\\
(6)P:=P+T_3\\
(7)I:=I+1\\
(8)if \;I<=20\;goto\;(4)\)
强度削弱
把强度大的运算换成强度小的运算,比如用加法换乘法:
块1
\((1)P:=0\\
(2)I:=1\\
(3)T_2:=addr(A)-4\)
块2
\((4)T_1:=4*I\\
(5)T_3:=T_2[T_1]\\
(6)P:=P+T_3\\
(7)I:=I+1\\
(8)if \;I<=20\;goto\;(4)\)
把\((4)\)式经过处理,并修改跳转:
块1
\((1)P:=0\\
(2)I:=1\\
(3)T_1:=0\\
(4)T_2:=addr(A)-4\)
块2
\((5)T_1:=T_1+4\\
(6)T_3:=T_2[T_1]\\
(7)P:=P+T_3\\
(8)I:=I+1\\
(9)if \;I<=20\;goto\;(5)\)
变换循环控制条件
下面的代码中,\(I\)和\(T_1\)保持4倍的线性关系:
块1
\((1)I:=1\\
(2)T_1:=4*I\)
块2
\((3)P:=T_2[T_1]\\
(4)I:=I+1\\
(5)T_1=T_1+4\\
(6)if\;I<=20\;goto\;(3)\)
可以把循环条件\(I<=20\)改为\(T_1<=80\),然后修改\(T_1\)的初始赋值,这样\(I\)在整个循环都没有被用上,可以剔除:
块1
\((1)T_1:=4\)
块2
\((2)P:=T_2[T_1]\\
(3)T_1=T_1+4\\
(4)if\;T_1<=80\;goto\;(2)\)
合并已知量
下面的代码中,在计算\(4*I\)时,\(I\)必定为1:
\((1)I:=1\\
(2)T_1:=4*I\)
因此可以直接在编译期间算出它的值是4:
\((1)I:=1\\
(2)T_1:=4\)
复写传播和删除无用赋值
看下面的代码:
块1
\((1)T_1:=4\\
(2)I:=1\)
块2
\((3)T_2:=T_1\\
...\\
(7)T_3:=T_4[T_2]\\
(8)T_1:=T_1+T_3\\
(9)I:=I+1\\
(10)if\;T_1<=80\;goto\;(3)\)
四元式\((3)\)把\(T_1\)的值写入\(T_2\)中,但\(T_2\)和\(T_1\)的值在\((3)\)到\((7)\)之间没有发生改变,故将\((7)\)改为\(T_3:=T_4[T_1]\)
此时\((3)\)式没有被引用,属于无用赋值,可以删掉。
然后,\((2)\),\((9)\)对\(I\)赋值,但也只是自我引用,其余地方没有需要用到\(I\),属于无用赋值,故可以删掉。
最终变为:
块1
\((1)T_1:=4\)
块2
\(...\\
(5)T_3:=T_4[T_1]
(6)T_1:=T_1+T_3
(7)if\;T_1<=80\;goto\;(2)\)
基本块、流图和循环
基本块
一个基本块内部是顺序执行的,故内部不能有任何停止、分支、跳转。
基本块的划分:
- 条件转移语句或者无条件转移语句和下一句语句之间要划分开
- 跳转的目标语句要和上一句语句之间划分开
例如:
\((1)\quad pi:=3.14\\
(2)\quad ar:=0.0\\
(3)\quad n:=16\\
(4)\quad r:=1\\
(5)\quad if\;n<=1\;goto\;(9)\\
(6)\quad r:=r*n\\
(7)\quad n:=n-1\\
(8)\quad goto\;(5)\\
(9)\quad ar:=2*pi\\
(10)\quad ar:=ar*r\\
(11)\quad print\;ar\)
经过划分后:
B1
\((1)\quad pi:=3.14\\
(2)\quad ar:=0.0\\
(3)\quad n:=16\\
(4)\quad r:=1\)
/////////////////////////////////////////////////
B2
\((5)\quad if\;n<=1\;goto\;(9)\)
/////////////////////////////////////////////////
B3
\((6)\quad r:=r*n\\
(7)\quad n:=n-1\\
(8)\quad goto\;(5)\)
/////////////////////////////////////////////////
B4
\((9)\quad ar:=2*pi\\
(10)\quad ar:=ar*r\\
(11)\quad print\;ar\)
流图
流图 是在已经划分基本块的基础上,构造一个有向图。
- 两个相邻基本块如果上面的没有跳转,可以直接和下面的相连
- 如果当前基本块最后存在无条件跳转,直接和跳转的目标基本块相连
- 如果当前基本块存在最后有条件跳转,需要先和下面相邻的基本块相连,然后和跳转的目标基本块相连
上面的基本块集合为\(\{B1,B2,B3,B4\}\),可以用有向边集合\(\{B1\rightarrow B2, B2\rightarrow B3, B3\rightarrow B2, B2\rightarrow B4\}\),这里不画图。
循环
支配结点,指的是对任意两个结点m和n来说,如果从流图的首结点出发,到达n的任一通路都要经过m,则称m是n的支配结点,记为\(m\;DOM\;n\)
下图是某个程序的流图,其结点即程序中的基本块

所有结点的支配结点集D(n):
\(D(1)=\{1\}\\
D(2)=\{1,2\}\\
D(3)=\{1,2,3\}\\
D(4)=\{1,2,4\}\\
D(5)=\{1,2,4,5\}\\
D(6)=\{1,2,4,6\}\\
D(7)=\{1,2,4,7\}\)
该图的有向边集合为:\(\{1\rightarrow 2, 2\rightarrow 3, 2\rightarrow 4, 3\rightarrow 4, 4\rightarrow 2, 4\rightarrow 5, 4\rightarrow 6, 5\rightarrow 7, 6\rightarrow 6, 6\rightarrow 7, 7\rightarrow 4\}\)
回边指的是存在一条边\(A\rightarrow B\),使得\(B\in D(A)\)。故上图的回边有\(4\rightarrow 2, 6\rightarrow 6,7\rightarrow4\)
一个循环由其中的一条回边\(A\rightarrow B\)对应的两个结点\(B,A\),以及有通路到达\(A\)而不经过\(B\)的所有结点组成,并且保证\(B\)是该循环的唯一入口结点。
如包含回边\((6\rightarrow 6)\)的循环为\(\{6\}\)
包含回边\((7\rightarrow 4)\)的循环为\(\{4,5,6,7\}\)
包含回边\((4\rightarrow 2)\)的循环为\(\{2,3,4,5,6,7\}\)
这一章可能的考点
- 划分基本表、画出流图、求支配集、找回边、找循环
- 代码局部优化
PL/0编译程序
因为居然还有编程填空题这种恐怖存在,需要了解下面这些内容,不然填空都不知道怎么填。
可以用的全局变量如下:
| 全局变量 | 含义 |
|---|---|
| sym | 当前读取到的符号类型 |
| num | 当前读取到的值 |
| id | 当前读取到的标识符名称 |
| cx | 当前中间代码将被写入时的索引 |
| tx | 当前符号表将被写入的索引 |
| code | 指令数组,类型为instruction |
在分析控制流的函数可以用的变量如下:
| 变量 | 含义 |
|---|---|
| cx1,cx2 | 分别记录条件为真/假时需要跳转的地址 |
instruction的结构体如下:
typedef struct
{
int f; // 函数类别
int l; // 层级
int a; // 地址/立即数/操作类别
} instruction;
函数类别和操作类别如下:
enum opcode
{
LIT, // 取立即数
OPR, // 操作
LOD, // 读取
STO, // 保存
CAL, // 调用
INT, // 初始化空间
JMP, // 无条件跳转
JPC // 有条件跳转
};
enum oprcode
{
OPR_RET, OPR_NEG, OPR_ADD, OPR_MIN,
OPR_MUL, OPR_DIV, OPR_ODD, OPR_EQU,
OPR_NEQ, OPR_LES, OPR_LEQ, OPR_GTR,
OPR_GEQ
};
符号类别如下:
enum symtype
{
NUMBER,
// 符号类型
PLUS,
MINUS,
TIMES,
SLASH,
ODD,
EQU, // =
NEQ, // <>
LES, // <
LEQ, // <=
GTR, // >
GEQ, // >=
LPAREN, // (
RPAREN, // )
COMMA, // ,
SEMICOLON, // ;
PERIOD, // .
// 关键字
BEGINSYM,
ENDSYM,
IFSYM,
THENSYM,
WHILESYM,
DOSYM,
CALLSYM,
CONSTSYM,
VARSYM,
PROCEDURESYM
}
可以用的全局函数如下:
| 全局函数 | 含义 |
|---|---|
| getsym | 获取下一个符号的类型到sym。如果sym是number,则num将会存放值;如果sym是标识符,id将存放标识符名称 |
| gen | 生成下一条指令,cx加1 |
处理while循环的题目
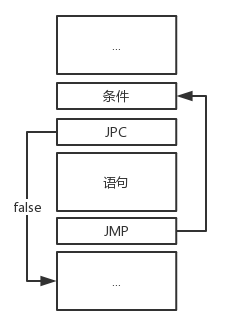
<while语句> ::= <while><条件><do><语句>
case WHILESYM:
__________; // 第一个空为cx1 = cx,记录JMP要跳转的位置
getsym();
condition(SymSetAdd(DOSYM, FSYS), LEV, TX);
__________; // 第二个空为cx2 = cx,记录JPC指令的位置
gen(JPC, 0, 0);
if (__________) // 第三个空为sym == DOSYM,处理到do
getsym();
else
error(18);
statement(fsys, lev, tx);
gen(__________); // 第四个空为jmp, 0, cx1,要知道跳转回开始判断条件的地方
__________; // 第五个空为code[cx2].a = cx,回填JPC指令的跳转位置
break;
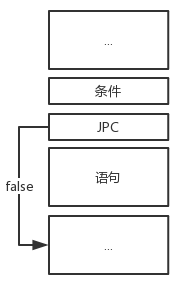
处理if或if-else条件语句的题目
if条件语句图
if-else条件语句图
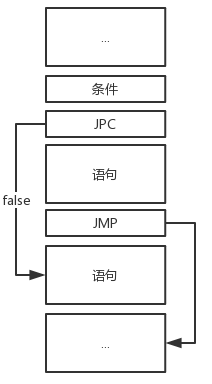
<条件语句> ::= <if><条件><then><语句>[<else><语句>]
下题处理了if条件语句和if-else条件语句的情况:
case IFSYM:
getsym();
condition(SymSetUnion(SymSetNew(THENSYM, DOSYM), FSYS), LEV, TX);
if (SYM == THENSYM)
getsym();
else
error(16);
________; // 第一个空为cx1 = cx;,记录JPC位置待回填
gen(JPC, 0, 0);
statement(SymSetUnion(SymSetNew(ELSESYM), FSYS), LEV, TX);
if (__________) // 第二个空为SYM != ELSESYM,此时在分析else符号
code[cx1].a = cx;
else
{
getsym();
cx2 = cx;
gen(JMP, 0, 0);
__________; // 第三个空为code[cx1].a = cx,此时在分析false部分的语句开头,回填JPC的地址
statement(FSYS, LEV, TX);
__________; // 第四个空为code[cx2].a = cx,此时为执行完true部分语句后的JMP回填跳转地址
}
break;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号