编译原理--01 文法和语言、词法分析复习(清华大学出版社第3版)

前言

这篇博客系列是我为了应付期末编译原理的考试顺便做的复习总结，不适合用于直接学习，而是用于快速过一遍考点。不过现在考试已经结束了，做了不到半个钟就做完卷子了。到头来考的深度也只有里面的一半左右= =不过至少是考点全覆盖了23333

最后考了95分嘿嘿，甚至还有考100的

目录

01 文法和语言、词法分析复习

02 自顶向下、自底向上的LR分析复习

03 语法制导翻译和中间代码生成复习

04 符号表、运行时存储组织和代码优化复习

05 用C++手撕PL/0

第2章 文法和语言

符号和符号串

空符号串用\(\varepsilon\)表示，长度为0

若 \(\Sigma=\{0,1\}\) ，则 \(\Sigma^*=\{\varepsilon,0,1,00,11,000,001,...\}\)，称 \(\Sigma^*\) 为集合 \(\Sigma\) 的闭包；\(\Sigma^+=\{0,1,00,11,000,001,...\}\)，称\(\Sigma^+\)为集合\(\Sigma^+\)的正闭包。

文法和语言的形式定义

规则或产生式或生成式，表示为 \(\alpha\rightarrow\beta\) 或 \(\alpha::=\beta\)

文法 \(G\) 定义为四元组 \((V_N, V_T, P, S)\)
\(V_N\)为非终结符集合
\(V_T\)为终结符集合
\(P\)为规则集
\(S\)为识别符或开始符

例如：
\(G[S]:S\rightarrow0S1\)
\(S\rightarrow01\)

直接推导用 \(\Rightarrow\)，如 \(0S1\Rightarrow 00S11\)
长度为\(n(n\geq1)\)的推导用 \(\stackrel{+}{\Rightarrow}\)，如\(S\stackrel{+}{\Rightarrow} 000S111\)
长度为\(n(n\geq0)\)的推导用 \(\stackrel{*}{\Rightarrow}\)，如\(S\stackrel{*}{\Rightarrow} 000S111 \stackrel{*}{\Rightarrow} 000S111\)

句型：对\(S\stackrel{*}{\Rightarrow}x\)，称x是文法G[S]的句型。x可以包含非终结符
句子：若上述x仅由终结符构成，则x是文法G[S]的句子

文法描述的语言 是 该文法一切句子的集合，如：
\(L(G[S])=\{0^n1^n|n\geq1\}\)

文法类型

文法类型	每个产生式\(\alpha\rightarrow\beta\)的特点
0型文法	\(\alpha\in(V_N\cup V_T)^*\)且至少含一个非终结符，且\(\beta\in(V_N\cup V_T)^*\)
1型 或 上下文有关文法	在0型文法的基础上，还满足\(\mid\beta\mid\geq\mid\alpha\mid\)，仅\(S\rightarrow\varepsilon\)除外
2型 或 上下文无关文法	\(\alpha\)是一个非终结符，\(\beta\in(V_N\cup V_T)^*\)
3型 或 正规文法	满足\(A\rightarrow aB\)或\(A\rightarrow a\)（右线性文法）的形式，即\(\beta\)中只有1个非终结符，以及0或1个终结符。左线性文法为\(A\rightarrow Ba\)或\(A\rightarrow a\)型

最左推导：在推导\(\alpha\Rightarrow\beta\)中，对\(\alpha\)中最左非终结符进行替换
最右推导：又称作规范推导，所推导得到的句型称为右句型，或规范句型

二义性：一个文法存在某个句子对应两棵不同的语法树

语法树

已知文法\(G[S]:\)
\(S\rightarrow aAS\)
\(A\rightarrow SbA\)
\(S\rightarrow a\)
\(A\rightarrow ba\)

文法G的句型aabbaa的一颗推导树为：

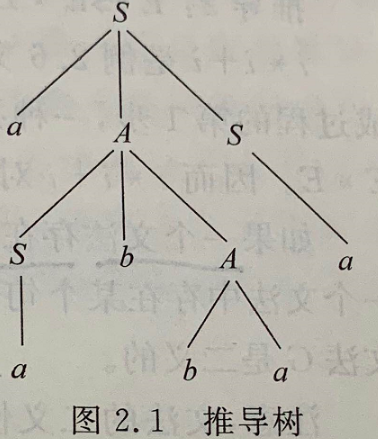
短语：若\(S\stackrel{*}{\Rightarrow}\alpha A\delta\) 且\(A\stackrel{+}{\Rightarrow}\beta\)，则称 \(\beta\) 为句型 \(\alpha A\delta\) 相对于非终结符\(A\)的短语
直接短语：特别的，若\(A\Rightarrow \beta\)，则称 \(\beta\) 为句型 \(\alpha A\delta\) 相对于规则\(A\rightarrow \beta\)的直接短语
句柄：规范句型(右句型)的直接短语。对于无二义文法，一个右句型的唯一句柄是其所有直接短语中最左边的那一个

短语即找出所有非终结符为根节点构成的子树的叶子节点，故有\(a, ba, abba, aabbaa\)

直接短语即找出所有非终结符为根节点构成的只有两层高度子树的叶子节点，故有\(a, ba\)

句柄要求使用最右推导，对上面的推导树来看有\(S\Rightarrow aAS\Rightarrow aAa\Rightarrow aSbAa\Rightarrow aSbbaa\Rightarrow aabbaa\)，我们需要看的是最后一次推导，这里使用的是\(S\rightarrow a\)，因此其句柄为：\(a\)。

可见，短语、直接短语、句柄的存在要求语法树至少含有2级的叶结点（或3层高度）。

文法限制

有害规则：如\(U\rightarrow U\)，只会引发二义性
多余规则：非终结符D不在任何规则的右部出现，即不可到达的

这一章的可能考点

1. 已知文法求语言
2. 已知语言求文法
3. 列出句型的短语、直接短语、句柄
4. 语法树、最左推导、规范推导

第3章 词法分析

正规式

----正规式----	含义
\(a\)	仅a
\(a\mid b\)	该字符可以为a或b
\(ab\)	字符a后面紧跟b
\(a^*\)	n(n>=0)个连续的a
\((a\mid b)b\)	ab或bb

正规文法与正规式的等价性

正规式转化为正规文法

对\(A\rightarrow x^*y\)型正规产生式，重写为：
\(A\rightarrow xB\)
\(A\rightarrow y\)
\(B\rightarrow xB\)
\(B\rightarrow y\)

对\(A\rightarrow x\mid y\)型正规产生式，重写为：
\(A\rightarrow x\)
\(A\rightarrow y\)

正规文法转化为正规式

	文法产生式	----正规式----
规则1	\(A\rightarrow xB\) 和 \(B\rightarrow y\)	\(A=xy\)
规则2	\(A\rightarrow xA\mid y\)	\(A=x^*y\)
规则3	\(A\rightarrow x\) 和 \(A\rightarrow y\)	\(A=x\mid y\)

有穷自动机

确定的有穷自动机(DFA)

确定的有穷自动机\(M\)是一个五元组：\(M=(K,\Sigma,f,S,Z)\)
\(K\)是一个有穷状态集
\(\Sigma\)是一个输入符号表
\(f\)是状态转换函数，例如\(f(k_i,a)=k_j (k_i,k_j\in K)\)
\(S\in K\)，是唯一的一个初态
\(Z\subseteq K\)，是一个终态集

DFA的确定性表现在转换函数 \(f:K\times\Sigma\rightarrow K\) 是一个单值函数

例如： DFA \(M=(\{S,U,V\}, \{a,b\}, f, S, \{V\})\)
\(f(S,a)=U\)
\(f(S,b)=V\)
\(f(U,b)=V\)
\(f(V,a)=U\)

现验证\(bab\)是否为\(M\)所接受，因为：
\(f(S, bab)=f(f(S,b), ab)=f(V,ab)=f(f(V,a),b)=f(U,b)=V\)，而\(V\)属于终态，故\(bab\)可为\(M\)接受。

不确定的有穷自动机(NFA)

不确定的有穷自动机\(M\)是一个五元组：\(M=(K,\Sigma,f,S,Z)\)
\(K\)是一个有穷状态集
\(\Sigma\)是一个输入符号表
\(f\)是\(K\times\Sigma^*\rightarrow 2^K\)的多值映像，即允许函数值有多种结果
\(S\in K\)，是非空初态集
\(Z\subseteq K\)，是一个终态集

NFA可以使用空转移，但DFA不可以。例如：\(f(0, \varepsilon)=\{0,3\}\)

NFA转换为等价DFA

状态集合\(I\)的\(\varepsilon-\)闭包，表示为\(\varepsilon-closure(I)\)，是状态集\(I\)中的任何状态\(S\)经过任意条\(\varepsilon\)弧能到达的状态的集合。显然，状态集合\(I\)的任何状态\(S\)都属于\(\varepsilon-closure(I)\)

状态集合\(I\)的\(a\)弧转换，表示为\(move(I,a)\)，定义为状态集合J，其中J是所有那些可以从\(I\)中某一状态经过一条\(a\)弧而到达的状态全体

子集法

----------初始状态集----------	\(\varepsilon-closure(I)\)	----a----	----b----
\(\{0\}\)	\(\{0,1,2,4,7\}\)
\(T_0=\{0,1,2,4,7\}\)		\(\{3,8\}\)	\(\{5\}\)
\(\{3,8\}\)	\(\{1,2,3,4,6,7,8\}\)
\(\{5\}\)	\(\{1,2,4,5,6,7\}\)
\(T_1=\{1,2,3,4,6,7,8\}\)		\(\{3,8\}\)	\(\{5,9\}\)
\(T_2=\{1,2,4,5,6,7\}\)		\(\{3,8\}\)	\(\{5\}\)
\(\{5,9\}\)	\(\{1,2,4,5,6,7,9\}\)
\(T_3=\{1,2,4,5,6,7,9\}\)		\(\{3,8\}\)	\(\{5,10\}\)
\(\{5,10\}\)	\(\{1,2,4,5,6,7,10\}\)
\(T_4=\{1,2,4,5,6,7,10\}\)		\(\{3,8\}\)	\(\{5\}\)

重命名状态集	a	b
\(T_0\)	\(T_1\)	\(T_2\)
\(T_1\)	\(T_1\)	\(T_3\)
\(T_2\)	\(T_1\)	\(T_2\)
\(T_3\)	\(T_1\)	\(T_4\)
\(T_4\)	\(T_1\)	\(T_2\)

DFA的最小化

1. 将\(P\)划分为终态集与非终态集，得\(P'=\{N,T\}\)
2. 递归地分割\(P'\)中的子集，使得被分割的子集中的所有状态都能够根据不同的输入符号转换到被分割的目标子集中的所有状态
3. 直到不可再被分割后，将\(P'\)中的每个子集合并为一个状态。含原初态的状态为初态，而含原终态的状态为终态。

\(P=\{1,2,3,4,5,6,7\}\)被划分为\(P_0=\{\{1,2,3,4\},\{5,6,7\}\}\)

在非终态集中，在1和2构成集合时，通过a可以到达终态集，通过b可以到达3。而3,4通过b到达的是终态集，显然有区别，故划分为\(P_1=\{\{1,2\},\{3,4\},\{5,6,7\}\}\)

在6和7构成集合时，通过a可以到达4，通过b可以到达集合{1,2}，而5通过a到达的是7，显然有区别，故划分为\(P_2=\{\{1,2\},\{3,4\},\{5\},\{6,7\}\}\)

由于3通过a到达集合{1,2}，而4通过a到达4，有明显区分，故划分为\(P_3=\{\{1,2\},\{3\},\{4\},\{5\},\{6,7\}\}\)

最后不能再划分了，因此令1代表{1,2}，消去2，令6代表{6,7}，消去7.最终得到的为最小化的DFA \(M'\)

正规式和有穷自动机的等价性

略

正规文法和有穷自动机的等价性

略

这一章的可能考点

1. 根据文法构造DFA，或给定NFA转DFA
2. DFA的最小化
3. 正规文法、正规式、有穷自动机之间的转换