LeetCode刷题笔记9.9-9.15

LeetCode刷题笔记9.9-9.15

二叉树

主要学两种遍历方式：层序遍历、递归遍历

1)层序遍历BFS

基本思想：逐层遍历元素，可以借助队列，先进先出，队首出元素的同时进该元素的左右节点（这也是最简单的实现方式）

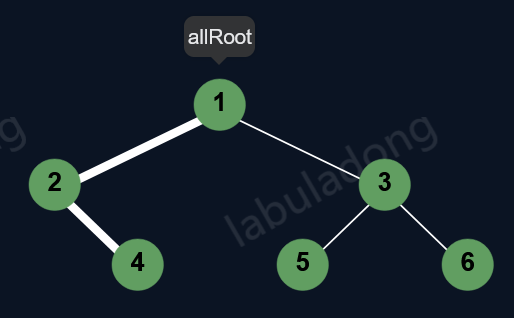
队列Q：1 -> 出1 进2,3（2，3）-> 出2 进4（3，4）-> 出3 进5,6（4，5，6）-> 出4（5，6）-> 出5（6）-> 出6（空）
队列进出元素的操作在遇到队列为空时停止

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while (!q.isEmpty()) {
        TreeNode cur = q.poll();
        // 访问 cur 节点
        System.out.println(cur.val);

        // 把 cur 的左右子节点加入队列
        if (cur.left != null) {
            q.offer(cur.left);
        }
        if (cur.right != null) {
            q.offer(cur.right);
        }
    }
}

进阶思想：在层次遍历过程中记录树的深度
记录深度的时机：

队列Q：1 -> 出1 进2,3（2，3）-> 出2 进4（3，4）-> 出3 进5,6（4，5，6）-> 出4（5，6）-> 出5（6）-> 出6（空）

当前层的所有节点的孩子节点全部列入队列时，此时一定是当前层的最后一个节点刚出队列，比如以上变换过程中的出3后，当前第2层（从1层算起）遍历结束，第3层开始遍历
修改基础的遍历代码：

void levelOrderTraverse(TreeNode root) {
    if (root == null) {
        return;
    }
    int depth = 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while (!q.isEmpty()) {

        int depthSize = q.size();
        for(int i = 0; i < depthSize; i++){
            TreeNode cur = q.poll();
            // 访问 cur 节点
            System.out.println(cur.val);

            // 把 cur 的左右子节点加入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }

        depth++;
    }
}

【二叉树的层序遍历可以用到求与二叉树最短深度/到叶子节点的最短路径相关的题目中，深度遍历必须要遍历完所有树枝的深度，作比较后才可得到】

2)递归遍历DFS

理解递归遍历与迭代循环遍历的区别和联系

// 迭代遍历数组
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {

    }
}

// 递归遍历数组
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // 前序遍历要做的操作
    // 这里是每层递归刚进来的位置 适用于正序遍历
    traverse(arr, i + 1);
    // 后序遍历要做的操作
    // 这里是每层递归快要结束的位置 适用于反序遍历
}

// 迭代遍历单链表
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {

    }
}

// 递归遍历单链表
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

再来看二叉树/多叉树的递归遍历

void traverse(TreeNode root){
    if(root == null) return;
    // 这里是每层递归刚刚进入的位置，是前序的操作
    traverse(root.lchild);
    // 这里是递归左子树结束的位置，是中序的操作
    traverse(root.rchild);    
    // 这里是每层递归将要结束的位置，是后序的操作
}

class Node{
    int val;
    List<Node> children;
}
void traverse(Node root) {
    if (root == null) {
        return;
    }
    // 前序位置
    for (Node child : root.children) {
        // 依次遍历所有孩子节点来递归
        traverse(child);
    }
    // 后序位置
}

由此推导出二叉树的遍历实现规律：
前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点
不仅仅是三个顺序不同的 List：
前序位置的代码在刚刚进入当前二叉树节点的时候执行；
后序位置的代码在将要离开一个二叉树节点的时候执行；
中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。