多项式学习笔记
多项式学习笔记
本文为作者的学习笔记,其中主要包含作者学习时的一些笔记,以及一些例题。如果有小伙伴看到这篇博客没有写完的话,那一定是我咕咕咕了。
FFT
FFT 的中文名称为快速傅里叶变换,英文全称为 Fast Fourier Transform。
系数表示法
我们知道,每一个多项式都有唯一的一组系数,每一组系数也对应着唯一的一个多项式,所以我们可以用一组系数来表示一个多项式:
点值表示法
我们可以把这个多项式看作平面直角坐标系上的一个函数,那么我们就可以从上面选 $ n+1 $ 个点,这些点一定可以唯一表示这个多项式。
为什么这么说呢?我们假设这 $ n+1 $ 个点分别是 $ (x_0,y_0),(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n) $。
那么我们可以由此列出方程:
我们将这些 $ x_i $ 和 $ y_i $ 带入方程组中,便得到了一个有 $ n+1 $ 个方程和 $ n+1 $ 个未知数的方程组,我们正好可以解得唯一的一组 $ a $,也就可以表达这个多项式了。
FFT的基本理论
FFT 干的事情就是快速求出两个多项式 $ f(x),g(x) $ 的乘积 $ h(x) $ ,下面我们来看他是怎么做到的。
首先,我们还是把 $ f(x) $ 与 $ g(x) $ 由系数表示法变为点值表示法,这个过程被叫为 DFT。
假设函数 $ f(x) $ 对应的点坐标分别为 $ (x_i,y_{0,i}) $,函数 $ g(x) $ 对应的点坐标分别为 $ (x_i,y_{1,i}) $。(没错,他们的横坐标要相等)
那么我们就可以得到 $ h(x)={(x_0,y_{0,0}y_{1,0}),(x_1,y_{0,1}y_{1,1}),(x_2,y_{0,2}y_{1,2}),\cdots,(x_n,y_{0,n}y_{1,n})} $。
这里可能有点问题,可能会有人不理解为什么 $ f(x) $ 和 $ g(x) $ 对应纵坐标相乘就是 $ h(x) $ 的纵坐标。
下面我们来证明。
我也不知道为什么有人不理解,总之我当时就很不理解。
因为 $ f(x) $ 对应的点就是 $ (x,f(x)) $ ,$ g $ 和 $ h $ 同理。
所以纵坐标的值实际上就是函数的值。
$ \because f(x)\times g(x)=h(x) $
$ \therefore $ 将 $ f(x) $ 与 $ g(x) $ 的纵坐标相乘便得到了 $ h(x) $ 的横坐标。
那么现在我们知道了 $ h(x) $ 的点值表示法,现在我们就可以将他表示为系数表示法,这个过程被叫为 IDFT。
FFT 的理论就是这个样子,但是我们也知道 DFT 暴力的时间复杂度为 $ O(n^2) $,IDFT 采用高斯消元的做法时间复杂度也为 $ O(n^3) $。显然,FFT 的效率还不如暴力高。那么我们的主要问题就为优化 FFT 了。
当然,上述做法有一些漏洞。假如 $ f(x) $ 与 $ g(x) $ 的最高次项系数都为 $ n $,那么 $ h(x) $ 的最高次项系数就是 $ 2n $。此时肯定是无法用 $ n+1 $ 个点表达 $ h(x) $ 这个多项式了,所以实际上我们要多算一些点。
坐标的取值
我们会发现无论如何,似乎 FFT 的时间复杂度都无法得到有效的优化,那么如果我们取的横坐标是一些特殊的值呢?
复数
设方程 $ x^n=1 $ 在复数意义下的解是 $ n $ 次复根,那么这样的解显然会有 $ n $ 个。设 $ \omega_n=e^\frac{2\pi i}{n} $,那么 $ x^n=1 $ 这个方程的解为 $ \omega_n^k{k|0,1,\cdots,n-1} $。
另一方面我们可以根据欧拉公式,也可以得到 $ \omega_n=e^\frac{2\pi i}{n}=\cos\left(\dfrac{2\pi}{n}\right)+i\times \sin\left(\dfrac{2\pi}{n}\right) $。
放一张 oi-wiki 上的图片,有助于理解。
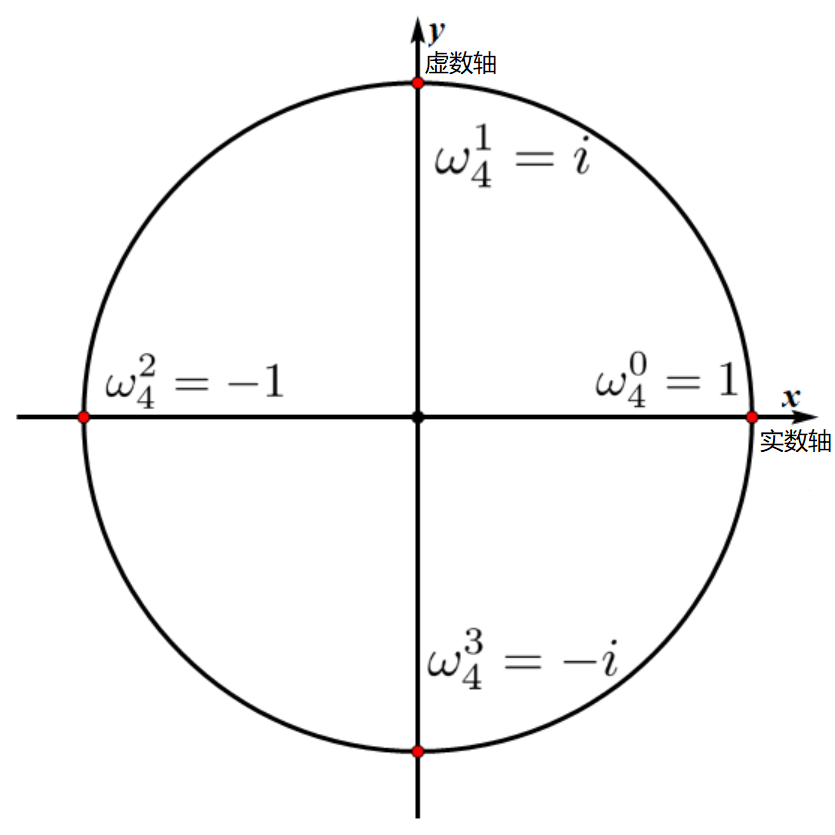
复数的性质
对于任意的正整数 $ n $ 及整数 $ k $。
三个公式放到上面那张图里面都不难理解。
复数的运算
设 $ x=ai+b,y=ci+d $,下面我们来推导复数的计算。
复数的除法也是可以推导的,不过我们暂时用不到。
我们可以打出一份复数的结构体。
struct fs//因为英语不好,所以就用拼音了......
{
double x,y;//x为实部,y为虚部,也就是说这个复数为x+yi
fs(double xx=0,double yy=0){ x=xx,y=yy;}
fs operator + (fs b){ return fs(x+b.x,y+b.y);}
fs operator - (fs b){ return fs(x-b.x,y-b.y);}
fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
DFT
首先我们要将一个函数由系数表示法变为点值表示法,我们设这个函数为 $ f(x) $,且第 $ i $ 项的系数为 $ a_i $。
为了方便起见,我们设 $ f(x) $ 的项数 $ n $ 为 $ 2 $ 的整数次幂,如果项数不够可以补齐。
首先我们设:
那么就会有 $ f(x)=g(x ^2)+xh(x ^2) $。
我们现在要得到 $ n $ 个点的坐标,他们的横坐标分别为 $ \omega _n ^0,\omega _n ^1,\cdots,\omega _n ^{n-1} $,下面我们来推式子(颓柿子)。
可以发现什么?$ f(\omega_n^k) $ 与 $ f\left(\omega_n^{k+\frac{n}{2}}\right) $ 经过化简后第一项相同,第二项互为相反数。这时我们是否可以快速进行 DFT 呢?
设对一个项数为 $ n $ 的多项式进行 DFT 的过程时间复杂度为 $ T(n)=2T\left(\dfrac{n}{2}\right)+O(n) $。
分析可得时间复杂度为 $ T(n)=O(n\log n) $。
那么我们就可以把 DFT 的代码打出来。
//这里前面还需要复数的结构体,但是前面已经打过了,不再重复
const double PI=acos(-1);//这个函数可以得到精确的圆周率
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
void DFT(fs *a,int n)
{
if(n==1) return ;
vector<fs>mem(n);//开一个数组记录之前的值
for(int i=0;i<n;i++) mem[i]=a[i];
for(int i=0;i<n/2;i++) a[i]=mem[2*i];
for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
//将一个函数f进行分治,a的前半部分为g,后半部分为h
DFT(a,n/2),DFT(a+n/2,n/2);//进行分治
fs now(1,0),step=omega(n);
for(int i=0;i<n/2;i++)
{
//根据公式计算a[i]与a[i+n/2]
//注意这里顺序不能错,一定要先计算a[i+n/2]
fs num=a[i+n/2];
a[i+n/2]=a[i]-now*num;
a[i]=a[i]+now*num;
now=now*step;
}
}
这个代码还可以进行一些常数优化,不过我们后面一起进行优化。
IDFT
这个时候我们得到了答案多项式的点值表示法,我们设这个函数的第 $ i $ 项的系数为 $ a _i $ ,$ n $ 个点的坐标分别为 $ (\omega _n ^i,y _i) $ 。
首先我们可以换一个方式表示这些点与系数的关系。
我们把这些式子写成矩阵的形式。
我们再来看一看最左边的这个矩阵有什么性质:
右边的那个矩阵恰好是单位矩阵的 $ n $ 倍,那么我们就可以把最上面的那个矩阵进行转化。
我们有什么好方法?照样采用 DFT 的方法,对函数按照奇偶进行计算。
首先我们知道 $ \dfrac{1}{\omega _n ^{i}}=\omega _n ^{-i} $,那么我们再对上面的式子进行转化。
令 $ f(\omega _n ^{-i})=na _i=\sum\limits _{j=0} ^{n-1}\omega _n ^{-ij}y _j $
还是像上面一样,我们设:
那么就有:
我们又可以发现什么?$ f(\omega_n^{-k}) $ 与 $ f\left(\omega_n^{-k-\frac{n}{2}}\right) $ 经过化简后第一项相同,第二项互为相反数。这时我们是否可以快速进行 IDFT 呢?
设对一个项数为 $ n $ 的多项式进行 IDFT 的过程时间复杂度为 $ T(n)=2T\left(\dfrac{n}{2}\right)+O(n) $。
分析可得时间复杂度为 $ T(n)=O(n\log n) $。
那么我们就可以把 IDFT 的代码打出来。
//这里前面还需要复数的结构体,但是前面已经打过了,不再重复
const double PI=acos(-1);//这个函数可以得到精确的圆周率
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
void IDFT(fs *a,int n)
{
if(n==1) return ;
vector<fs>mem(n);//开一个数组记录之前的值
for(int i=0;i<n;i++) mem[i]=a[i];
for(int i=0;i<n/2;i++) a[i]=mem[2*i];
for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
//将一个函数f进行分治,a的前半部分为g,后半部分为h
IDFT(a,n/2),IDFT(a+n/2,n/2);//进行分治
fs now(1,0),step=omega(n);
step.y=-step.y;
for(int i=0;i<n/2;i++)
{
//根据公式计算a[i]与a[i+n/2]
//注意这里顺序不能错,一定要先计算a[i+n/2]
fs num=a[i+n/2];
a[i+n/2]=a[i]-now*num;
a[i]=a[i]+now*num;
now=now*step;
}
}
//别忘了最后要把所有a[i]变为a[i]/n
没错这一整段是从上面那里复制之后改了一下。
FFT的优化
首先解决一个问题:我们在进行 DFT 与 IDFT 时都默认 $ n $ 为一个形如 $ 2^k $ 的数字,但是我们在实际应用中并不会全是这种情况。
其实只需要取一个比这个数大并且的最小的 $ 2^k $ 就可以了。
合二为一
我们可以发现 DFT 与 IDFT 的函数中只有一句不一样,那么我们就可以把这两个函数合二为一。
现在我们已经打得差不多了,我们来提交试一下。
代码:
#include<cstdio>
#include<vector>
#include<cmath>
using namespace std;
const double PI=acos(-1);//这个函数可以得到精确的圆周率
struct fs//因为英语不好,所以就用拼音了......
{
double x,y;//x为实部,y为虚部,也就是说这个复数为x+yi
fs(double xx=0,double yy=0){ x=xx,y=yy;}
fs operator + (fs b){ return fs(x+b.x,y+b.y);}
fs operator - (fs b){ return fs(x-b.x,y-b.y);}
fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs a[5000000];
fs b[5000000];
void DFT(fs *a,int n,bool dft)
{
//当dft为1的时候,进行DFT
//当dft为0的时候,进行IDFT
if(n==1) return ;
vector<fs>mem(n);//开一个数组记录之前的值
for(int i=0;i<n;i++) mem[i]=a[i];
for(int i=0;i<n/2;i++) a[i]=mem[2*i];
for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
//将一个函数f进行分治,a的前半部分为g,后半部分为h
DFT(a,n/2,dft),DFT(a+n/2,n/2,dft);//进行分治
fs now(1,0),step=omega(n);
if(!dft) step.y=-step.y;
for(int i=0;i<n/2;i++)
{
//根据公式计算a[i]与a[i+n/2]
//注意这里顺序不能错,一定要先计算a[i+n/2]
fs num=a[i+n/2];
a[i+n/2]=a[i]-now*num;
a[i]=a[i]+now*num;
now=now*step;
}
}
int n,m;
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
m+=n,n=1;for(;n<=m;n<<=1);
DFT(a,n,1),DFT(b,n,1);
for(int i=0;i<n;i++) a[i]=a[i]*b[i];
DFT(a,n,0);
for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].x/n+0.5));
return 0;
}
蝴蝶变换
虽然这份代码 AC 了,但是它显然还不够快,我们还需要进行亿点点常数优化。
可以注意到一个过程中常数比较大的地方:就是 DFT 过程中数组的打乱。不难发现,这个部分的时间复杂度为 $ O(n\log n) $,而且我们这里还多开了大约 $ 2n $ 个复数(就是那个叫mem的 vector)。
我们来找一下这个地方数字变化的规律,这里以 $ n=8 $ 举例,而且数字的下标以二进制书写,便于发现规律。
我们可以发现什么?
没错,交换前后每个位置上的数字的二进制位全部是相反的。
当然这是我们发现的结论,现在我们来证明。
采用数学归纳法:
首先我们知道当 $ n=1 $ 时,这个结论显然成立,因为这个时候只有一个数字。
现在我们要证明当 $ n=2^k(k>0) $ 时结论成立,我们假设当 $ n=2^{k-1} $ 时结论成立。
设 $ f_{i,j} $ 为第 $ i $ 个位置上的数在 $ n=2^j $ 时经过交换之后到的地方,一个数字 $ i $ 二进制下的最低位为 $ a_i $。
那么 $ f_{i,k}=a_i\times 2^{k-1}+f_ {i \mod 2^{k-1} ,k-1} $ 。
显然,$ i $ 的最后一位放到了最前面,前面的 $ k-1 $ 位经过翻转后放到了后面,这个结论显然是正确的。
现在要做的就是快速计算这个翻转后的值,显然也是可以快速进行计算的。
//wh[i]表示i这个数经过翻转以后所对应的值
//wh[0]=0,不进行计算
for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
//当i的最后一位为0时,wh[i]=(wh[i>>1]>>1)
//当i的最后一位为1时,wh[i]=(wh[i>>1]>>1)+(n>>1)
//这个显然是正确的,道理和上面证明的过程差不多。
这部分时间复杂度为 $ O(n) $,这种 FFT 比起之前的常数小了一些。
此外还有一些别的优化,例如提前计算 step 的值,将递归改为循环等,由于比较简单,这里不详细展开。
我们就直接重写代码,看一下提交结果。
代码:
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const double PI=acos(-1);
struct fs
{
double x,y;
fs(double xx=0,double yy=0){ x=xx,y=yy;}
fs operator + (fs b){ return fs(x+b.x,y+b.y);}
fs operator - (fs b){ return fs(x-b.x,y-b.y);}
fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs step[5000001];
int wh[5000001];
fs a[5000000];
fs b[5000000];
int n,m;
void DFT(fs *a,int n,bool dft)
{
for(int i=0;i<n;i++) if(i<wh[i]) swap(a[i],a[wh[i]]);
//有这个if就可以确保只换一次,当然也可以写成if(i>wh[i])...
for(int len=2;len<=n;len<<=1)
{
fs ste=step[len];
if(!dft) ste.y=-ste.y;
for(int l=0;l<n;l+=len)
{
fs now(1,0);
for(int i=l;i<l+len/2;i++)
{
fs num=a[i+len/2]*now;
a[i+len/2]=a[i]-num;
a[i]=a[i]+num;
now=now*ste;
}
}
}
}
void FFT(fs *a,fs *b,int n)
{
for(int i=2;i<=n;i<<=1) step[i]=omega(i);
for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
DFT(a,n,1),DFT(b,n,1);
for(int i=0;i<n;i++) a[i]=a[i]*b[i];
DFT(a,n,0);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
m+=n,n=1;for(;n<=m;n<<=1);
FFT(a,b,n);
for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].x/n+0.5));
return 0;
}
三次变两次
三次变两次是通过一种特殊的方法,少进行一次 DFT 的优化(由原来的 $ 2 $ 次 DFT 和 $ 1 $ IDFT变为各有一次)。
假设我们现在想要求两个多项式 $ f(x) $ 和 $ g(x) $ 的乘积,不妨设复多项式 $ h(x)=f(x)+g(x)i $。
那么就有 $ h ^2(x)=(f(x)+g(x)) ^2=f ^2(x)+g ^2(x)+2f(x)g(x)i $。
它的虚部不就正好是我们要求的乘积的两倍吗?
代码:
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const double PI=acos(-1);
struct fs
{
double x,y;
fs(double xx=0,double yy=0){ x=xx,y=yy;}
fs operator + (fs b){ return fs(x+b.x,y+b.y);}
fs operator - (fs b){ return fs(x-b.x,y-b.y);}
fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs step[5000001];
int wh[5000001];
fs a[5000000];
int n,m;
void DFT(fs *a,int n,bool dft)
{
for(int i=0;i<n;i++) if(i<wh[i]) swap(a[i],a[wh[i]]);
//有这个if就可以确保只换一次,当然也可以写成if(i>wh[i])...
for(int len=2;len<=n;len<<=1)
{
fs ste=step[len];
if(!dft) ste.y=-ste.y;
for(int l=0;l<n;l+=len)
{
fs now(1,0);
for(int i=l;i<l+len/2;i++)
{
fs num=a[i+len/2]*now;
a[i+len/2]=a[i]-num;
a[i]=a[i]+num;
now=now*ste;
}
}
}
}
void FFT(fs *a,int n)
{
for(int i=2;i<=n;i<<=1) step[i]=omega(i);
for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
DFT(a,n,1);
for(int i=0;i<n;i++) a[i]=a[i]*a[i];
DFT(a,n,0);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&a[i].y);
m+=n,n=1;for(;n<=m;n<<=1);
FFT(a,n);
for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].y/n/2+0.5));
return 0;
}
可以看到,快了不少。
NTT
NTT 的中文名称为快速数论变换,英文全称为 Number-theoretic transform,是 FFT 在数论基础上的实现,可以避免FFT的复数运算中的精度损失。
NTT 实际上是将 FFT 中的复数运算巧妙的替换为了整数运算。
原根
若一个正整数 $ g $ 和一个质数 $ p $ 满足对于所有 $ 1\le i<p $ , $ g ^i\pmod p $ 的值互不相同。
NTT原理
实际上,NTT就是选取了适当的模数以及任何一个这个质数的原根,并用一些整数代替了复数(被代替的就是上面的 $ \omega_n^i $)。
直接这样说估计没人懂,举个例子。
就以最常见的 NTT 模数 $ 998244353 $ 和它的原根(之一)$ 3 $ 来举例。
首先一个比较重要的地方,就是 $ 998244352=2^{23} \times 119 $,这是 NTT 模数的关键之一,这个模数减一必须是 $ 2 $ 的较大次幂的倍数。
假设现在要进行 NTT 的多项式共有 $ n $ 项(和 FFT 一样,$ n $ 是 $ 2 $ 的整数次幂),那么用哪个数字代替 $ \omega_n^1 $ 比较合适呢?
不难想到,用 $ 3^\frac{998244352}{n}\pmod{998244353} $ 代替 $ \omega_n^1 $,同理对于其他 $ i $ ,用 $ \left(3 ^\frac{998244352}{n}\right) ^i\pmod{998244353} $ 代替 $ \omega _n ^i$,这样就大功告成。
此外将 FFT 的其他操作(加法,乘法,减法等)改成模意义下的运算,所有的复数都改成整数,就可以了。
同理,假如使用一个质数 $ p $ 与它的原根 $ g $ 进行 NTT 时,使用 $ \left(g ^{\frac{p-1}{n}}\right) ^i\pmod p $ 代替 $ \omega_n^i $ 即可。
正确性证明
不难发现,FFT 能够快速运算的运算在于复数的那三个性质。
同时,这也是 NTT 可以快速计算的关键,因为我们刚刚对于 $ \omega_n^i $ 的取值也满足这些性质!
下面我们来一条一条看。
证明:
注意,对于所有质数 $ p $ 都有 $ g^{p-1}\equiv 1\pmod p $。
证明:
证明:
注意:$ g ^{\frac{p-1}{2}}=\pm\sqrt{g ^{p-1}}=\pm1 $
因为原根的性质,有 $ g^{p-1}=1 $,所以就有 $ g^{\frac{p-1}{2}}\ne 1 $,即 $ g^{\frac{p-1}{2}} $。
NTT 就说完了。
加上快读和快些还能快一点。
下面是几个模板呀。
多项式求逆
设原多项式为 $ f $ ,它的逆为 $ f^{-1} $。
设 $ f_0=f\pmod{x^{\left\lceil\frac{n}{2}\right\rceil}} $ ,它的逆为 $ f^{-1}_0 $。
则一定会有以下几个性质:
则由 $ (3) $ 可得:
两边同时乘上 $ f $ 。(其实只有一边)
也就是说,只要我们知道了 $ f_0^{-1} $ ,就可以在 $ O(n\log n) $ 的时间内把 $ f^{-1} $ 算出来(NTT 把上面的式子卷一下)。
时间复杂度 $ T(n)=T\left(\dfrac{n}{2}\right)+O(n\log n)=O(n\log n) $ 。
任意模数多项式乘法
我们可以发现,这道题里面的模数可能不能满足之前我们对模数的要求,甚至不是一个质数,所以我们不能直接进行 NTT。
这里我使用的是三模数 NTT。
具体做法就是我们找三个可以进行的 NTT 的模数,然后做三遍 NTT,最后使用 CRT 求出答案。
这里我使用的三个模数分别为 $ 998244353=2^{23}\times 119+1,985661441=2^{22}\times 235+1,1004535809=2^{21}\times 479+1 $ 。
直接做就可以了。
然而最后的 CRT 还是有一些细节的,因为个数比较少,所以我们可以手颓柿子:
首先我们知道这些:
所以一定存在三个自然数 $ k_1,k_2,k_3 $ 使得 $ x=k_1p_1+a_1=k_2p_2+a_2=k_3p_3+a_3 $ 。
这样我们就可以求出 $ k_1\bmod p_2 $ 的值了,不妨记作 $ k_1' $ 。
令 $ a_4=k_1'p_1+a_1 $ ,则存在 $ k_4 $ 使得 $ x=k_4p_1p_2+a_4 $ 。
$ a_4 $ 和 $ k_4 $ 都知道了,我们就可以求出 $ x $ 了。
中间的取模还是有很多细节的,具体可以看代码。
把三个数字写成一个结构体,一起 NTT 还能更快亿点,真的是亿点。
分治FFT
虽然写的是FFT,但实际上是分治NTT...
我们要求出一个满足条件的多项式 $ f $ ,但是 $ f $ 的值和 $ f,g $ 有关。
考虑进行分治。
假设我们现在分治到了一个区间 $ [l,r] $ ,下一步肯定是分治 $ [l,mid] $ 这个区间。
然后呢?我们需要快速处理区间 $ [l,mid] $ 向 $ [mid+1,r] $ 的贡献。
实际上 NTT 卷一下就可以了。
时间复杂度 $ T(n)=T\left(\dfrac{n}{2}\right)+O(n\log n)=O(n\log n) $ 。
FMT/FWT
FMT是快速莫比乌斯变换,FWT是快速沃尔什变换。
他们两个是用来解决位运算卷积问题的。
详细点来说,已知两个多项式 $ f,g $ 和一种运算 $ \oplus $ 。
需要快速求 $ h_i=\sum\limits_{j\oplus k=i}f_j\times g_k $ 。
当 $ \oplus $ 为按位与,按位或的时候可以使用 FMT 来解决。
当 $ \oplus $ 为按位异或,按位同或的时候可以使用 FWT 来解决。
当 $ \oplus $ 为加法时就是上面讲过的 FFT/NTT。
先摆出板题:
P4717 【模板】快速莫比乌斯/沃尔什变换 (FMT/FWT)
这道题里面只有与运算,或运算和异或运算,我们一个一个看。
我们令一个多项式 $ a $ 的最高次项的项数 为 $ |a| $ 。
下面的所有描述都假设 $ |f|+1,|g|+1 $ 为 $ 2 $ 的整数次幂,即恰好有 $ 2 $ 的整数次幂项。
一个多项式 $ b $ ,我们使用 $ b_0 $ 表示它的前半部分(次数较小的那一半), $ b_1 $ 表示它的后半部分(次数较大的后一半), $ b[i] $ 表示 $ i $ 次方项的系数。
两个多项式 $ c,d $ ,我们使用 $ c+d $ 表示 $ c $ 和 $ d $ 逐项相加的结果;用 $ (c,d) $ 表示 $ c $ 和 $ d $ 首位相接得到的结果,例如 $ (c_0,c_1)=c $ 。
对于两个自然数 $ i,j $ ,我们用 $ i\in j $ 表示 $ i\And j=i $ ,同时也可以知道 $ i|j=j $ 。
与运算
首先我们定义一个关于多项式的函数 $ FMT(f) $ :
简单来说,就是所有“包含” $ i $ 的位置的和,也就是超集和。
我们的目标就是算出 $ FMT(f),FMT(g) $ ,然后算出 $ FMT(h) $ ,然后算出 $ h $ 。
显然我们就可以在 $ O(|f|^{\log_23}) $ 的时间内求出 $ FMT(f) $ 。
正变换
显然,这样的时间复杂度我们不太可以接受。
所以就会有一个递归公式:
正变换递归公式证明
采用数学归纳法。
当 $ |f|=2^0 $ 时,显然。
假设 $ |f|=2^n $ ,则对于 $ f_0,f_1 $ ,此公式正确。
类比分治的思想,我们将一个区间分成两段,则只需要计算“跨越”中点的贡献,两边进行分治即可。
现在我们想要计算的就是 $ f_1 $ 向 $ f_0 $ 的贡献。(显然 $ f_0 $ 对 $ f_1 $ 没有贡献)
对于一个下标 $ i<2^{n-1} $ ,现在他所缺少的贡献为 $ \sum\limits_{j<2^{n-1}\and i\in j}f_{j+2^{n-1}} $ 。
仔细看这个 $ \sum $ ,看到了什么?
所以这个公式显然是正确的。
至此,我们可以在 $ O(|f|\log |f|) $ 内的时间内求出 $ FMT(f) $ 。
相乘
首先有一个结论:$ FMT(h)=FMT(f)*FMT(g) $ ,这里 $ * $ 为按位乘。 下来我们来证明。
所以说,我们就可直接将 $ FMT(f),FMT(g) $ 乘起来,得到 $ FMT(h) $ 。
逆变换
现在我们知道了 $ FMT(h) $ 的值,想要求出 $ h $ 。
我们定义 $ FMT $ 的逆变换 $ UFMT $ ,使得 $ UFMT(FMT(h))=h $ 。
我们可以从 $ FMT $ 的定义出发,我们知道 $ FMT $ 就是超集和,所以我们只需从大到小,枚举每一个数字的超集即可。
和暴力 $ FMT $ 的时间复杂度是一样的,为 $ O(|f|^{\log_23}) $ 。
显然,万恶的出题人表示无法接受。
所以还是有一个递归公式:
逆变换递归公式证明
还是数学归纳法。
当 $ |f|=2^0 $ 时,显然。
否则,我们假设 $ |f|=2^n $ ,那么公式对于 $ f_0 $ 和 $ f_1 $ 成立。
和正变换一样,只需要计算跨越中点的答案。
我们现在想要知道 $ f_0 $ 需要从 $ f_1 $ 中减去多少。
显然,对于一个下标 $ i<2^{n-1} $ ,它在右边需要减去的值就是 $ f_{i+2^{n-1}} $ 。
也就是说 $ UFMT(f)_0=UFMT(f_0-f_1) $ 。
接下来我们只需要证明对于两个多项式 $ A,B $ ,有 $ UFMT(A)+UFMT(B)=UFMT(A+B) $ 。
根据定义,有:
所以上面的公式都成立。
与变换就是这样的。
或运算
其实这里和与运算差不多,会的小伙伴可以忽略。
我们还是定义一个关于多项式的函数 $ FMT(f) $ :
简单来说,就是所有 $ i $ “包含“的位置的和,也就是子集和。
我们的目标就是算出 $ FMT(f),FMT(g) $ ,然后算出 $ FMT(h) $ ,然后算出 $ h $ 。
显然我们就可以在 $ O(|f|^{\log_23}) $ 的时间内求出 $ FMT(f) $ 。
正变换
显然,这样的时间复杂度我们不太可以接受。
所以就会有一个递归公式:
正变换递归公式证明
采用数学归纳法。
当 $ |f|=2^0 $ 时,显然。
假设 $ |f|=2^n $ ,则对于 $ f_0,f_1 $ ,此公式正确。
类比分治的思想,我们将一个区间分成两段,则只需要计算“跨越”中点的贡献,两边进行分治即可。
现在我们想要计算的就是 $ f_0 $ 向 $ f_1 $ 的贡献。(显然 $ f_1 $ 对 $ f_0 $ 没有贡献)
对于一个下标 $ i\geqslant 2^{n-1} $ ,现在他所缺少的贡献为 $ \sum\limits_{j<2^{n-1}\and j\in i}f_{j} $ 。
仔细看这个 $ \sum $ ,看到了什么?
所以这个公式显然是正确的。
至此,我们可以在 $ O(|f|\log |f|) $ 内的时间内求出 $ FMT(f) $ 。
相乘
首先有一个结论:$ FMT(h)=FMT(f)*FMT(g) $ ,这里 $ * $ 为按位乘。 下来我们来证明。
所以说,我们就可直接将 $ FMT(f),FMT(g) $ 乘起来,得到 $ FMT(h) $ 。
本文来自博客园,作者:Wuyanru,转载请取得作者同意并注明原文链接:https://www.cnblogs.com/Wuyanru/p/dxs.html
本文内容如有侵权行为,请联系作者删除,qq:1395170470


 浙公网安备 33010602011771号
浙公网安备 33010602011771号