[IOI2019]矩形区域

今天打模拟赛遇到的，不得不说有点神仙，所以来写一篇题解。

因为这题是 IOI 的，IOI 的很多题子任务都提示了做法，所以本题解中对大部分 Subtask 进行了分析。

我写这篇题解主要是想要分享一下我做这道题的过程，我认为一道题的思考过程才是最重要的。

注意：

1. 由于作者的叙述习惯不同，本文中所有矩阵的下标均从 $ 1 $ 开始计数。

2. 如果时间复杂度中没有出现 $ m $ ,那么这个地方的时间复杂度默认 $ n,m $ 同阶。

题目链接：luoguP5781

Subtask 5

由于这个 Subtask 条件比较特殊，所以我们先来看它。

这个矩阵最多只有三行，根据题目中对子矩阵的要求，我们可以知道这些子矩阵的元素只能出现在第二行。

首先我们可以知道在这个限制下某个元素可以出现的必要条件是它严格大于它上下的元素。

然后我们将所有第二行的元素从小到大进行排序，并依次加入这些格子，加入某个格子后我们可以查看这个格子所在的连通块是否合法，然后统计答案即可。

干说不明白，不如画几个图。

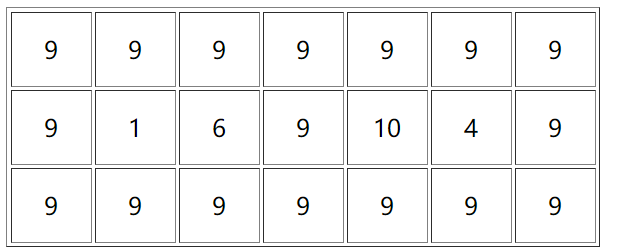
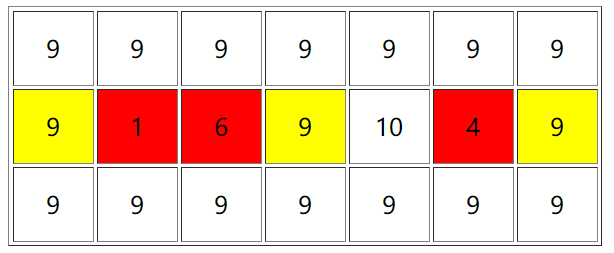
假如这是那个矩阵。

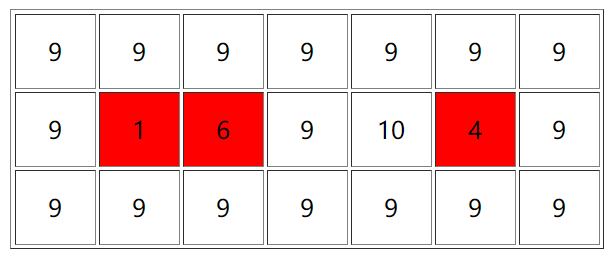
首先我们看一下有哪些格子可能作为子矩阵中的元素，我们将他们标红

然后我们将第二行中的元素排好序，逐个加入。

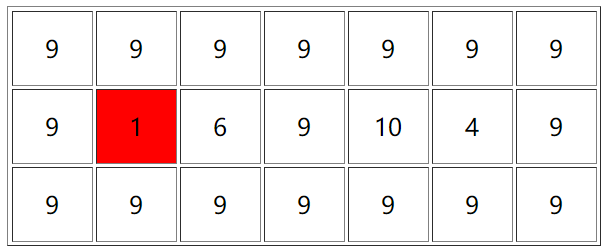
首先我们加入 $ 1 $ ，就可以得到一个子矩阵（左端点下标为 $ 2 $ ，右端点下标也为 $ 2 $ ）。

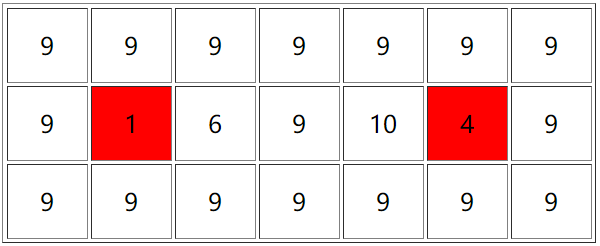
然后我们加入 $ 4 $ ，又可以得到一个子矩阵（左端点下标为 $ 4 $ ，右端点下标也为 $ 4 $ ）。

下来我们加入 $ 6 $ ，又可以得到一个子矩阵（左端点下标为 $ 1 $ ，右端点下标为 $ 6 $ ）。

再然后我们加入 $ 9 $ ，可以发现，新形成的矩阵中没有一个满足要求(没有只包含红色方块)。

最后我们加入 $ 10 $ ，新形成的矩阵还是没有一个满足要求(没有只包含红色方块)。

大概就是这样子的一个过程，我们就可以拿到 $ 10 $ 分的“高”分。

Subtask1

我们可以枚举这个子矩阵的位置，然后对每个子矩阵看一下是否合法。

然后你就会发现这样子是 $ O(n^6) $ 的，虽然这题时限是 $ 5s $ ，可能能过。

我们可以来找一下性质。

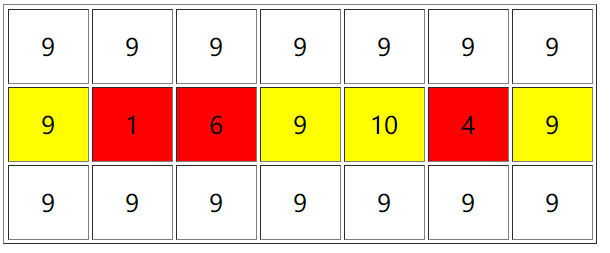
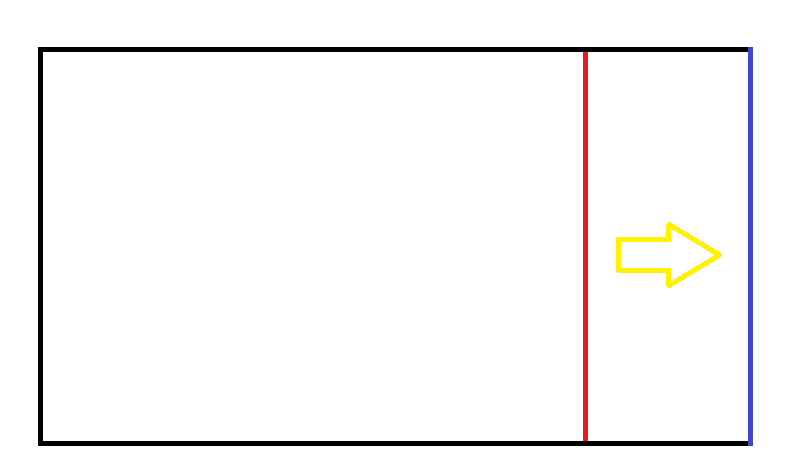
不妨来看一眼，某个子矩阵的右边界从红色的这条线向右走到蓝色的这条线时，这个新矩阵什么情况下是合法的（加入只右移了一格）。

首先我们可以预处理每一行的最大值，这样就可以 $ O(1) $ 算出某一行是否合法，然后我们对于最右边的一列，暴力求出最大值，计算最右边那一列是否合法就可以了。

这样的时间复杂度是 $ O(n^5) $ 的。

这样我们就又可以拿到 $ 8 $ 分。

Subtask2

这个部分做法感觉和 Subtask5 有点类似。

我们可以枚举这个子矩阵的上边界和下边界，这个时候我们看哪一列有可能在这个子矩阵之中出现。（由于我们枚举的是上边界和下边界，所以某一列一定是同时出现或同时不出现。）（出现的条件也差不多，这一列中最大的那个元素比上下的元素都小。）

然后我们就会发现这次我们每一次是加入整个列，那么我们该按什么顺序加入这些列呢？

我们不妨按照这个列的最大值进行排序，最大值越小的越先加入。

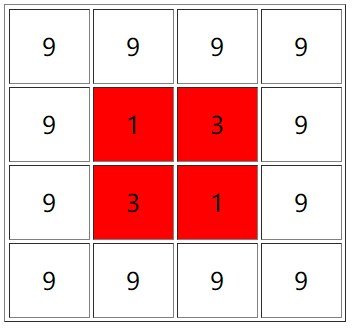
我们再处理一下相邻两列的关系，再来举一个例子。

显然，这两列都是有可能成为某个子矩阵中的元素。

但是，如果第一列在子矩阵中出现，第二列也一定出现；如果第二列出现了，第一列也一定出现，这就形成了一些“连带关系”。

我们只要提前预处理这些“连带关系”，到时候具有连带关系的列一起加入就可以了。

这样子时间复杂度是 $ O(n^4) $ 的，我们又可以拿到 $ 7 $ 分。

Subtask3

注意，这个地方的解法已经和满分有一定关系了（起码我的做法是这个样子）。

不妨这样想，我们要找的子矩阵，既需要满足行的条件，又需要满足列的条件。

那我们能不能找出所有满足行条件的子矩阵，再找出所有满足列条件的子矩阵呢，最后找出它们中相同的呢？

显然，不会算多，也不会算少，这个方法很可行。

我们来看一下所有满足行条件的子矩阵怎么找：

这个问题似乎不太好想，我们从简单的想起，假如说我们要找的子矩阵只有一行，怎么办。

这不就是上面提到的 Subtask5 吗？甚至还简单了亿点。

假如说这个子矩阵有两行呢？它需要满足什么条件？

稍微想一下就会发现，只需要第一行的那些元素可行，第二行的那些元素可行，这个子矩阵就是可行的。

再进一步扩展，如果一个左上角坐标为 $ (u,l) $ ，右下角坐标为 $ (d,r) $ 的子矩阵可行，就只需要第 $ l $ 行到第 $ r $ 中每一行的对应子矩阵（该行的第 $ l $ 列到第 $ r $ 列）可行就可以了。

直接算就可以了，那么时间复杂度是多少呢？

首先我们知道，对于单行来说，可行的子矩阵最多只有 $ m $ 个。

矩阵一共有 $ n $ 行，对于该行的每一个子矩阵，我们都要向下找下面所有行中能和这一行共同组成的子矩阵数量，所以这里时间复杂度是 $ O(n^2m) $ 的。

接下来我们还要进行矩阵的匹配，显然还要使用 set。

最后时间复杂度是 $ O(n^2m\log{nm}) $ 的。

事实上可以过 Subtask1,2,3,5,6。

到这里，我们就可以拿到 $ 50 $ 分，还是挺香的。

Subtask4

我们会发现，这个 Subtask 只需要 $ O(n^3) $ 的时间复杂度就可以了，不难发现，上面那个做法的瓶颈主要在于矩阵的匹配，有什么更好的做法呢？

我们在枚举行矩阵/列矩阵的时候不妨换一种方式，下面拿行矩阵举例。

不难发现，对于一组确认的左边界、上边界与右边界，一个合法的下边界必定是连续的一段区间。

列矩阵也是一样，对于一组确认的上边界、左边界和下边界，一个合法的有边界也是连续的一段区间。

再转化一下，对于一个固定的点，我们把它作为矩阵的左上角，那么一个合法行矩阵的右下角肯定是一堆竖着的线段，一个合法的列矩阵肯定是一堆横着的线段。任何一个横着的线段和任何一个竖着的线段的交点（如果它们有交点）一定是一个合法的右下角。

我们只需要枚举一个左上角的点，然后枚举横着的和竖着的线段，看他们有没有交点就好了。

时间复杂度看起来是 $ O(n^4) $ 的，但是对于每一行来说，与之对应的横线段最多有 $ n $ 个，竖线段最多有 $ m $ 个。

所以时间复杂度是 $ O(n^2m) $ 的。

可以过 Subtask1,2,3,4,5,6，拿到了 $ 72 $ 分。

可能说的有一点难懂，这部分代码我就放一下。

代码

因为我们学校 OJ 比较快，比赛当时这份程序拿了 $ 72 $ 分，但是 luogu 上只拿了 $ 37 $ 分，卡一卡应该也差不多（雾

正解

说了这么多终于说到了。

我们首先可以发现无论是上面寻找行矩阵/列矩阵，还是下面进行匹配的过程，都是 $ n^2m $ 的，无法通过本题，所以上述两部分都需要优化。

优化1

先来优化寻找行矩阵/列矩阵的部分。

我们来看瓶颈在哪里，不难发现是在加入“线段”的过程，我们需要枚举一个点( $ O(nm) $ )，然后向下/右延申线段。

不难发现，其中一部分枚举是重复的。因为当我们找到一个行矩阵时候，这个矩阵去掉最上面/最下面一行，剩下的行矩阵必定合法，列矩阵也是一样。

这个样子，我们就可以将这部分优化到 $ O(nm\log m) $。

为啥有个 $ \log $ ？因为我们在每一行/列中都要对元素进行排序。

优化2

不难发现，这个部分其实就是一个找线段有多少个交点的过程。

我们直接树状数组统计一下就可以了。

其实看起来简单，实际细节还是有亿点的，具体可以看代码。

最终时间复杂度是 $ O(n^2\log n) $。

代码：

这份代码 luogu 上可过，请放心食用。

#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
template<typename T>
using vc=vector<T>;
using ll=long long;
inline int lowbit(int i){ return i&(-i);}
template<typename A>
using pqueue=priority_queue<A,vector<A>,greater<A> >;
inline int read()
{
    int s=0,w=1;char ch;
    while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
struct line
{
    int l,r;
    int wh;
    line(int l=0,int r=0,int wh=0) :l(l),r(r),wh(wh){}
};
struct node
{
    int num;
    int wh;
}b[2501];
bool operator < (line a,line b)
{
    return a.r<b.r;
}
bool operator > (line a,line b)
{
    return a.r>b.r;
}
vc<line>ans1[2502][2502];
vc<line>ans2[2502][2502];
vc<int>vis[2502][2502];
int a[2502][2502];
line num1[2502];
line num2[2502];
int t[2502];
int fa[2502];
int l[2502];
int r[2502];
int n,m;
ll ans;
int find(int num)
{
    if(fa[num]==num) return num;
    return fa[num]=find(fa[num]);
}
void add(int wh)
{
    fa[wh]=l[wh]=r[wh]=wh;
    if(fa[wh-1])
    {
        int num=find(wh-1);
        fa[num]=wh,l[wh]=l[num];
    }
    if(fa[wh+1])
    {
        int num=find(wh+1);
        fa[num]=wh,r[wh]=r[num];
    }
}
void push(int i,int wh,int ma)
{
    int num=find(wh);
    if(num!=wh) return ;
    if(l[wh]==1||r[wh]==ma) return ;
    // printf("%d %d %d\n",i,l[wh],r[wh]);
    vis[l[wh]][r[wh]].push_back(i);
}
void addt(int x,int y)
{
    while(x<=n)
    {
        t[x]+=y;
        x+=lowbit(x);
    }
}
int gett(int x)
{
    int ans=0;
    while(x)
    {
        ans+=t[x];
        x-=lowbit(x);
    }
    return ans;
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++) b[j].num=a[i][j],b[j].wh=j;
        sort(b+1,b+m+1,[](node a,node b){ return a.num<b.num;});
        for(int j=1,k;j<=m;j=k)
        {
            for(k=j;k<=m&&b[j].num==b[k].num;k++);
            for(int y=j;y<k;y++) add(b[y].wh);
            for(int y=j;y<k;y++) push(i,b[y].wh,m);
        }
        for(int i=1;i<=m;i++) fa[i]=0;
    }
    for(int s=1;s<=m;s++) for(int e=s;e<=m;e++) for(unsigned i=0,j;i<vis[s][e].size();i=j)
    {
        for(j=i;j<vis[s][e].size()&&vis[s][e][j]-j==vis[s][e][i]-i;j++);
        for(unsigned k=i;k<j;k++) ans1[vis[s][e][k]][s].push_back(line(vis[s][e][k],vis[s][e][j-1],e));
    }
    for(int i=1;i<=m;i++) for(int j=1;j<=m;j++) vis[i][j].clear();

    for(int j=1;j<=m;j++)
    {
        for(int i=1;i<=n;i++) b[i].num=a[i][j],b[i].wh=i;
        sort(b+1,b+n+1,[](node a,node b){ return a.num<b.num;});
        for(int i=1,k;i<=n;i=k)
        {
            for(k=i;k<=n&&b[i].num==b[k].num;k++);
            for(int x=i;x<k;x++) add(b[x].wh);
            for(int x=i;x<k;x++) push(j,b[x].wh,n);
        }
        for(int i=1;i<=n;i++) fa[i]=0;
    }
    for(int s=1;s<=n;s++) for(int e=s;e<=n;e++) for(unsigned i=0,j;i<vis[s][e].size();i=j)
    {
        for(j=i;j<vis[s][e].size()&&vis[s][e][j]-j==vis[s][e][i]-i;j++);
        for(unsigned k=i;k<j;k++) ans2[s][vis[s][e][k]].push_back(line(vis[s][e][k],vis[s][e][j-1],e));
    }
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
    {
        int tot1=0,tot2=0;
        for(line k:ans1[i][j]) num1[++tot1]=k;
        for(line k:ans2[i][j]) num2[++tot2]=k;
        sort(num1+1,num1+tot1+1,[](line a,line b){ return a.wh<b.wh;});
        sort(num2+1,num2+tot2+1,[](line a,line b){ return a.l<b.l;});
        pqueue<line>que;int now=1;
        for(int k=1;k<=tot1;k++)
        {
            while(now<=tot2&&num2[now].l<=num1[k].wh) addt(num2[now].wh,1),que.push(num2[now]),now++;
            while(que.size()&&que.top().r<num1[k].wh) addt(que.top().wh,-1),que.pop();
            ans+=gett(num1[k].r)-gett(num1[k].l-1);
        }
        while(que.size()) addt(que.top().wh,-1),que.pop();
    }
    printf("%lld\n",ans);
    return 0;
}

感谢观看！