斯特林数

斯特林数（Stirling）

目录

• 斯特林数（Stirling）
  • （一）第一类斯特林数[]
    • 1.定义
    • 2.公式
    • 3.数值表
  • （二）第二类斯特林数{}
    • 1.定义
    • 2.公式
    • 3.数值表
  • （三）联系
  • （四）应用
    • 1.上升幂与下降幂
  • （五）习题
    • 1.bzoj4555
  • （六）附录

这篇写还行，阅读时要注意，里面有很多的错误

5.6Stirling数

当然，最详细的，在\(\ll\)具体数学\(\gg\)里面

（一）第一类斯特林数[]

1.定义

记为 \(S_{1}(n,k)\) ，计算将 \(n\) 个元素排成 \(k\) 个轮换的方案数，其实也就是 \(k\) 个圆

2.公式

• \(S_{1}(0,0)=1，S_{1}(n,0)=0\)
• \(S_{1}(n,1)=(n-1)! ， n>0\) （有\(n!\)种排列，其中每一个元素都可以作为第一个元素）
• \(S_{1}(n,n)=1\)
• \(S_{1}(n,n-1)=\binom{n}{2}\)
• \(S_{1}(n,k)=(n-1)S_{1}(n-1,k)+S_{1}(n-1,k-1)\)，其中 \(n>0\)
  将最后一个元素放入前\(n-1\)个元素分成的 \(S_{1}(n-1,k)\) 个轮换中，有 \(n-1\) 种方法
  为了证明这一点，首先可以验证恰好有 \(j\) 种方式把一个新元素放进 \(j\) 轮换中形成一个 \(j+1\) 轮换 （一个有 \(j\) 个元素的圆中，共有 \(j\) 个间隙），那么只要对所有的 \(k\) 个 \(j\) 求和，就可以得到有 \(n-1\) 种方式将第 \(n\) 个元素放入 \(n-1\) 个元素形成的 \(k\) 个轮换中
• $\sum_{k=0}^{n}S_{1}(n,k)=n! $
  因为排列与轮换安排一一对应，所以 \(S1(n,k)\) 为 \(n\) 个元素恰好包含 \(k\) 个轮换的排列的个数，如果对于所有的 \(k\) 求和 \(S1(n,k)\) ，必定可以得到排列总数 \(n!\)

3.数值表

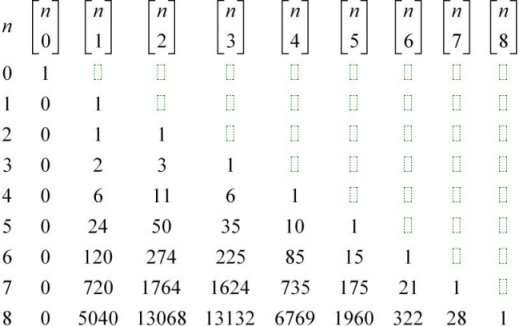
（二）第二类斯特林数{}

1.定义

记为 \(S_{2}(n,k)\)，表示将 \(n\) 个元素划分为 \(k\) 个非空子集的方案数

2.公式

• \(S_{2}(n,0)=0\)，其中 \(n>0\)，而\(S_{2}(0,0)=1\)

• \(S_{2}(n,1)=1\)，其中 \(n>0\)，而\(S_{2}(0,1)=0\)

• \(S_{2}(n,2)=2^{n-1}-1\)，其中 \(n>0\)，而\(S_{2}(0,2)=0\)，对于每个数，有两种集合归属的情况，所以是 \(2^n\) ，去除掉两个全集的情况，就是 \(2^n-2\) ，又因为两个集合没有顺序的关系，所以要除以２

• \(S_{2}(n,k)=kS_{2}(n-1,k)+S_{2}(n-1,k-1)\)，其中 \(n>0\)
  最后一个元素可以自己单独一个集合，也可以与前面的某个非空子集放在一起，有 \(k\) 中放法

• \(S_{2}(n,n-1)=\binom{n}{2}\)

• \(S_{2}(n,n)=1\)

• 然后还有一个很重要的式子：原因详见百度百科

  \[m!S_{2}(n,m)=\sum_{k=0}^{m}(-1)^kC(m,k)(m-k)^n \]

\(m!S_{2}(n,m)\) 表示将\(n\)个不同的球放入\(m\)个编号不同的盒子中，使得没有一个盒子是空的的方案数。然后后面的式子就是一个组合数形式的容斥原理的简单应用。

注意到这个式子是一个卷积的形式，所以我们可以利用NTT在\(O(n\log n)\)的复杂度内，预处理出所有的\(S(n,i),1\leqslant i \leqslant n\)。为什么这个式子可以NTT呢？好像不太明显，我们把组合数拆开，原式化为：

\[S(n,m)=\frac{1}{m!}\sum_{k=0}^{m}(-1)^k\frac{m!}{k!(m-k)!}(m-k)^n \]

整理一下，就可以变成：

\[S(n,m)=\sum_{k=0}^{m}[\frac{(-1)^k}{k!}] \times [\frac{(m-k)^n}{(m-k)!}] \]

这下子，卷积的形式就很明显了，于是我们也就可以用NTT实现了。

code

3.数值表

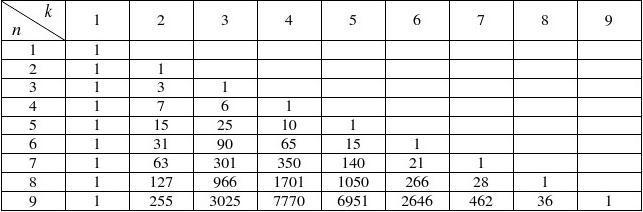
（三）联系

• 轮换数大于等于子集数，即 \(S_{1}(n,k)\geqslant S_{2}(n,k)\)，\(n,k\geqslant0\)
• \(S_{1}(n,n)=S_{2}(n,n)=1\)
• \(S_{1}(n,n-1)=S_{2}(n,n-1)=\binom{n}{2}\)
• \(\sum_{k=0}^{n}S_{1}(n,k)=n!\) ，排列与轮换一一对应
• 反转公式：\(\sum_{k}S_{1}(n,k)S_{2}(k,m)(-1)^{n-k}=[m=n]\)
• 反转公式：\(\sum_{k}S_{2}(n,k)S_{1}(k,m)(-1)^{n-k}=[m=n]\)

（四）应用

1.上升幂与下降幂

为了方便，我们定义

\(\left\lceil x \right\rceil_{n}=x(x+1)(x+2)...(x+n-1)\) （上升幂）

\(\left\lfloor x \right\rfloor_{n}=x(x-1)(x-2)...(x-n+1)\) （下降幂）

那么，我们可以得到

• \(x^{n}=\sum_{k=0}^{n}S_{2}(n,k)\left\lfloor x \right\rfloor_{k}\)，\(n\geqslant0\)
• \(x^{n}=\sum_{k=0}^{n}S_{2}(n,k)(-1)^{n-k}\left\lceil x \right\rceil_{k}\)，\(n\geqslant0\)
• \(\left\lceil x \right\rceil_{n}=\sum_{k=0}^{n}S_{1}(n,k)x^{k}\)，\(n\geqslant0\)
• \(\left\lfloor x \right\rfloor_{n}=\sum_{k=0}^{n}S_{1}(n,k)(-1)^{n-k}x^{k}\)，\(n\geqslant0\)

另外，再拓展一点，对于\(\left\lfloor x \right\rfloor_{k}\)有

\[\left\lfloor x \right\rfloor_{k}=x*(x-1)*...*(x-k+1) \]

\[=\frac{x!}{(x-k)!}=C(x,k)*k! \]

那么，对于第一个式子，我们可以得到

\[x^{n}=\sum_{k=0}^{n}S_{2}(n,k)C(x,k)*k! \]

（五）习题

1.bzoj4555

求

\[f(n)=\sum_{i=0}^{n}\sum_{j=0}^{i}S_{2}(i,j)*2^{j}*(j!) \]

解析：

这道题目与上面的例题没有很大的区别，推导过程也很容易，只是要注意函数的预处理部分那些较小的值

（六）附录

关于反转公式的证明

资料来自维基百科

设

\[P(n)=\displaystyle \sum_k \left[{n \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{n - k} = \delta_{m n} \]

对于 \(P(0)\) 很显然

当 \(n \geq 0\) 时，假设我们已经证出

\[\displaystyle \forall j: 0 \le j \le r，\displaystyle \forall m \in Z: \sum_k \left[{j \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{j - k} = \delta_{m j} \]

那么，就需要证明

\[\displaystyle \forall m \in Z: \sum_k \left[{ {r + 1} \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{r + 1 - k} = \delta_{m \left({r + 1}\right)} \]

证明：

\[\begin{align} &=\displaystyle \sum_k \left[{ {r + 1} \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{r + 1 - k} \\ &=\displaystyle \sum_k \left({\left[{r \atop k - 1}\right] + r \left[{r \atop k}\right]}\right) \left\{ {k \atop m}\right\} \left({-1}\right)^{r + 1 - k}\\ &=\displaystyle \sum_k \left[{r \atop k - 1}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{r + 1 - k} - r \sum_k \left[{r \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{r - k}\\ &=\displaystyle \sum_k \left[{r \atop k - 1}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{r + 1 - k} - r \delta_{m r}\\ &=\displaystyle \sum_k \left[{r \atop k - 1}\right] \left({\left\{ {k - 1 \atop m - 1}\right\} + m \left\{ {k - 1 \atop m}\right\} }\right) \left({-1}\right)^{r + 1 - k} - r \delta_{r m}\\ &=\displaystyle \sum_k \left[{r \atop k - 1}\right] \left\{ {k - 1 \atop m - 1}\right\} \left({-1}\right)^{r - \left({k - 1}\right)}\\ &+ m \sum_k \left[{r \atop k - 1}\right] \left\{ {k - 1 \atop m}\right\} \left({-1}\right)^{r - \left({k - 1}\right)} - r \delta_{r m}\\ &=\displaystyle \delta_{r \left({m - 1}\right)} + m \delta_{r m} - r \delta_{r m}\\ &=\displaystyle \delta_{m \left({r + 1}\right)} + \left({m - r}\right) \delta_{r m}\\ &=\displaystyle \delta_{m \left({r + 1}\right)}\\ \end{align}\]

所以

\[\displaystyle \forall m, n \in Z: \sum_k \left[{n \atop k}\right] \left\{ {k \atop m}\right\} \left({-1}\right)^{n - k} = \delta_{m n} \]