学生:邬代杰
院系:遥感信息工程学院
学号:2019302130329
班级:19D9
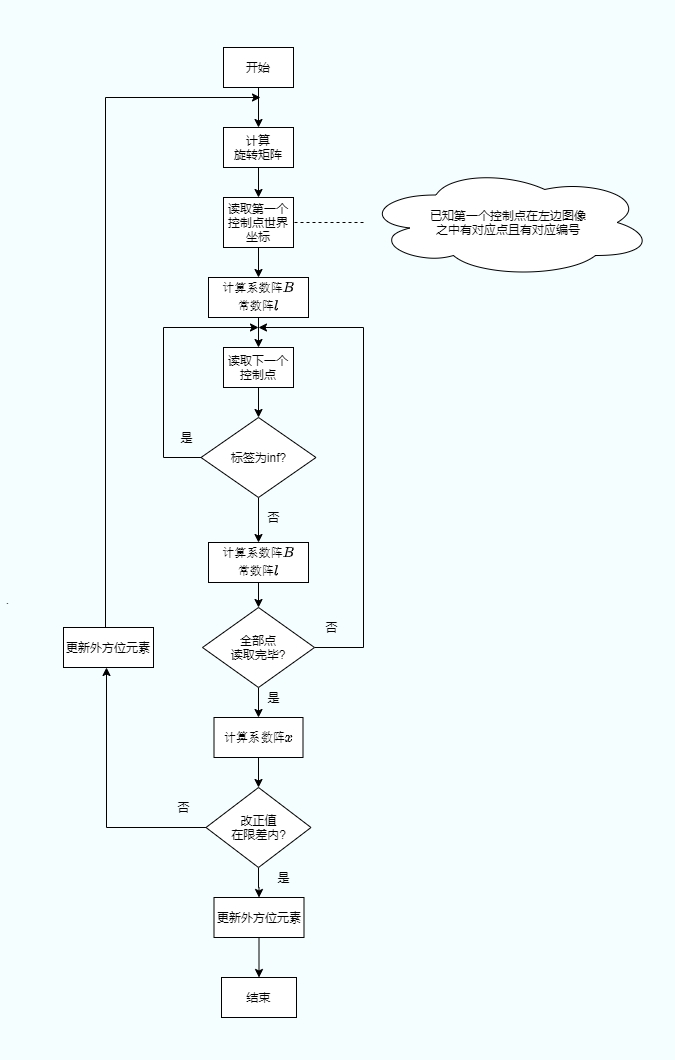
一. 基本原理
1. 寻找控制点坐标
控制点就是圆盘上黑色区域的中心坐标,体现在图像上就是黑色像素集合区域的中心,那我们首先要做的就是提取出黑色像素。由于原图像为RGB彩色图像,佛像与背景、控制点黑色区域与圆盘其他部分对比度较高,故考虑将图像二值化后再进行操作,具体操作应用MATLAB自带函数就可以解决,不再赘述。
2. 对控制点进行编号
提取出控制点坐标后,接下来的任务就是利用已知的控制点编号规则在图像上对控制点进行编号。
注意到控制点是在一个圆盘之上的,即是说:
任意过同一编号组控制点的直线一定都相交于圆盘圆心且过圆心的直线至多与4个控制点中心相交
![]()
又有:投影(相机摄像)不会改变物体的相对位置,并且图片已经消除了畸变,不会出现同一组控制点不在一条直线上的情况。
基于以上事实,我们可以得到将控制点编号的方法:
-
选取两组控制点中各两点,列直线方程;
-
计算两直线相交点作为圆盘中心点;
-
逐点进行遍历并分组:首先任意选取一点作为起始点,然后应用直线拟合对其他点进行判定(即是否为同一组控制点)并记录同一组的控制点的像素坐标,然后不断选取未分组的点进行分组操作,直到全部点分组完毕;
-
将分组后的控制点从外到内进行排序:在分好组的控制点间计算其与中心点之间的棋盘距离,采用冒泡排序以便于同时更新控制点坐标;
-
编号:根据控制点区域大小赋给控制点不同的值(0或1),4个点得到一个二进制数(不满4个点的控制点组舍弃),依此序列计算组号。以0100为例,组号为:\(0\times 2^3+1\times2^2+0\times2^1+0\times2^0=4\). 若组号为\(n\),从外到内的编号依次为:
\[ N=4(n-1)+i-1\quad(i是从外到内点的位置)
\]
至此,编号结束。
3. 计算相机外部参数
采取后方交会计算左右相片各自的外部参数。
后方交会原理:
共线方程
\[\begin{align}
x-x_0&=-f\frac{a_1(X-X_S)+b_1(Y-Y_S)+c_1(Z-Z_S)}{a_3(X-X_S)+b_3(Y-Y_S)+c_3(Z-Z_S)}=-f\frac{\overline{X}}{\overline{Z}}\\
y-y_0&=-f\frac{a_2(X-X_S)+b_2(Y-Y_S)+c_2(Z-Z_S)}{a_3(X-X_S)+b_3(Y-Y_S)+c_3(Z-Z_S)}=-f\frac{\overline{Y}}{\overline{Z}}
\end{align}
\]
其中
\[\begin{align}
R&=\begin{bmatrix}
a_1 & a_2& a_3\\
b_1 & b_2& b_3\\
c_1 & c_2& c_3
\end{bmatrix}\\
&=\begin{bmatrix}
\cos\varphi\cos\kappa-\sin\varphi\sin\omega\sin\kappa & -\cos\varphi\sin\kappa & -\sin\varphi\cos\omega\\
\cos\omega\sin\kappa & \cos\omega\cos\kappa & -\sin\omega\\
\sin\omega\cos\kappa+\cos\varphi\sin\omega\sin\kappa & -\sin\varphi\sin\kappa+\cos\varphi\sin\omega\cos\kappa & \cos\varphi\cos\omega
\end{bmatrix}
\end{align}
\]
\((X,Y,Z)\)为像点世界坐标, \((X_S,Y_S,Z_S)\)为相片外部参数, \((x,y)\)为像点坐标, \((x_0,y_0)\)为像点中心坐标。
由间接平差模型
\[Av=Bx-l
\]
对共线方程线性化后有
\[x^T=\begin{bmatrix}\Delta X_S&\Delta Y_S&\Delta Z_S&\Delta\varphi&\Delta\omega&\Delta\kappa\end{bmatrix}\\
B=\begin{bmatrix}
a_{11}&a_{12}&a_{13}&a_{14}&a_{15}&a_{16}\\
a_{21}&a_{22}&a_{23}&a_{24}&a_{25}&a_{26}
\end{bmatrix}\\
l=\begin{bmatrix}
l_x\\l_y
\end{bmatrix}
\]
其中
\[\begin{equation}
\left\{
\begin{aligned}
a_{11}&=\frac{1}{\overline{Z}}[a_1f+a_3(x-x_0)]\\
a_{12}&=\frac{1}{\overline{Z}}[b_1f+b_3(x-x_0)]\\
a_{13}&=\frac{1}{\overline{Z}}[c_1f+c_3(x-x_0)]\\
a_{21}&=\frac{1}{\overline{Z}}[a_2f+a_3(y-y_0)]\\
a_{22}&=\frac{1}{\overline{Z}}[b_2f+b_3(y-y_0)]\\
a_{23}&=\frac{1}{\overline{Z}}[c_2f+c_3(y-y_0)]
\end{aligned}
\right.
\end{equation}
\]
\[\begin{equation}
\left\{
\begin{aligned}
a_{14}&=(y-y_0)\sin\omega-\{\frac{(x-x_0)}{f}[(x-x_0)\cos\kappa-(y-y_0)\sin\kappa]+f\cos\kappa\}\cos\omega\\
a_{15}&=-f\sin\kappa-\frac{x-x_0}{f}\{(x-x_0)\sin\kappa+(y-y_0)\cos\kappa\}\\
a_{16}&=+(y-y_0)\\
a_{24}&=-(x-x_0)\sin\omega-\{\frac{(y-y_0)}{f}[(x-x_0)\cos\kappa-(y-y_0)\sin\kappa]-f\cos\kappa\}\cos\omega\\
a_{25}&=-f\sin\kappa-\frac{y-y_0}{f}\{(x-x_0)\sin\kappa+(y-y_0)\cos\kappa\}\\
a_{26}&=-(x-x_0)\\
\end{aligned}
\right.
\end{equation}
\]
计算\(x\)的公式为
\[x=(B^TPB)^{-1}BPl
\]
其中\(P\)矩阵为权阵,在本次实习中,各控制点间相互独立且精度相同,故权阵为单位矩阵,变为求
\[x=(B^TB)^{-1}Bl
\]
在MATLAB中表示为
\[x=(B'*B)\text{\\}B*l
\]
在计算出改正值后,不断迭代更新外方位元素平差值直至改正值在限差之内即可。
4. 计算控制点三维坐标
原理:前方交会
已知:
\[\begin{align}
相机内参:&x_0,y_0,f,width,height\\
相片外参:&X_{S1},Y_{S1},Z_{S1},\varphi_1,\omega_1,\kappa_1\\
&X_{S2},Y_{S2},Z_{S2},\varphi_2,\omega_2,\kappa_2\\
同名像点坐标:&(x_1,y_1),(x_2,y_2)
\end{align}
\]
待求:
\[控制点三维坐标:X_p,Y_p,Z_p
\]
过程:
- 计算左右片在地辅坐标系中旋转矩阵的方向余弦:该步骤与后方交会时计算旋转矩阵一致;
\[ R=\begin{bmatrix}
a_1 \quad a_2\quad a_3\\
b_1 \quad b_2\quad b_3\\
c_1 \quad c_2\quad c_3
\end{bmatrix}\\
R'=\begin{bmatrix}
a_1' \quad a_2'\quad a_3'\\
b_1' \quad b_2'\quad b_3'\\
c_1' \quad c_2'\quad c_3'
\end{bmatrix}
\]
- 计算基线分量
\[ B _ { X } = X _ { s2 } - X _ { s1 } \\
B _ { Y } = Y _ { s 2 } - Y _ { s1 } \\
B _ { Z } = Z _ { s 2 } - Z _ { s 1 }
\]
- 计算像点的像空间辅助坐标
\[ \begin{bmatrix}
X\\Y\\Z
\end{bmatrix}
=R\begin{bmatrix}
x_1\\y_1\\-f
\end{bmatrix},
\begin{bmatrix}
X'\\Y'\\Z'
\end{bmatrix}
=R\begin{bmatrix}
x_2\\y_2\\-f
\end{bmatrix}
\]
- 计算投影系数
\[ N=\frac{B_X Z'-B_Z X'}{XZ'-ZX'}\\
N'=\frac{B_X Z-B_Z X}{XZ'-ZX'}
\]
- 计算地面点的左像辅系坐标
\[ \begin{align}
\Delta X&=NX\\
\Delta Y&=(NY+N'Y'+B_Y)/2\\
\Delta Z&=NZ
\end{align}
\]
- 计算地面点的地面坐标
\[ \begin{align}
X_p&=X_{s1}+\Delta X\\
Y_p&=Y_{s1}+\Delta Y\\
Z_p&=Z_{s1}+\Delta Z\\
\end{align}
\]
二. 实现过程
以下均以左边图像为例
1. 寻找控制点
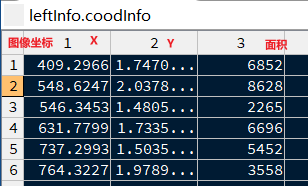
main.m第52~74行:
RGB转灰度图-->灰度图转二值图-->对二值图取质心及面积-->储存于结构体ldftInfo.coodInfo中
2. 寻找圆盘中心点
main.m第76~85行
选定第1,13,28,40点计算中心点坐标-->计算交点(中心点坐标)-->存于ldftInfo.centreInfo
3. 对控制点分组
main.m第87~119行
flag数组用于标记是否分组-->将选择出来的未分组的控制点与中心点进行一次幂拟合,得到系数-->遍历所有控制点,寻找在一条直线上的点-->对有的不足4个元素的数组进行补充-->重复迭代直至遍历所有控制点
4. 对控制点编号
main.m第122~158行
距离中心点的距离从小到大进行排序-->求二进制编码组-->编号-->存于leftInfo.coodInfo第4列(Inf为图中有但未进行编号的控制点,其原因是一组中控制点由于佛像遮挡有丢失,无法编号)
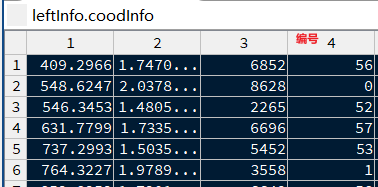
编号校验无误.

5. 优化外部参数
main.m第355~392行
dealA.m计算B矩阵,dealR.m计算旋转矩阵
6. 前方交会反算控制点世界坐标以检验外方位元素计算准确性
main.m第437~469行
寻找左右图同名点后根据前方交会原理一步一步计算即可,不再赘述。
三. 操作说明
1. 运行文件位置说明
请将main.m、dealR.m以及dealA.m放在同一文件夹下,并将该文件夹更改为工作文件夹,然后再运行main.m文件。
2. 文件路径替换
main.m文件中路径需要根据自己的情况更改
第49行:左边图像路径
第167行:右边图像路径
第295行:控制点坐标文件
第303行:内部参数文件
第317行:外部参数初值文件
3. MATLAB工作区变量说明
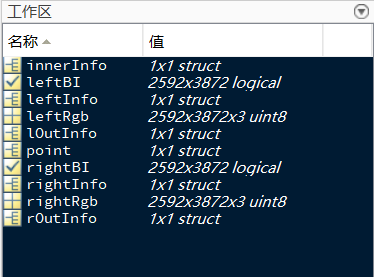
innerInfo内部参数
leftBI rightBI二值化图像
leftRGB rightRGB读取的图像
leftInfo rightInfo左右图片点的信息,包括.coodInfo (像点坐标)以及centreInfo(中心点坐标)
lOutInfo rOutInfo外部参数
point控制点信息,包括.data(数据)和.textdata(文件头)
其余多余变量均已清除。
着重介绍一下point.data结构,它各列代表的信息如下表:
| 列数 |
1 |
2 |
3 |
4 |
5 |
| 含义 |
控制点编号 |
文件读取的X |
文件读取的Y |
文件读取的Z |
控制点类别 |
| 6 |
7 |
8 |
9 |
10 |
11 |
| 前方交会的X' |
前方交会的Y' |
前方交会的Z' |
X-X' |
Y-Y' |
Z-Z' |
其中第6~11列中的控制点,若没有同名点与之对应,则全部赋值为0.
第61行第9~11列数据为累积误差。
四. 结论分析
考虑到求解控制点像点坐标时开运算、闭运算带来的位置偏差和矩阵运算时的精度误差,这个结果是在可以接受的范围内的。在计算过程中,要注意到各个参数的意义,套用公式时要明白其中的原理,特别是各坐标系之间的转换关系,不然很可能会出现某些结果异常的情况,找bug时是十分痛苦的(T x T)
最后附上代码结构
五. 实习成果
实习MATLAB代码:点击下载
高山仰止, 景行行止; 虽不能至, 心向往之.







