转载-复变函数和积分变换(Complex Function I)
复变函数和积分变换(Complex Function I)
复变函数和积分变换(Complex Function II)
复变函数和积分变换(Integral Transform)
参考文献:
mooc国防科技大学《复变函数》
王忠仁、张静《工程数学:复变函数和积分变换》
焦红伟、尹景本《复变函数与积分变换》
梁昆淼《数学物理方法》
复数与复变函数
复数(Complex Number)
复数(Complex Number):形如
z = x + i y ( x , y ∈ R ) z=x+\text{i}y\quad (x,y\in\R) z=x+iy(x,y∈R),其中 i \text{i} i 满足 i 2 = − 1 \text{i}^2=-1 i2=−1 称为虚数单位, x x x 和 y y y 分别称为复数的实部和虚部,记作 x = Re z , y = Im z x=\text{Re }z,y=\text{Im }z x=Re z,y=Im z。
如果 z = i y z=\text{i}y z=iy 称为纯虚数, z = x z=x z=x 看做实数。
如果两复数实部和虚部分别相等,则两复数相等。
复数域(Complex Number Field): C = { z ∣ z = z = x + i y , x , y ∈ R } \Complex=\{z|z=z=x+\text{i}y,\ x,y\in\R\} C={z∣z=z=x+iy, x,y∈R}
复平面(Complex Plane):由于一个复数与 z = x + i y z=x+\text{i}y z=x+iy 与有序实数对 ( x , y ) (x,y) (x,y) 一一对应
x O y xOy xOy 平面 ⟺ \iff ⟺ 复平面 C \Complex C
复数 z = x + i y ⟺ R 2 z=x+\text{i}y \iff \R^2 z=x+iy⟺R2上的点 P ( x , y ) ⟺ R 2 P(x,y) \iff \R^2 P(x,y)⟺R2 上的向量 O P → \overrightarrow{OP} OP
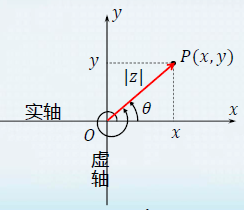
复数的模(modulus):向量的长度称为复数的模,记作 ∣ z ∣ = x 2 + y 2 |z|=\sqrt{x^2+y^2} ∣z∣=x2+y2
复数的幅角(argument angle): O x Ox Ox 轴到 O P → \overrightarrow{OP} OP 沿逆时针方向所形成的角 Arg z = θ + 2 k π ( k ∈ Z ) \text{Arg }z=θ+2kπ\quad(k\in \Z) Arg z=θ+2kπ(k∈Z)
幅角的主值(principal argument angle):辐角 Arg z = arg z + 2 k π ( k ∈ Z ) \text{Arg }z=\arg z+2kπ\quad(k\in \Z) Arg z=argz+2kπ(k∈Z),主值可取 arg z ∈ [ 0 , 2 π ) \arg z\in[0,2π) argz∈[0,2π) 或 arg z ∈ ( − π , π ] \arg z\in(-π,π] argz∈(−π,π]
由于反正切函数 arctan θ ∈ ( − π / 2 , π / 2 ) \arctan θ \in(-π/2,π/2) arctanθ∈(−π/2,π/2),于是分段求出辐角主值 arg z ∈ ( − π , π ] \arg z\in(-π,π] argz∈(−π,π]
arg z = { arctan y x if x > 0 (I,IV) π 2 if x = 0 , y > 0 arctan y x + π if x < 0 , y ⩾ 0 (II) − π 2 if x = 0 , y < 0 arctan y x − π if x < 0 , y < 0 (III) \arg z=
复数的三角表示: z = ∣ z ∣ ( cos θ + i sin θ ) ( θ = Arg z ) z=|z|(\cosθ+\text{i}\sin θ)\quad(θ=\text{Arg }z) z=∣z∣(cosθ+isinθ)(θ=Arg z)
复数的指数表示:由欧拉公式 e i θ = cos θ + i sin θ \boxed{e^{iθ}=\cosθ+\text{i}\sin θ} eiθ=cosθ+isinθ 得到
z = ∣ z ∣ e i θ z=|z|e^{iθ} z=∣z∣eiθ
-
复数的代数运算(Arithmetic with Complex Numbers)
设 z 1 = x 1 + i y 1 , z 2 = x 2 + i y 2 z_1=x_1+\text{i}y_1,\ z_2=x_2+\text{i}y_2 z1=x1+iy1, z2=x2+iy2
z 1 + z 2 = ( x 1 + x 2 ) + i ( y 1 + y 2 ) z_1+z_2=(x_1+x_2)+\text{i}(y_1+y_2) z1+z2=(x1+x2)+i(y1+y2)
z 1 z 2 = ( x 1 x 2 − y 1 y 2 ) + i ( x 1 y 2 + x 2 y 1 ) z_1z_2=(x_1x_2-y_1y_2)+\text{i}(x_1y_2+x_2y_1) z1z2=(x1x2−y1y2)+i(x1y2+x2y1)
由加法和乘法可以定义减法和除法
z 1 − z 2 = ( x 1 − x 2 ) + i ( y 1 − y 2 ) z_1-z_2=(x_1-x_2)+\text{i}(y_1-y_2) z1−z2=(x1−x2)+i(y1−y2)
z 1 z 2 = x 1 x 2 + y 1 y 2 x 2 2 + y 2 2 + i x 2 y 1 − x 1 y 2 x 2 2 + y 2 2 \dfrac{z_1}{z_2}=\dfrac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+\text{i}\dfrac{x_2y_1-x_1y_2}{x_2^2+y_2^2} z2z1=x22+y22x1x2+y1y2+ix22+y22x2y1−x1y2
由上述规定,可以验证:加法、乘法满足交换律与结合律,乘法对加法满足分配律。由此可知,在实数域里由这些规律推得的恒等式在复数里仍然有效。复数集关于四则运算是封闭的,其代数结构是域。 -
共轭复数(conjugate complex number)及性质: z ˉ = x − i y \bar z=x-\text{i}y zˉ=x−iy
(1) z 1 ± z 2 ‾ = z ˉ 1 ± z ˉ 2 , z 1 z 2 ‾ = z ˉ 1 z ˉ 2 , z 1 / z 2 ‾ = z ˉ 1 / z ˉ 2 \overline{z_1± z_2}=\bar z_1± \bar z_2,\ \overline{z_1z_2}=\bar z_1\bar z_2,\ \overline{z_1/z_2}=\bar z_1/\bar z_2 z1±z2=zˉ1±zˉ2, z1z2=zˉ1zˉ2, z1/z2=zˉ1/zˉ2
(2) z ˉ ˉ = z \bar{\bar z}=z zˉˉ=z
(3) z z ˉ = ∣ z ∣ 2 = ∣ z ˉ ∣ 2 z\bar z=|z|^2=|\bar z|^2 zzˉ=∣z∣2=∣zˉ∣2
(4) x = 1 2 ( z + z ˉ ) , y = 1 2 i ( z − z ˉ ) x=\dfrac{1}{2}(z+\bar z),\ y=\dfrac{1}{2i}(z-\bar z) x=21(z+zˉ), y=2i1(z−zˉ) -
复数的性质
(1) z 1 z 2 = ∣ z 1 ∣ ∣ z 2 ∣ [ cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ] z_1z_2=|z_1||z_2|[\cos(θ_1+θ_2)+\text{i}\sin(θ_1+θ_2)] z1z2=∣z1∣∣z2∣[cos(θ1+θ2)+isin(θ1+θ2)]
(2) Arg ( z 1 z 2 ) = Arg z 1 + Arg z 2 \text{Arg }(z_1z_2)=\text{Arg }z_1+\text{Arg }z_2 Arg (z1z2)=Arg z1+Arg z2
Arg ( z 1 / z 2 ) = Arg z 1 − Arg z 2 \text{Arg }(z_1/z_2)=\text{Arg }z_1-\text{Arg }z_2 Arg (z1/z2)=Arg z1−Arg z2
(3) ∣ z 1 z 2 ∣ = ∣ z 1 ∣ ∣ z 2 ∣ , ∣ z 1 / z 2 ∣ = ∣ z 1 ∣ / ∣ z 2 ∣ |z_1z_2|=|z_1||z_2|,|z_1/z_2|=|z_1|/|z_2| ∣z1z2∣=∣z1∣∣z2∣,∣z1/z2∣=∣z1∣/∣z2∣
(5) ∣ z 1 + z 2 ∣ 2 = ∣ z 1 ∣ 2 + ∣ z 2 ∣ 2 + 2 Re ( z 1 z ˉ 2 ) |z_1+ z_2|^2=|z_1|^2+|z_2|^2+2\text{Re }(z_1\bar z_2) ∣z1+z2∣2=∣z1∣2+∣z2∣2+2Re (z1zˉ2)
三角不等式: ∣ ∣ z 1 ∣ − ∣ z 2 ∣ ∣ ⩽ ∣ z 1 ± z 2 ∣ ⩽ ∣ z 1 ∣ + ∣ z 2 ∣ ||z_1|-|z_2||⩽ |z_1± z_2| ⩽ |z_1|+|z_2| ∣∣z1∣−∣z2∣∣⩽∣z1±z2∣⩽∣z1∣+∣z2∣ -
乘幂(power)
设复数 z = ∣ z ∣ ( cos θ + i sin θ ) = ∣ z ∣ e i θ ( θ = Arg z ) z=|z|(\cos θ+i\sin θ)=|z|e^{iθ} \quad(θ=\text{Arg }z) z=∣z∣(cosθ+isinθ)=∣z∣eiθ(θ=Arg z)
由三角函数的性质可知 z n = ∣ z ∣ n [ cos ( n θ ) + i sin ( n θ ) ] = ∣ z ∣ n e i n θ z^n=|z|^n[\cos(nθ)+i\sin(nθ)]=|z|^ne^{inθ} zn=∣z∣n[cos(nθ)+isin(nθ)]=∣z∣neinθ
特别的有 ( cos θ + i sin θ ) n = cos ( n θ ) + i sin ( n θ ) (\cos θ+i\sin θ)^n=\cos(nθ)+i\sin(nθ) (cosθ+isinθ)n=cos(nθ)+isin(nθ) ,这就是De Moivre formula -
n次方根(n-th root)
将满足 z = w n z=w^n z=wn 的 w w w称为 z z z的 n n n次方根,记为 w = z n ( n = 1 , 2 , ⋯ ) w=\sqrt[n]{z}\quad(n=1,2,\cdots) w=nz(n=1,2,⋯)
w = ∣ z ∣ n ( cos θ n + i sin θ n ) = ∣ z ∣ n ( cos φ + i sin φ ) = ∣ z ∣ n e i φw=n∣z∣(cosnθ+isinnθ)=n∣z∣(cosφ+isinφ)=n∣z∣eiφ
其中 φ = arg z + 2 k π n φ=\dfrac{\arg z+2kπ}{n} φ=nargz+2kπ
当 k = 0 , 1 , 2 , ⋯ , n − 1 k=0,1,2,⋯, n-1 k=0,1,2,⋯,n−1 时,存在 n n n 个辐角各不相等的根,在几何上, z n \sqrt[n]{z} nz表示位于复平面上以原点 O O O 为圆心,以 ∣ z ∣ n \sqrt[n]{|z|} n∣z∣ 为半径的内接正 n n n 边形的顶点。 -
复球面与无穷远点(complex sphere & point at infinity)
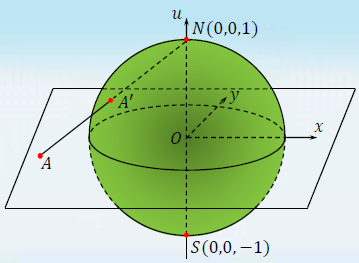
复球面方程 Σ : x 2 + y 2 + u 2 = 1 Σ:x^2+y^2+u^2=1 Σ:x2+y2+u2=1
对于复平面上任意一点 z,如果用直线连接点 z和复球面北极 N,那么该直线一定与复球面相交于异于N点的另一点 A ′ A' A′,复平面上的点 A ( x , y ) A(x,y) A(x,y) 与复球面上的点 A ′ ( x ′ , y ′ , u ′ ) A'(x',y',u') A′(x′,y′,u′) 一一对应
z = x + i y = x ′ + i y ′ 1 − u ′ z=x+\text{i}y=\dfrac{x'+\text {i}y'}{1-u'} z=x+iy=1−u′x′+iy′
x ′ = z + z ˉ ∣ z ∣ 2 + 1 , y ′ = z − z ˉ i ( ∣ z ∣ 2 + 1 ) , u ′ = ∣ z ∣ 2 − 1 ∣ z ∣ 2 + 1 x'=\dfrac{z+\bar z}{|z|^2+1},\ y'=\dfrac{z-\bar z}{i(|z|^2+1)},\ u'=\dfrac{|z|^2-1}{|z|^2+1} x′=∣z∣2+1z+zˉ, y′=i(∣z∣2+1)z−zˉ, u′=∣z∣2+1∣z∣2−1
定义北极 N ( 0 , 0 , 1 ) N(0,0,1) N(0,0,1) 在复平面上对应点为无穷远点,记为 ∞ ∞ ∞
复平面加上无穷远点后称为扩充复平面(extended complex plane)
关于 ∞ ∞ ∞ 的运算法则:
∣ ∞ ∣ = + ∞ a + ∞ = ∞ + a = ∞ a ⋅ ∞ = ∞ ⋅ a = ∞ a / 0 = ∞ ( a ≠ 0 ) , a / ∞ = 0 ( a ≠ ∞ ) |∞|=+∞ \\ a+∞=∞+a=∞ \\ a\cdot∞=∞\cdot a=∞ \\ a/0=∞(a\neq 0),\quad a/∞=0(a\neq ∞) ∣∞∣=+∞a+∞=∞+a=∞a⋅∞=∞⋅a=∞a/0=∞(a=0),a/∞=0(a=∞)
其他关于 ∞ ∞ ∞的运算无定义。 -
几何方程复数表示
复数表示圆的一般方程: a ( x 2 + y 2 ) + b x + c y + d = 0 ( a , b , c , d ∈ R , a ≠ 0 ) a(x^2+y^2)+bx+cy+d=0\quad(a,b,c,d\in\R,\ a\neq 0) a(x2+y2)+bx+cy+d=0(a,b,c,d∈R, a=0)
⟹ a z z ˉ + β ˉ z + β z ˉ + d = 0 , β = 1 2 ( b + i c ) \implies az\bar z+\barβ z+β \bar z+d=0,\quadβ=\frac{1}{2}(b+\text{i}c) ⟹azzˉ+βˉz+βzˉ+d=0,β=21(b+ic)
过复平面上不同两点 a , b a,b a,b 的直线: Im z − a z − b = 0 \text{Im }\dfrac{z-a}{z-b}=0 Im z−bz−a=0
过不共线三点 a , b , c a,b,c a,b,c 的圆的方程: Im ( z − b z − a ⋅ c − a c − b ) = 0 \text{Im }(\dfrac{z-b}{z-a}\cdot\dfrac{c-a}{c-b})=0 Im (z−az−b⋅c−bc−a)=0
平面点集(Planar Point Set)
-
邻域(neighborhood)和去心邻域:设 z 0 z_0 z0为一个定点, ρ > 0 ρ>0 ρ>0
U ( z 0 , ρ ) = { z ∣ ∣ z − z 0 ∣ < ρ , z ∈ C } U ˚ ( z 0 , ρ ) = { z ∣ 0 < ∣ z − z 0 ∣ < ρ , z ∈ C } U(z_0,ρ)=\{z∣|z−z_0|<ρ,z\in\Complex\} \\ \mathring{U}(z_0,ρ)=\{z∣0<|z−z_0|<ρ,z\in\Complex\} U(z0,ρ)={z∣∣z−z0∣<ρ,z∈C}U˚(z0,ρ)={z∣0<∣z−z0∣<ρ,z∈C} -
点与点集的关系:任意一点 z 0 ∈ C z_0\in\Complex z0∈C与任意一点集 E ⊂ C E⊂\Complex E⊂C
内点(interior point): ∃ ρ > 0 , U ( z 0 , ρ ) ⊂ E ∃ ρ>0,U(z_0,ρ)⊂ E ∃ρ>0,U(z0,ρ)⊂E
外点(exterior point): ∃ ρ > 0 , U ( z 0 , ρ ) ∩ E = ∅ ∃ ρ>0,U(z_0,ρ)∩ E=\empty ∃ρ>0,U(z0,ρ)∩E=∅
边界点(boundary point):若 z 0 z_0 z0 的任一邻域 U ( z 0 , ρ ) U(z_0,ρ) U(z0,ρ) 中既含 E E E 的点也含不是 E E E 的点,则称 z 0 z_0 z0为 E E E 的边界,记作 ∂ E ∂ E ∂E
聚点(point of accumulation): ∀ ρ > 0 , U ˚ ( z 0 , ρ ) ∩ E ≠ ∅ ∀ ρ>0,\mathring{U}(z_0,ρ)∩ E\neq \empty ∀ρ>0,U˚(z0,ρ)∩E=∅
孤立点(isolated point): ∃ ρ > 0 , z 0 ∈ E , U ˚ ( z 0 , ρ ) ∩ E = ∅ ∃ ρ>0,z_0\in E,\mathring{U}(z_0,ρ)∩ E= \empty ∃ρ>0,z0∈E,U˚(z0,ρ)∩E=∅

-
定义一些重要的点集
开集: ∀ z 0 ∈ E ∀ z_0\in E ∀z0∈E, z 0 z_0 z0 都是E的内点
闭集: E E E 的全部聚点都属于 E E E
有界集: ∃ U ( z 0 , ρ ) , E ⊂ U ( z 0 , ρ ) ∃ U(z_0,ρ),E⊂ U(z_0,ρ) ∃U(z0,ρ),E⊂U(z0,ρ),点集 E E E为有界集
无界集:不是有界集的点集
连通集:点集E内任何两点都可以用折线连接起来,且该折线上的点都属于E -
区域和曲线
区域(或开区域):连通的开集
闭区域:开区域连同它的边界一起构成的点集 E ˉ = E ∪ ∂ E \bar E=E∪∂ E Eˉ=E∪∂E
定义:设 x ( t ) x(t ) x(t)与 y ( t ) y (t ) y(t) 是定义在区间 [ α , β ] [α ,β ] [α,β]上的实函数,曲线 C C C 在复平面上的点集 z ( t ) = x ( t ) + i y ( t ) z(t) = x(t) + i y(t) z(t)=x(t)+iy(t) , z ( α ) z(α ) z(α) 与 z ( β ) z(β ) z(β) 分别称为曲线 C C C 的起点与终点。曲线C 的方向规定为参数t 增加的方向,曲线C 的反向曲线记为 C − C^- C−
连续曲线(Continuous curve): x ( t ) x(t ) x(t)与 y ( t ) y (t ) y(t) 在区间 [ α , β ] [α ,β ] [α,β]上连续
闭曲线(Closed curve):若 z ( α ) = z ( β ) z(α ) = z(β ) z(α)=z(β),则称 C C C为闭曲线
简单曲线(Simple curve):当且仅当 t 1 = t 2 t_1=t_2 t1=t2时, z ( t 1 ) = z ( t 2 ) z(t_1)=z(t_2) z(t1)=z(t2)
Jordon 曲线:连续的简单曲线
光滑曲线(Smooth curve): x ( t ) x(t ) x(t)与 y ( t ) y (t ) y(t) 在区间 [ α , β ] [α ,β ] [α,β]有连续导数,且 z ′ ( t ) ≠ 0 z'(t)\neq 0 z′(t)=0。称由有限条光滑曲线首尾连接而成的曲线为逐段光滑曲线(Piecewise smooth curve)。
为方便起见,称逐段光滑的闭曲线为围线.关于围线的方向规定为:逆时针方向为正向,顺时针方向为负向。
Jordan 定理:任意一条 Jordon 闭曲线C 必将复平面唯一地分成 D 1 , C , D 2 D_1,C,D_2 D1,C,D2 三个点集,使它们满足:
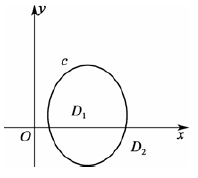
(1) 彼此不相交;
(2) D 1 D_1 D1 是一个有界区域(称为曲线C 的内部);
(3) D 2 D_2 D2 是一个无界区域(称为曲线C 的外部);
(4) C C C 既是 D 1 D_1 D1 的边界又是 D 2 D_2 D2 的边界;
(5) 若简单折线(指满足简单曲线定义的折线) Γ Γ Γ 的一个端点属于 D 1 D_1 D1,另一个端点属于 D 2 D_2 D2,则 Γ Γ Γ 必与 C C C 相交.
设D 为区域,若D 中任意一条 Jordon 闭曲线的内部仍属于D ,则称D 为单连通区域(simply connected region),不是单连通区域的区域称为多连通区域(multiply connected region)。

-
无穷远点的邻域:设 ρ > 0 ρ>0 ρ>0,在扩充复平面上
U ( ∞ , ρ ) = { z ∣ ∣ z ∣ > ρ , z ∈ C ∞ } U(∞,ρ)=\{z||z|>ρ,z\in\Complex_{∞}\} U(∞,ρ)={z∣∣z∣>ρ,z∈C∞}
几何意义:表示曲线 ∣ z ∣ = ρ | z |= ρ ∣z∣=ρ 的外部。
在扩充复平面上,若一个区域内的每一条Jordon 闭曲线的内部或外部(包含无穷远点)都属于这个区域,则称该区域为单连通区域.称不是单连通区域的区域为复连通区域。
复变函数(Complex Function)
-
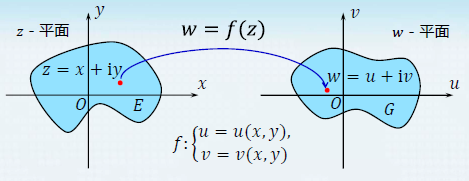
复变函数:设 E E E 为复平面上的点集 w = f ( z ) , z ∈ E w=f(z),z\in E w=f(z),z∈E ,定义域为 E E E,值域为 G G G
若对映射 f f f 只有一个确定的w与z 对应,则称 w = f ( z ) w = f (z) w=f(z)为单值函数,如 w = z 2 w=z^2 w=z2。否则,称 w = f ( z ) w = f (z) w=f(z)为多值函数,如 w = Arg z , w = z w=\text{Arg }z,w=\sqrt{z} w=Arg z,w=z。
设 z = x + i y , w = u + i v z=x+iy,w=u+iv z=x+iy,w=u+iv,复变函数的实部与虚部均可用二元实值函数来表示 w = f ( z ) = u ( x , y ) + i v ( x , y ) w=f(z)=u(x,y)+iv(x,y) w=f(z)=u(x,y)+iv(x,y)
因此,研究复变函数可以转化为研究二元实值函数
由于复变函数 w = f ( z ) w = f (z) w=f(z)的几何图形需在四维空间里考虑,所以,不可能有像实值函数 y = f ( x ) y = f (x) y=f(x) 与 z = f ( x , y ) z = f (x, y) z=f(x,y)的那种直观的感觉。为了赋予复变函数几何解释,复变函数 w = f ( z ) , z ∈ E w=f(z),z\in E w=f(z),z∈E可看作 z z z 平面点集 E E E 到 w w w 平面点集 G G G 的映射
-
极限(limit):设复变函数 w = f ( z ) w=f(z) w=f(z)在 z 0 z_0 z0的某个去心邻域 U ˚ ( z 0 , ρ ) \mathring U(z_0,ρ) U˚(z0,ρ) 内有定义, A A A 为复常数
若 ∀ ϵ > 0 , ∃ δ > 0 ( δ < ρ ) ∀ϵ>0,∃δ>0(δ<ρ) ∀ϵ>0,∃δ>0(δ<ρ),使得 0 < ∣ z − z 0 ∣ < δ 0<|z-z_0|<δ 0<∣z−z0∣<δ时,总有 ∣ f ( z ) − A ∣ < ϵ |f(z)-A|<ϵ ∣f(z)−A∣<ϵ,则称当 z z z趋近于 z 0 z_0 z0时 A A A为 f ( z ) f(z) f(z)的极限,并记作 lim z → z 0 f ( z ) = A \lim\limits_{z\to z_0}f(z)=A z→z0limf(z)=A 或 f ( z ) → A ( z → z 0 ) f(z)\to A(z\to z_0) f(z)→A(z→z0)
极限存在的充要条件:设 w = f ( z ) = u ( x , y ) + i v ( x , y ) , A = u 0 + i v 0 , z 0 = x 0 + i y 0 w=f(z)=u(x,y)+iv(x,y),A=u_0+iv_0,z_0=x_0+iy_0 w=f(z)=u(x,y)+iv(x,y),A=u0+iv0,z0=x0+iy0则
lim z → z 0 f ( z ) = A ⟺ lim ( x , y ) → ( x 0 , y 0 ) u ( x , y ) = u 0 , lim ( x , y ) → ( x 0 , y 0 ) v ( x , y ) = v 0 \lim\limits_{z\to z_0}f(z)=A\iff \lim\limits_{(x,y)\to (x_0,y_0)}u(x,y)=u_0,\lim\limits_{(x,y)\to (x_0,y_0)}v(x,y)=v_0 z→z0limf(z)=A⟺(x,y)→(x0,y0)limu(x,y)=u0,(x,y)→(x0,y0)limv(x,y)=v0
极限运算法则:设 lim z → z 0 f ( z ) = A , lim z → z 0 g ( z ) = B \lim\limits_{z\to z_0}f(z)=A,\lim\limits_{z\to z_0}g(z)=B z→z0limf(z)=A,z→z0limg(z)=B
lim z → z 0 [ f ( z ) ± g ( z ) ] = A ± B \lim\limits_{z\to z_0}[f(z)± g(z)]=A± B z→z0lim[f(z)±g(z)]=A±B
lim z → z 0 f ( z ) g ( z ) = A B \lim\limits_{z\to z_0}f(z)g(z)=AB z→z0limf(z)g(z)=AB
lim z → z 0 f ( z ) / g ( z ) = A / B \lim\limits_{z\to z_0}f(z)/g(z)=A/B z→z0limf(z)/g(z)=A/B -
连续(continuous):若 lim z → z 0 f ( z ) = f ( z 0 ) \lim\limits_{z\to z_0}f(z)=f(z_0) z→z0limf(z)=f(z0),则 w = f ( z ) w=f(z) w=f(z)在 z 0 z_0 z0处连续
若 f ( z ) f(z) f(z)在点集 E E E的每一个聚点连续,则 f ( z ) f(z) f(z)在 E E E连续
连续的充要条件: f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y)在 z 0 = x 0 + i y 0 z_0=x_0+iy_0 z0=x0+iy0处连续 ⟺ u ( x , y ) , v ( x , y ) \iff u(x,y),v(x,y) ⟺u(x,y),v(x,y) 在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处连续
连续函数的性质
(1) 连续函数的和、差、积、商(分母不为0)是连续函数;
(2) 连续函数的复合函数是连续函数.
若函数 f ( z ) f(z) f(z)在有界闭区域 D ˉ \bar D Dˉ上连续,则
(1) f ( z ) f(z) f(z)在 D ˉ \bar D Dˉ上为有界函数;
(2) ∣ f ( z ) ∣ |f(z)| ∣f(z)∣ 在 D ˉ \bar D Dˉ上能取到最大值与最小值,即有 z 1 , z 2 ∈ D ˉ z_1,z_2\in\bar D z1,z2∈Dˉ, ∀ z ∈ D ˉ , ∣ f ( z 1 ) ∣ ⩽ ∣ f ( z ) ∣ ⩽ ∣ f ( z 2 ) ∣ ∀ z\in\bar D,|f(z_1)|⩽ |f(z)|⩽|f(z_2)| ∀z∈Dˉ,∣f(z1)∣⩽∣f(z)∣⩽∣f(z2)∣
(3) f ( z ) f(z) f(z) 在 D ˉ \bar D Dˉ 上一致连续,即 ∀ ϵ > 0 , ∃ δ > 0 ∀ϵ>0,∃δ>0 ∀ϵ>0,∃δ>0,使得当 ∣ z 1 − z 2 ∣ < δ ( z 1 , z 2 ∈ D ˉ ) |z_1-z_2|<δ(z_1,z_2\in\bar D) ∣z1−z2∣<δ(z1,z2∈Dˉ)时,有 ∣ f ( z 1 ) − f ( z 2 ) ∣ < ϵ |f(z_1)-f(z_2)|<ϵ ∣f(z1)−f(z2)∣<ϵ
解析函数(Analytic Function)
导数和解析函数
-
导数(Derivative)
(1) 复变函数 w = f ( z ) , z ∈ D w=f(z),z\in D w=f(z),z∈D在 z 0 z_0 z0处的导数定义为 lim Δ z → 0 f ( z 0 + Δ z ) − f ( z 0 ) Δ z \lim\limits_{Δ z\to0}\dfrac{f(z_0+Δ z)-f(z_0)}{Δ z} Δz→0limΔzf(z0+Δz)−f(z0) 可记作 f ′ ( z 0 ) , f ′ ( z ) ∣ z = z 0 , d f ( z ) d z ∣ z = z 0 f'(z_0), f'(z)|_{z=z_0},\dfrac{\mathrm{d}f(z)}{\mathrm{d}z}|_{z=z_0} f′(z0),f′(z)∣z=z0,dzdf(z)∣z=z0
(2) 如果函数在定义域D内处处可导,则称函数在 D内可导
(3) 与实函数的一致,复变函数的微分 d w = f ′ ( z ) d z \mathrm{d}w=f'(z)\mathrm{d}z dw=f′(z)dz
(4) 设 u = u ( z ) , v = v ( z ) u=u(z),v=v(z) u=u(z),v=v(z)都可导
( u ± v ) ′ = u ′ ± v ′ (u± v)'=u'± v' (u±v)′=u′±v′
( u v ) ′ = u ′ v + u v ′ (uv)'=u'v+uv' (uv)′=u′v+uv′
( u v ) ′ = u ′ v − u v ′ v 2 ( v ≠ 0 ) (\dfrac{u}{v})'=\dfrac{u'v-uv'}{v^2}(v\neq0) (vu)′=v2u′v−uv′(v=0)
复合函数求导法则: f ′ ( z ) = f ′ ( w ) g ′ ( z ) , w = g ( z ) f'(z)=f'(w)g'(z),w=g(z) f′(z)=f′(w)g′(z),w=g(z)
反函数求导: [ f − 1 ( z ) ] ′ = 1 f ′ ( z ) [f^{-1}(z)]'=\dfrac{1}{f'(z)} [f−1(z)]′=f′(z)1,其中 f ( z ) f(z) f(z)为单值函数 -
解析函数(analytic function)
(1) 设函数 w = f ( z ) , z ∈ D w=f(z),z\in D w=f(z),z∈D,对于点 z 0 ∈ D z_0\in D z0∈D,若 ∃ U ( z 0 , ρ ) ∃ U(z_0,ρ) ∃U(z0,ρ),使得函数 f ( z ) f (z) f(z) 在该邻域内处处可导,则称函数 f ( z ) f (z) f(z)在点 z 0 z_0 z0 解析(analytic)。此时称点 z 0 z_0 z0为函数的解析点(analytic point)。若函数 f ( z ) f (z) f(z)在点 z 0 z_0 z0 不解析,则称 z 0 z_0 z0为奇点(singular point)。
(2) 若函数 f ( z ) f (z) f(z) 在区域D内每一点都解析,则称函数 f ( z ) f (z) f(z)在区域D内解析, f ( z ) f (z) f(z)为区域D内的解析函数,区域D又称为函数 f (z)的解析区域或解析域。
(3) 解析与可导的关系:函数在一点解析与函数在该点可导不是一回事,函数在一个区域内解析与该函数在这个区域内处处可导则等价。
解析函数的性质
(1) 解析函数的和、差、积、商(分母不为0)是解析函数;
(2) 解析函数的复合函数是解析函数. -
函数解析的充要条件
函数 f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y) 在区域D内为解析函数的充分必要条件是:
(1) u ( x , y ) u(x, y) u(x,y) 与 v ( x , y ) v(x, y) v(x,y) 在D内可微分 1
(2) 且满足 柯西-黎曼条件 (Cauchy-Riemann,C-R)
∂ u ∂ x = ∂ v ∂ y , ∂ u ∂ y = − ∂ v ∂ x \dfrac{∂u}{∂x}=\dfrac{∂v}{∂y},\dfrac{∂u}{∂y}=-\dfrac{∂v}{∂x} ∂x∂u=∂y∂v,∂y∂u=−∂x∂v
充分性证明:设 z = x + i y z=x+iy z=x+iy是D内任意一点,设 Δ z = Δ x + i Δ y , f ′ ( z ) = a + i b Δz=Δx+iΔy,f'(z)=a+ib Δz=Δx+iΔy,f′(z)=a+ib
Δ f = Δ u + i Δ v = ( ∂ u ∂ x Δ x + ∂ u ∂ y Δ y ) + i ( ∂ v ∂ x Δ x + ∂ v ∂ y Δ y ) = ( ∂ u ∂ x Δ x − ∂ v ∂ x Δ y ) + i ( ∂ v ∂ x Δ x + ∂ u ∂ x Δ y ) = ( ∂ u ∂ x + i ∂ v ∂ x ) ( Δ x + i Δ y ) = ( ∂ u ∂ x + i ∂ v ∂ x ) Δ zΔf=Δu+iΔv=(∂x∂uΔx+∂y∂uΔy)+i(∂x∂vΔx+∂y∂vΔy)=(∂x∂uΔx−∂x∂vΔy)+i(∂x∂vΔx+∂x∂uΔy)=(∂x∂u+i∂x∂v)(Δx+iΔy)=(∂x∂u+i∂x∂v)Δz
于是 f ( z ) f(z) f(z) 在区域 D内可导,为解析函数。且可求得导数
f ′ ( z ) = ∂ u ∂ x + i ∂ v ∂ x = ∂ v ∂ y − i ∂ u ∂ y f'(z)=\frac{∂u}{∂x}+i\frac{∂v}{∂x}= \frac{∂v}{∂y}-i\frac{∂u}{∂y} f′(z)=∂x∂u+i∂x∂v=∂y∂v−i∂y∂u
- 解析函数的像(imag)
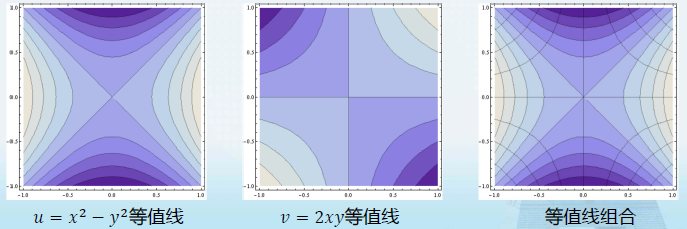
设解析函数为 f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y) 的值域为 G
实部和虚部的等值线分别为 u ( x , y ) = u 0 , v ( x , y ) = v 0 ( u 0 + i v 0 ∈ G ) u(x,y)=u_0,v(x,y)=v_0\quad(u_0+iv_0\in G) u(x,y)=u0,v(x,y)=v0(u0+iv0∈G)
梯度分别为 ∇ u = ∂ u ∂ x i + ∂ u ∂ y j , ∇ v = ∂ v ∂ x i + ∂ v ∂ y j ∇u=\dfrac{∂u}{∂x}\mathbf{i}+\dfrac{∂u}{∂y}\mathbf{j},∇v=\dfrac{∂v}{∂x}\mathbf{i}+\dfrac{∂v}{∂y}\mathbf{j} ∇u=∂x∂ui+∂y∂uj,∇v=∂x∂vi+∂y∂vj
由于 ∇ u ⋅ ∇ v = ∂ u ∂ x ∂ v ∂ x + ∂ u ∂ y ∂ v ∂ y = 0 ∇u\cdot∇v=\dfrac{∂u}{∂x}\dfrac{∂v}{∂x}+\dfrac{∂u}{∂y}\dfrac{∂v}{∂y}=0 ∇u⋅∇v=∂x∂u∂x∂v+∂y∂u∂y∂v=0 ,即实部和虚部的等值线互相垂直。
例如解析函数 w = z 2 w=z^2 w=z2,实部和虚部等值线 u = x 2 − y 2 , v = 2 x y u=x^2-y^2,v=2xy u=x2−y2,v=2xy
初等函数
-
指数函数(Exponential Function):设 z = x + i y z=x+iy z=x+iy
exp ( z ) = e z = e x ( cos y + i sin y ) \exp(z)=e^z=e^x(\cos y+i\sin y) exp(z)=ez=ex(cosy+isiny)
性质:
(1) (加法定理) ∀ z 1 , z 2 ∈ C , e z 1 e z 1 = e z 1 + z 2 ∀ z_1,z_2\in\Complex,e^{z_1}e^{z_1}=e^{z_1+z_2} ∀z1,z2∈C,ez1ez1=ez1+z2
(2) e z e^z ez 在复平面上为解析函数,且有 ( e z ) ′ = e z (e^z)'=e^z (ez)′=ez
(3) 对任意复数 z = x + i y z = x + iy z=x+iy ,有 ∣ e z ∣ = e x , Arg z = y + 2 k π ( k ∈ Z ) |e^z| = e^x ,\text{Arg }z = y + 2kπ ( k\in\Z) ∣ez∣=ex,Arg z=y+2kπ(k∈Z)
(4) e z e^z ez 是只以 2 π i 2πi 2πi 为周期的周期函数
(5) e z 1 = e z 2 ⟺ z 1 − z 2 = 2 k π i ( k ∈ Z ) e^{z_1}=e^{z_2}\iff z_1-z_2=2kπi( k\in\Z) ez1=ez2⟺z1−z2=2kπi(k∈Z)
(6) 欧拉公式(Euler’s Formula): e i y = cos y + i sin y e^{iy}=\cos y+i\sin y eiy=cosy+isiny
指数函数(周期函数)的基本周期区域: B = { z ∣ z ∈ C , 0 < Im z ⩽ 2 π } B=\{z|z\in \Complex,0<\text{Im }z⩽2π\} B={z∣z∈C,0<Im z⩽2π}

-
对数函数(Logarithmic Function): 设 z ≠ 0 z ≠ 0 z=0,称满足 e w = z e^w = z ew=z 的 w w w称为对数函数,记作 w = Ln z w=\text{Ln }z w=Ln z
设 z = r e i θ , w = u + i v z=re^{iθ},w=u+iv z=reiθ,w=u+iv
⟹ e u + i v = r e i θ \implies e^{u+iv}=re^{iθ} ⟹eu+iv=reiθ
⟹ u = ln r = ln ∣ z ∣ , v = Arg z \implies u=\ln r=\ln|z|,v=\text{Arg }z ⟹u=lnr=ln∣z∣,v=Arg z
⟹ w = ln ∣ z ∣ + i Arg z \implies w=\ln|z|+i\text{Arg }z ⟹w=ln∣z∣+iArg z
由于 Arg z = arg z + 2 k π \text{Arg }z=\arg z+2kπ Arg z=argz+2kπ 为多值函数,所以对数函数为多值函数。
上式中每固定一个k就确定一个单值函数,称为 Ln z \text{Ln }z Ln z 的一个单值分支(one-valued branch)。
记 ln z = ln ∣ z ∣ + i arg z \ln z=\ln|z|+i\arg z lnz=ln∣z∣+iargz 为对数主值(principal value),对数函数 Ln z = ln z + 2 k π i , k ∈ Z \text{Ln } z=\ln z+2kπ i,k\in \Z Ln z=lnz+2kπi,k∈Z
性质:
(1) Ln ( z 1 z 2 ) = Ln z 1 + Ln z 2 \text{Ln }(z_1z_2)=\text{Ln }z_1+\text{Ln }z_2 Ln (z1z2)=Ln z1+Ln z2, Ln ( z 1 / z 2 ) = Ln z 1 − Ln z 2 \text{Ln }(z_1/z_2)=\text{Ln }z_1-\text{Ln }z_2 Ln (z1/z2)=Ln z1−Ln z2
等式 Ln z n = n Ln , Ln z n = 1 n Ln z \text{Ln }z^n=n\text{Ln },\text{Ln }\sqrt[n]{z}=\frac{1}{n}\text{Ln }z Ln zn=nLn ,Ln nz=n1Ln z 不再成立
(2) 非零复数的对数有无穷多个值,任何两值之间相差的 2 π i 2π i 2πi 整数倍
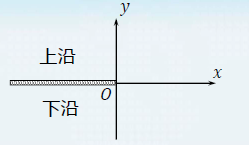
(3) 对于主值 ln z \ln z lnz,除原点和负实轴外 arg z ∈ ( − π , π ) \arg z\in(-π,π) argz∈(−π,π),其他点都是连续的,因为当 x < 0 x<0 x<0, lim y → 0 + arg z = π , lim y → 0 − arg z = − π \lim\limits_{y\to0^+}\arg z=π,\lim\limits_{y\to0^-}\arg z=-π y→0+limargz=π,y→0−limargz=−π
连接原点O及 ∞ ∞ ∞的一条简单连续曲线 K 1 K_1 K1,称为割线(secant),形成相应的割缝区域(Slit area): D 1 = C − K 1 D_1=\Complex-K_1 D1=C−K1。
对数函数在割缝区域 D 1 D_1 D1内的单值连续分支 w k = ln z + 2 k π i w_k=\ln z+2kπ i wk=lnz+2kπi,在区域 D 1 D_1 D1内是解析函数,称为解析分支,其他任何分支都只相差 2 π i 2π i 2πi的整数倍。
(3) 设 w k w_k wk 为对数函数 w = Ln z w=\text{Ln }z w=Ln z 在区域 G内的单值连续分支,则 w k ′ = 1 z , z ∈ G w'_k=\frac{1}{z},z\in G wk′=z1,z∈G
-
幂函数(Power Function):函数 w = z α = e α Ln z w=z^α=e^{α\text{Ln z}} w=zα=eαLn z称为幂函数,其中α为常数, z ≠ 0 z\neq 0 z=0
由于 Ln z \text{Ln z} Ln z 是多值函数,一般 w = z α w=z^α w=zα也是多值函数。
(1) 当 α = n ∈ Z + α=n\in\Z^+ α=n∈Z+时,为复数的n次幂,为单值函数。
w = z n = e n Ln z = e n [ ln ∣ z ∣ + i ( arg z + 2 k π ) ] = ∣ z ∣ n e i n arg z w=z^n=e^{n\text{Ln z}}=e^{n[\ln|z|+i(\arg z+2kπ)]}=|z|^ne^{i n\arg z} w=zn=enLn z=en[ln∣z∣+i(argz+2kπ)]=∣z∣neinargz
(2) 当 α = 1 / n , n ∈ Z + α=1/n,n\in\Z^+ α=1/n,n∈Z+时,为复数的n次方根,为n值函数。
w = z 1 n = e 1 n Ln z = ∣ z ∣ n e i arg z + 2 k π n w=z^{\frac{1}{n}}=e^{\frac{1}{n}\text{Ln z}}=\sqrt[n]{|z|}e^{i\frac{\arg z+2kπ}{n}} w=zn1=en1Ln z=n∣z∣einargz+2kπ
(3) 当 α = 0 , z 0 = e 0 ⋅ Ln z = 1 α=0,z^0=e^{0\cdot \text{Ln z}}=1 α=0,z0=e0⋅Ln z=1
(4) 当α为有理数时,表示为 α = p / q , q > 0 α=p/q,q>0 α=p/q,q>0且p,q为互质的整数
w = z p q = e p q Ln z = ∣ z ∣ p q e i p q ( arg z + 2 k π ) w=z^{\frac{p}{q}}=e^{\frac{p}{q}\text{Ln z}}=|z|^{\frac{p}{q}}e^{i\frac{p}{q}(\arg z+2kπ)} w=zqp=eqpLn z=∣z∣qpeiqp(argz+2kπ)
当 k = 0 , 1 , ⋯ , q − 1 k=0,1,\cdots,q-1 k=0,1,⋯,q−1时,有q 个互异的值。
(5) 若α为无理数或虚数, z α z^α zα为无穷多值
因为 z α = e α Ln z = e α ln z e i 2 α k π z^α=e^{α\text{Ln z}}=e^{α\ln z}e^{i2αkπ} zα=eαLn z=eαlnzei2αkπ,当 k 1 , k 2 ∈ N k_1,k_2\in\N k1,k2∈N且 k 1 ≠ k 2 k_1\neq k_2 k1=k2时, e i 2 α k 1 π ≠ e i 2 α k 2 π e^{i2αk_1π}\neq e^{i2αk_2π} ei2αk1π=ei2αk2π,所以此情形下对应无穷多个值。
性质:在除去原点和负实轴的割缝区域内,幂函数 z α z^α zα是解析的,导数 ( z α ) ′ = α z α − 1 (z^α)'=αz^{α-1} (zα)′=αzα−1 -
三角函数(Trigonometric Function) :由欧拉公式我们可以得到
sin z = 1 2 i ( e i z − e − i z ) , cos z = 1 2 ( e i z + e − i z ) \sin z=\frac{1}{2i}(e^{iz}-e^{-iz}),\cos z=\frac{1}{2}(e^{iz}+e^{-iz}) sinz=2i1(eiz−e−iz),cosz=21(eiz+e−iz)
性质:
(1) sin z , cos z \sin z,\cos z sinz,cosz在复平面解析 ( sin z ) ′ = cos z , ( cos z ) ′ = − sin z (\sin z)'=\cos z,(\cos z)'=-\sin z (sinz)′=cosz,(cosz)′=−sinz
(2) 三角学中实变量的三角函数间的已知公式对复变量的三角函数仍然有效,例如
sin 2 z + cos 2 z = 1 \sin^2 z+\cos^2 z=1 sin2z+cos2z=1
互余性 { sin ( π 2 + z ) = cos z cos ( π 2 + z ) = − sin z{sin(2π+z)=coszcos(2π+z)=−sinz
两角和 { sin ( z 1 ± z 2 ) = sin z 1 cos z 2 ± cos z 1 sin z 2 cos ( z 1 ± z 2 ) = cos z 1 cos z 2 ∓ sin z 1 sin z 2{sin(z1±z2)=sinz1cosz2±cosz1sinz2cos(z1±z2)=cosz1cosz2∓sinz1sinz2
奇偶性 { sin ( − z ) = − sin z cos ( − z ) = cos z{sin(−z)=−sinzcos(−z)=cosz
(3) sin z , cos z \sin z ,\cos z sinz,cosz均以2π为周期
(4) sin z \sin z sinz的零点为 z = k π z=kπ z=kπ, cos z \cos z cosz的零点为 z = ( k + 1 2 ) π z=(k+\frac{1}{2})π z=(k+21)π
(5) sin z , cos z \sin z ,\cos z sinz,cosz均为单值函数
(6) sin z , cos z \sin z ,\cos z sinz,cosz在复数域是无界的
例如 cos i y \cos iy cosiy,当 y → ∞ y\to∞ y→∞时,模 ∣ cos i y ∣ |\cos iy| ∣cosiy∣ 也无限增大
其他三角函数可分别定义为
tan z = sin z cos z , cot z = cos z sin z , sec z = 1 cos z , csc z = 1 sin z \tan z=\dfrac{\sin z}{\cos z},\cot z=\dfrac{\cos z}{\sin z},\sec z=\dfrac{1}{\cos z},\csc z=\dfrac{1}{\sin z} tanz=coszsinz,cotz=sinzcosz,secz=cosz1,cscz=sinz1 -
反三角函数(Inverse Trigonometric Function):反三角函数是三角函数的反函数,定义如下
若 sin w = z \sin w=z sinw=z,则 w = Arccos z w=\text{Arccos }z w=Arccos z为反余弦函数
可求得 Arccos z = − i Ln ( z + z 2 − 1 ) \text{Arccos }z=-i\text{Ln }(z+\sqrt{z^2-1}) Arccos z=−iLn (z+z2−1),可见反余弦为多值函数
同理可定义反正弦函数和反正切函数,且可求得
Arcsin z = − i Ln ( i z + 1 − z 2 ) , Arctan z = i 2 Ln i + z i − z \text{Arcsin }z=-i\text{Ln }(iz+\sqrt{1-z^2}),\quad \text{Arctan }z=\dfrac{i}{2}\text{Ln }\dfrac{i+z}{i-z} Arcsin z=−iLn (iz+1−z2),Arctan z=2iLn i−zi+z -
双曲函数(Hyperbolic function)与反双曲函数
定义 sh z = 1 2 ( e z − e − z ) , ch z = 1 2 ( e z + e − z ) , th z = sh z ch z , cth z = ch z sh z \sh z = \frac{1}{2}(e^z-e^{-z}),\ch z = \frac{1}{2}(e^z+e^{-z}),\th z =\frac{\sh z}{\ch z},\cth z =\frac{\ch z}{\sh z} shz=21(ez−e−z),chz=21(ez+e−z),thz=chzshz,cthz=shzchz
分别称为复变量z 的双曲正弦函数、双曲余弦函数、双曲正切函数及双曲余切函数。
双曲函数与三角函数之间有下列关系:
sh z = − i sin i z , ch z = cos i z , th z = − i tan i z , cth z = i cot i z \sh z = −i\sin iz,\ch z = \cos iz,\th z = −i \tan iz,\cth z = i \cot iz shz=−isiniz,chz=cosiz,thz=−itaniz,cthz=icotiz
由这些关系也可以看出双曲函数是单值的且以虚数2πi 为周期的周期函数. sh z \sh z shz 为奇函数, ch z \ch z chz 为偶函数,而且在复平面内均解析,并有
( sh z ) ′ = ch z , ( ch z ) ′ = sh z (\sh z)′ = \ch z ,(\ch z)'=\sh z (shz)′=chz,(chz)′=shz
由于双曲函数的周期性决定了它们的反函数——反双曲函数的多值性,这里仅将相应的反双曲函数分列如下:
反双曲正弦函数 Arsh z = Ln ( z + z 2 + 1 ) \text{Arsh }z=\text{Ln }(z+\sqrt{z^2+1}) Arsh z=Ln (z+z2+1)
反双曲余弦函数 Arch z = Ln ( z + z 2 − 1 ) \text{Arch }z=\text{Ln }(z+\sqrt{z^2-1}) Arch z=Ln (z+z2−1)
反双曲正切函数 Arth z = 1 2 Ln 1 + z 1 − z \text{Arth }z=\dfrac{1}{2}\text{Ln }\dfrac{1+z}{1-z} Arth z=21Ln 1−z1+z
反双曲余切函数 Arcth z = 1 2 Ln z + 1 z − 1 \text{Arcth }z=\dfrac{1}{2}\text{Ln }\dfrac{z+1}{z-1} Arcth z=21Ln z−1z+1
初等函数的性质
e z 1 e z 1 = e z 1 + z 2 e^{z_1}e^{z_1}=e^{z_1+z_2} ez1ez1=ez1+z2
Ln ( z 1 z 2 ) = Ln z 1 + Ln z 2 Ln ( z 1 / z 2 ) = Ln z 1 − Ln z 2 \text{Ln }(z_1z_2)=\text{Ln }z_1+\text{Ln }z_2 \\ \text{Ln }(z_1/z_2)=\text{Ln }z_1-\text{Ln }z_2 Ln (z1z2)=Ln z1+Ln z2Ln (z1/z2)=Ln z1−Ln z2
sh ( − z ) = − sh z \sh(-z)=-\sh z sh(−z)=−shz
ch ( − z ) = ch z \ch(-z)=\ch z ch(−z)=chz
三角函数 ( sin 2 z + cos 2 z = 1 ) (\sin^2 z+\cos^2 z=1) (sin2z+cos2z=1)
{ sin ( π 2 + z ) = cos z cos ( π 2 + z ) = − sin z
{ sin ( z 1 ± z 2 ) = sin z 1 cos z 2 ± cos z 1 sin z 2 cos ( z 1 ± z 2 ) = cos z 1 cos z 2 ∓ sin z 1 sin z 2
{ sin ( − z ) = − sin z cos ( − z ) = cos z
初等函数导数表
| z = x + i y z=x+\mathrm{i}y z=x+iy | Elementary Function | Derivative |
|---|---|---|
| 指数函数 | e z = e x ( cos y + i sin y ) e^z=e^x(\cos y+\mathrm{i}\sin y) ez=ex(cosy+isiny) ( T = 2 π i ) (T=2π\mathrm{i}) (T=2πi) | ( e z ) ′ = e z (e^z)'=e^z (ez)′=ez |
| 对数函数 | Ln z = ln z + 2 k π i \text{Ln } z=\ln z+2kπ\mathrm{i} Ln z=lnz+2kπi ln z = ln ∣ z ∣ + i arg z \ln z=\ln\mid z\mid+i\arg z lnz=ln∣z∣+iargz | ( ln z ) ′ = 1 z (\ln z)'=\dfrac{1}{z} (lnz)′=z1 |
| 幂函数 | z α = e α Ln z z^α=e^{α\text{Ln z}} zα=eαLn z ( z ≠ 0 ) (z\neq 0) (z=0) | ( z α ) ′ = α z α − 1 (z^α)'=αz^{α-1} (zα)′=αzα−1 ( z ∉ R − ) (z\not\in\R^-) (z∈R−) |
| 三角函数 ( T = 2 π ) (T=2π) (T=2π) | sin z = 1 2 i ( e i z − e − i z ) \sin z=\frac{1}{2\mathrm{i}}(e^{\mathrm{i}z}-e^{-\mathrm{i}z}) sinz=2i1(eiz−e−iz) cos z = 1 2 ( e i z + e − i z ) \cos z=\frac{1}{2}(e^{\mathrm{i}z}+e^{-\mathrm{i}z}) cosz=21(eiz+e−iz) | ( sin z ) ′ = cos z (\sin z)'=\cos z (sinz)′=cosz ( cos z ) ′ = − sin z (\cos z)'=-\sin z (cosz)′=−sinz |
| 反三角函数 | Arccos z = − i Ln ( z + z 2 − 1 ) \text{Arccos }z=-\mathrm{i}\text{Ln }(z+\sqrt{z^2-1}) Arccos z=−iLn (z+z2−1) Arcsin z = − i Ln ( i z + 1 − z 2 ) \text{Arcsin }z=-\mathrm{i}\text{Ln }(\mathrm{i}z+\sqrt{1-z^2}) Arcsin z=−iLn (iz+1−z2) | |
| 双曲函数 ( T = 2 π i ) (T=2π\mathrm{i}) (T=2πi) | sh z = 1 2 ( e z − e − z ) = − i sin i z \sh z = \frac{1}{2}(e^z-e^{-z})=−\mathrm{i}\sin \mathrm{i}z shz=21(ez−e−z)=−isiniz ch z = 1 2 ( e z + e − z ) = cos i z \ch z = \frac{1}{2}(e^z+e^{-z})=\cos \mathrm{i}z chz=21(ez+e−z)=cosiz | ( sh z ) ′ = ch z (\sh z)'= \ch z (shz)′=chz ( ch z ) ′ = sh z (\ch z)'=\sh z (chz)′=shz |
| 反双曲函数 | Arsh z = Ln ( z + z 2 + 1 ) \text{Arsh }z=\text{Ln }(z+\sqrt{z^2+1}) Arsh z=Ln (z+z2+1) Arch z = Ln ( z + z 2 − 1 ) \text{Arch }z=\text{Ln }(z+\sqrt{z^2-1}) Arch z=Ln (z+z2−1) |
复变函数的积分
积分的概念
-
复变函数积分定义:设C 为一条起点在a ,终点在b 的有向光滑曲线(或逐段光滑曲线),其方程为 w = f ( z ) w=f(z) w=f(z)。
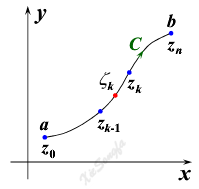
(1) 将曲线 C任意分为n个小弧段,分点为 a = z 0 , z 1 , ⋯ , z k − 1 , z k , ⋯ , z n = b a=z_0,z_1,\cdots,z_{k-1},z_k,\cdots,z_n=b a=z0,z1,⋯,zk−1,zk,⋯,zn=b,令 Δ z k = z k − z k − 1 , λ = max ∣ Δ z k ∣ Δz_k=z_k-z_{k-1},λ=\max|Δz_k| Δzk=zk−zk−1,λ=max∣Δzk∣
(2) 在每个小弧段 z k − 1 z k ⏠ \overgroup{z_{k-1}z_k} zk−1zk 上任取一点 ζ k ζ_k ζk,作和 S n = ∑ k = 1 n f ( ζ k ) Δ z k S_n=\displaystyle\sum_{k=1}^{n}f(ζ_k)Δz_k Sn=k=1∑nf(ζk)Δzk
若极限 lim λ → 0 S n \lim\limits_{λ\to0}S_n λ→0limSn 存在,且不依赖于C的划分和 ζ k ζ_k ζk的取法,则称此极限为 f ( z ) f(z) f(z) 沿曲线 C从a到b的积分,记作 ∫ C f ( z ) d z = lim λ → 0 ∑ k = 1 n f ( ζ k ) Δ z k \displaystyle\int_{C}f(z)dz=\lim\limits_{λ\to0}\sum_{k=1}^{n}f(ζ_k)Δz_k ∫Cf(z)dz=λ→0limk=1∑nf(ζk)Δzk
注:C负方向的积分记作 ∫ C − f ( z ) d z \displaystyle\int_{C^-}f(z)dz ∫C−f(z)dz,若C为闭曲线,积分记作 ∮ C f ( z ) d z \displaystyle\oint_{C}f(z)dz ∮Cf(z)dz(C的正向为逆时针方向) -
积分的计算:
(1) 设 f ( z ) = u ( x , y ) + i v ( x , y ) f(z)=u(x,y)+\text{i }v(x,y) f(z)=u(x,y)+i v(x,y),可求得 ∫ C f ( z ) d z = ∫ C u d x − v d y + i ∫ C v d x + u d y \displaystyle\int_{C}f(z)dz=\int_{C}udx-vdy+i\int_{C}vdx+udy ∫Cf(z)dz=∫Cudx−vdy+i∫Cvdx+udy上述公式可看做 f ( z ) = u + i v f(z)=u+iv f(z)=u+iv与 d z = d x + i d y dz=dx+idy dz=dx+idy形式相乘的结果
(2) 还可化为普通的定积分,设曲线C的参数方程为 z ( t ) = x ( t ) + i y ( t ) ( α ⩽ t ⩽ β ) z(t)=x(t)+iy(t)\quad(α⩽t⩽β) z(t)=x(t)+iy(t)(α⩽t⩽β),带入可得
∫ C f ( z ) d z = ∫ α β f [ z ( t ) ] z ′ ( t ) d t \displaystyle\int_{C}f(z)dz=\int_{α}^{β}f[z(t)]z'(t)dt ∫Cf(z)dz=∫αβf[z(t)]z′(t)dt -
复积分的基本性质:设 f ( z ) , g ( z ) f(z),g(z) f(z),g(z)在简单曲线上连续
(1) ∫ C k f ( z ) d z = k ∫ C f ( z ) d z ( k 为 复 常 数 ) \displaystyle\int_{C}kf(z)dz=k\int_{C}f(z)dz\quad(k为复常数) ∫Ckf(z)dz=k∫Cf(z)dz(k为复常数)
(2) ∫ C [ f ( z ) ± g ( z ) ] d z = ∫ C f ( z ) d z ± ∫ C g ( z ) d z \displaystyle\int_{C}[f(z)± g(z)]dz=\int_{C}f(z)dz± \int_{C}g(z)dz ∫C[f(z)±g(z)]dz=∫Cf(z)dz±∫Cg(z)dz
(3) ∫ C f ( z ) d z = − ∫ C − f ( z ) d z \displaystyle\int_{C}f(z)dz=-\int_{C^-}f(z)dz ∫Cf(z)dz=−∫C−f(z)dz
(4) 设 C由光滑曲线 C 1 , C 2 C_1,C_2 C1,C2 分段连接而成
∫ C f ( z ) d z = ∫ C 1 f ( z ) d z + ∫ C 2 f ( z ) d z \displaystyle\int_{C}f(z)dz=\int_{C_1}f(z)dz+\int_{C_2}f(z)dz ∫Cf(z)dz=∫C1f(z)dz+∫C2f(z)dz
(5) ∣ ∫ C f ( z ) d z ∣ ⩽ ∫ C ∣ f ( z ) ∣ d s \displaystyle|\int_{C}f(z)dz|⩽\int_{C}|f(z)|ds ∣∫Cf(z)dz∣⩽∫C∣f(z)∣ds
特别的,若在C 上有 ∣ f ( z ) ∣ ⩽ M |f(z)|⩽M ∣f(z)∣⩽M,C的长为L,则 ∣ ∫ C f ( z ) d z ∣ ⩽ M L \displaystyle|\int_{C}f(z)dz|⩽ML ∣∫Cf(z)dz∣⩽ML
该不等式称为积分估值不等式,提供了一种估计复变函数积分的模的方法 -
复积分实例:
(1) 设C为连接 a,b 两点的简单曲线,则有
设曲线C的参数方程为 z ( t ) = x ( t ) + i y ( t ) ( α ⩽ t ⩽ β ) z(t)=x(t)+iy(t)\quad(α⩽t⩽β) z(t)=x(t)+iy(t)(α⩽t⩽β)
∫ C d z = ∫ α β z ′ ( t ) d t = z ( t ) ∣ α β = b − a \displaystyle\int_{C}dz=\int_{α}^{β}z'(t)dt=z(t)|_{α}^{β}=b-a ∫Cdz=∫αβz′(t)dt=z(t)∣αβ=b−a
∫ C z d z = ∫ C x d x − y d y + i ∫ C y d x + x d y = 1 2 ( b 2 − a 2 ) \displaystyle\int_{C}zdz=\int_{C}xdx-ydy+i\int_{C}ydx+xdy=\frac{1}{2}(b^2-a^2) ∫Czdz=∫Cxdx−ydy+i∫Cydx+xdy=21(b2−a2)
特别,若为简单闭曲线,则上述积分等于零。
此例揭示了一个很好的性质,函数 f ( z ) = 1 , f ( z ) = z f(z)=1,f(z)=z f(z)=1,f(z)=z在曲线C的积分只依赖于C起点与终点,而与C 的形状无关
(2) 设曲线C是以a为圆心,r为半径的正向圆周
∮ C 1 ( z − a ) n d z = { 2 π i , n = 1 0 , n ≠ 1 , n ∈ Z \displaystyle\oint_{C}\dfrac{1}{(z-a)^n}dz=∮C(z−a)n1dz={2πi,0,n=1n=1,n∈Z
设C 的参数方程为 z = a + r e i θ ( 0 ⩽ θ ⩽ 2 π ) z=a+re^{iθ}\quad(0⩽θ⩽2π) z=a+reiθ(0⩽θ⩽2π)则
∮ C 1 ( z − a ) n d z = ∫ 0 2 π i r e i θ r n e i n θ d θ = i r n − 1 ∫ 0 2 π e − i ( n − 1 ) θ d θ \displaystyle\oint_{C}\dfrac{1}{(z-a)^n}dz=\int_{0}^{2π}\dfrac{ire^{iθ}}{r^ne^{inθ}}dθ=\dfrac{i}{r^{n-1}}\int_{0}^{2π}e^{-i(n-1)θ}dθ ∮C(z−a)n1dz=∫02πrneinθireiθdθ=rn−1i∫02πe−i(n−1)θdθ
柯西积分定理(Cauchy Integral Theorem)
通过上节的例子可以发现,有的函数的积分只依赖于积分路径的起点与终点,而与积分路径的形状无关,而有的函数,其积分不仅与积分路径的起点与终点有关,而且与积分路径的形状也有关。深入观察后,可知,前一类函数是解析函数。
-
柯西积分定理 或称 柯西-古萨定理(Cauchy-Goursat Theorem)
如果函数 f ( z ) f(z) f(z)在单连通区域D内解析,则 f ( z ) f(z) f(z)在D内沿任一简单闭曲线 Γ Γ Γ积分 ∮ Γ f ( z ) d z = 0 \displaystyle\oint_{Γ}f(z)dz=0 ∮Γf(z)dz=0
证: ∮ Γ f ( z ) d z = ∮ Γ u d x − v d y + i ∮ Γ v d x + u d y = formula Green − ∬ G ( ∂ v ∂ x + ∂ u ∂ y ) + i ∬ G ( ∂ u ∂ x − ∂ v ∂ y ) = C-R 0∮Γf(z)dz=∮Γudx−vdy+i∮Γvdx+udyGreenformula−∬G(∂x∂v+∂y∂u)+i∬G(∂x∂u−∂y∂v)C-R0
扩展如果C是单连通区域D的边界, f ( z ) f(z) f(z)在D内解析,在 D ˉ = D ∪ C \bar D=D\cup C Dˉ=D∪C上连续,定理依旧成立。 -
复合闭路定理——多连通区域上的柯西定理
设有 n + 1 n+1 n+1条简单闭曲线 C 0 , C 1 , ⋯ , C n C_0,C_1,\cdots,C_n C0,C1,⋯,Cn,其中 C 1 , ⋯ , C n C_1,\cdots,C_n C1,⋯,Cn均在 C 0 C_0 C0的内区域内,而且它们既不包含也不想交。 C 0 C_0 C0内部与 C 1 , ⋯ , C n C_1,\cdots,C_n C1,⋯,Cn外部围成多连通区域D, 称D的边界 C = C 0 + C 1 − + ⋯ + C n − C=C_0+C_1^-+\cdots+C_n^- C=C0+C1−+⋯+Cn−为复合闭路(Compound closed path)。在外边界 C 0 C_0 C0,C的正向为逆时针方向,在内边界上,C的正向为顺时针方向。
D与其边界构成闭区域 D ˉ \bar D Dˉ,设 f ( z ) f(z) f(z)在 D ˉ \bar D Dˉ上解析,则 ∮ C f ( z ) d z = 0 \displaystyle\oint_{C}f(z)dz=0 ∮Cf(z)dz=0 或 ∮ C 0 f ( z ) d z = ∑ k = 1 n ∮ C k f ( z ) d z \displaystyle\oint_{C_0}f(z)dz=\sum_{k=1}^{n}\oint_{C_k}f(z)dz ∮C0f(z)dz=k=1∑n∮Ckf(z)dz
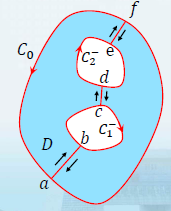
证明:以上图为例,在 C 0 C_0 C0内做简单光滑弧 a b ⌢ , c d ⌢ , e f ⌢ \overset{\frown}{ab} ,\overset{\frown}{cd} ,\overset{\frown}{ef} ab⌢,cd⌢,ef⌢ 连接 C 0 , C 1 , C 2 C_0,C_1,C_2 C0,C1,C2,将D分成两个简单单连通区域 D 1 , D 2 D_1,D_2 D1,D2,边界分别记作 L 1 , L 2 L_1,L_2 L1,L2,由于 f ( z ) f(z) f(z)在 D ˉ \bar D Dˉ上解析,根据柯西积分定理有 ∮ L 1 f ( z ) d z = 0 , ∮ L 2 f ( z ) d z = 0 \displaystyle\oint_{L_1}f(z)dz=0,\oint_{L_2}f(z)dz=0 ∮L1f(z)dz=0,∮L2f(z)dz=0
将两式相加 ∮ L 1 f ( z ) d z + ∮ L 2 f ( z ) d z = 0 \displaystyle\oint_{L_1}f(z)dz+\oint_{L_2}f(z)dz=0 ∮L1f(z)dz+∮L2f(z)dz=0,由于在连接弧上的积分方向相反,刚好相互抵消,即 ∮ C 0 + C 1 − + C 2 − f ( z ) d z = ∮ C f ( z ) d z = 0 \displaystyle\oint_{C_0+C_1^-+C_2^-}f(z)dz=\oint_{C}f(z)dz=0 ∮C0+C1−+C2−f(z)dz=∮Cf(z)dz=0
( ⋆ \star ⋆) 从定理的证明过程中,可知,在区域内的一个解析函数沿闭曲线的积分,不因闭曲线在区域内做连续变形而改变它的值,只要在变形过程中曲线不经过函数的奇点就行。这一个重要的事实,称为闭路变形原理。 -
挖奇点法:设C为包含a的简单闭曲线,则
∮ C 1 ( z − a ) n d z = { 2 π i , n = 1 0 , n ≠ 1 , n ∈ Z \displaystyle\oint_{C}\dfrac{1}{(z-a)^n}dz=∮C(z−a)n1dz={2πi,0,n=1n=1,n∈Z
C内只包含奇点a,做以a为圆心,r为半径的正向圆周 Γ Γ Γ,由复合闭路定理知 ∮ C 1 ( z − a ) n d z = ∮ Γ 1 ( z − a ) n d z \displaystyle\oint_{C}\dfrac{1}{(z-a)^n}dz=\oint_{Γ}\dfrac{1}{(z-a)^n}dz ∮C(z−a)n1dz=∮Γ(z−a)n1dz,根据上节的实例证明可得上式。 -
原函数(Primitive Function)
柯西积分定理 - 推论若 z 0 , z 1 z_0,z_1 z0,z1单连通区域D内任意两点, C 1 , C 2 ⊂ D C_1,C_2\sub D C1,C2⊂D为连接 z 0 , z 1 z_0,z_1 z0,z1 的任意两条曲线,则 ∫ C 1 f ( z ) d z = ∫ C 2 f ( z ) d z \displaystyle\int_{C_1}f(z)dz=\int_{C_2}f(z)dz ∫C1f(z)dz=∫C2f(z)dz
可知,解析函数积分与路径无关,仅由起点和终点来确定,即
∫ C f ( ξ ) d ξ = ∫ z 0 z 1 f ( ξ ) d ξ \displaystyle\int_{C}f(ξ)dξ=\int_{z_0}^{z_1}f(ξ)dξ ∫Cf(ξ)dξ=∫z0z1f(ξ)dξ,这里 z 0 , z 1 z_0,z_1 z0,z1分别称为积分的上限和下限。
当下限 z 0 z_0 z0固定,让上限 z 1 = z z_1=z z1=z在D内变动,则积分 ∫ z 0 ξ f ( ξ ) d z \displaystyle\int_{z_0}^{ξ}f(ξ)dz ∫z0ξf(ξ)dz在D内确定了一个单值函数 F ( z ) = ∫ z 0 z f ( ξ ) d ξ F(z)=\displaystyle\int_{z_0}^{z}f(ξ)dξ F(z)=∫z0zf(ξ)dξ,对这个函数我们有
定理 1:设 f ( z ) f(z) f(z)在单连通区域D内解析, 则函数 F ( z ) F(z) F(z) 在区域内一定是解析函数,且 F ′ ( z ) = f ( z ) F'(z)=f(z) F′(z)=f(z)
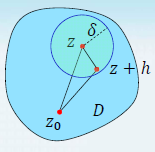
证明:设z为D内任意一点,在D内以 δ δ δ为半径,z为圆心作圆,在圆内取点 z + h z+h z+h,则有
F ( z + h ) − F ( z ) = ∫ z 0 z + h f ( ξ ) d ξ − ∫ z 0 z f ( ξ ) d ξ = ∫ z z + h f ( ξ ) d ξ F(z+h)-F(z)=\displaystyle\int_{z_0}^{z+h}f(ξ)dξ-\int_{z_0}^{z}f(ξ)dξ=\int_{z}^{z+h}f(ξ)dξ F(z+h)−F(z)=∫z0z+hf(ξ)dξ−∫z0zf(ξ)dξ=∫zz+hf(ξ)dξ
上式取 z z z到 z + h z+h z+h的直线段积分,则有
F ( z + h ) − F ( z ) h − f ( z ) = 1 h ∫ z z + h [ f ( ξ ) − f ( z ) ] d ξ \displaystyle\dfrac{F(z+h)-F(z)}{h}-f(z)=\dfrac{1}{h}\int_{z}^{z+h}[f(ξ)-f(z)]dξ hF(z+h)−F(z)−f(z)=h1∫zz+h[f(ξ)−f(z)]dξ
因为 f ( z ) f(z) f(z)在D内解析,所以 f ( z ) f(z) f(z)在D得连续
∀ ϵ > 0 , ∃ δ > 0 ∀ϵ>0,\exists δ>0 ∀ϵ>0,∃δ>0,使得 ∣ ξ − z ∣ < δ |ξ-z|<δ ∣ξ−z∣<δ在圆内恒成立,即当 ∣ h ∣ < δ |h|<δ ∣h∣<δ时,总有 ∣ f ( ξ ) − f ( z ) ∣ < ϵ |f(ξ)-f(z)|<ϵ ∣f(ξ)−f(z)∣<ϵ。根据积分估值不等式,有
∣ F ( z + h ) − F ( z ) h − f ( z ) ∣ = 1 ∣ h ∣ ∣ ∫ z z + h [ f ( ξ ) − f ( z ) ] d ξ ∣ ⩽ 1 ∣ h ∣ ∫ z z + h ∣ f ( ξ ) − f ( z ) ∣ d s < 1 ∣ h ∣ ⋅ ϵ ⋅ ∣ h ∣ = ϵ∣hF(z+h)−F(z)−f(z)∣=∣h∣1∣∣∣∣∣∫zz+h[f(ξ)−f(z)]dξ∣∣∣∣∣⩽∣h∣1∫zz+h∣f(ξ)−f(z)∣ds<∣h∣1⋅ϵ⋅∣h∣=ϵ
这说明 lim h → 0 F ( z + h ) − F ( z ) h = f ( z ) \lim\limits_{h\to0}\dfrac{F(z+h)-F(z)}{h}=f(z) h→0limhF(z+h)−F(z)=f(z),即 F ′ ( z ) = f ( z ) F'(z)=f(z) F′(z)=f(z)
原函数:在单连通区域D内称满足条件 F ′ ( z ) = f ( z ) F'(z)=f(z) F′(z)=f(z)的称 F ( z ) F(z) F(z)为区域D内 f ( z ) f(z) f(z)的一个原函数(Primitive Function)。称 f ( z ) f(z) f(z)的原函数的全体为 f ( z ) f(z) f(z) 的不定积分,记为 ∫ f ( z ) d z \displaystyle\int f(z)dz ∫f(z)dz。
若 Φ ( z ) , F ( z ) Φ(z),F(z) Φ(z),F(z)同为 f ( z ) f(z) f(z)在区域D的原函数,则 [ Φ ( z ) − F ( z ) ] ′ = f ( z ) − f ( z ) = 0 [Φ(z)-F(z)]'=f(z)-f(z)=0 [Φ(z)−F(z)]′=f(z)−f(z)=0,于是 Φ ( z ) − F ( z ) ≡ C Φ(z)-F(z)\equiv C Φ(z)−F(z)≡C,其中C为任意常数。因此,解析函数存在无穷多个原函数,且任意两个原函数之间只相差一个常数。不定积分为 ∫ f ( z ) d z = Φ ( z ) + C \displaystyle\int f(z)dz=Φ(z)+C ∫f(z)dz=Φ(z)+C
定理 2:设 f ( z ) f(z) f(z)在单连通区域D内解析, F ( z ) F(z) F(z) 为 f ( z ) f(z) f(z)的一个原函数,对于D内任意两点 z 0 , z 1 z_0,z_1 z0,z1 牛顿-莱布尼茨公式依旧成立,即 ∫ z 0 z 1 f ( z ) d z = F ( z 1 ) − F ( z 0 ) \displaystyle\int_{z_0}^{z_1}f(z)dz=F(z_1)-F(z_0) ∫z0z1f(z)dz=F(z1)−F(z0) -
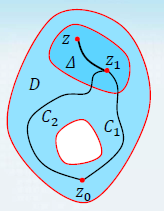
多连通区域上解析函数的原函数:设 f ( z ) f(z) f(z)在多连通区域D内解析,定义 F ( z ) = ∫ z 0 z f ( ξ ) d ξ F(z)=\displaystyle\int_{z_0}^{z}f(ξ)dξ F(z)=∫z0zf(ξ)dξ ,此函数可能为多值函数。
在D内取一单连通区域 Δ Δ Δ, 定点 z 0 , z 1 ∈ Δ z_0,z_1\in Δ z0,z1∈Δ, C 1 C_1 C1为D内从 z 0 z_0 z0到 z 1 z_1 z1的一条固定的简单曲线,定义 F 0 ( z ) = ∫ C 1 f ( ξ ) d ξ + ∫ z 1 z ⌢ f ( ξ ) d ξ F_0(z)=\displaystyle\int_{C_1}f(ξ)dξ+\int_{\overset{\frown}{z_1z}}f(ξ)dξ F0(z)=∫C1f(ξ)dξ+∫z1z⌢f(ξ)dξ
则 F 0 ( z ) F_0(z) F0(z)为 F ( z ) F(z) F(z)在 Δ Δ Δ内的一个解析分支
柯西积分公式(Cauchy Integral Formula)
-
引述:设 f ( z ) f(z) f(z)在单连通区域D内解析,则函数 f ( z ) z − z 0 \dfrac{f(z)}{z-z_0} z−z0f(z)在 z 0 z_0 z0处不解析。C为D内围绕 z 0 z_0 z0的闭曲线,所以积分 ∮ C f ( z ) z − z 0 d z \displaystyle\oint_C \dfrac{f(z)}{z-z_0}dz ∮Cz−z0f(z)dz一般不为零。
以 z 0 z_0 z0为中心, ρ > 0 ρ>0 ρ>0为半径的正向圆周为积分曲线 C ρ C_ρ Cρ,根据复合闭路定理, ∮ C f ( z ) z − z 0 d z = ∮ C ρ f ( z ) z − z 0 d z \displaystyle \oint_C \dfrac{f(z)}{z-z_0}dz= \oint_{C_ρ} \dfrac{f(z)}{z-z_0}dz ∮Cz−z0f(z)dz=∮Cρz−z0f(z)dz
由于 f ( z ) f(z) f(z)的连续性, f ( z ) → f ( z 0 ) ( ρ → 0 ) f(z)\to f(z_0)\quad(ρ\to 0) f(z)→f(z0)(ρ→0),因而可以猜想,积分
∮ C f ( z ) z − z 0 d z → f ( z 0 ) ∮ C ρ 1 z − z 0 d z = 2 π i f ( z 0 ) ( ρ → 0 ) \displaystyle \oint_{C} \dfrac{f(z)}{z-z_0}dz\to f(z_0)\oint_{C_ρ} \dfrac{1}{z-z_0}dz=2πi f(z_0) \quad(ρ\to 0) ∮Cz−z0f(z)dz→f(z0)∮Cρz−z01dz=2πif(z0)(ρ→0)
当然,证明过程是复杂的,我们得到如下定理。 -
柯西积分公式:设区域D是以C为边界的单连通区域,函数 f ( z ) f(z) f(z)在区域D内解析,在 D ˉ \bar D Dˉ连续, z 0 z_0 z0是D内的任意一点则: f ( z 0 ) = 1 2 π i ∮ C f ( z ) z − z 0 d z \displaystyle f(z_0)=\dfrac {1}{2π \text{i}}\oint_C \dfrac{f(z)}{z-z_0}dz f(z0)=2πi1∮Cz−z0f(z)dz 柯西积分公式对于有 n + 1 n+1 n+1条简单闭曲线组成的复合闭路 C = C 0 + C 1 − + ⋯ + C n − C=C_0+C_1^-+\cdots+C_n^- C=C0+C1−+⋯+Cn−围成的多连通区域D 仍然有效。
通过这个公式可以把函数 f ( z ) f(z) f(z)在解析域内任意点的值用他在边界上的积分来表示,这是解析函数的又一特征。
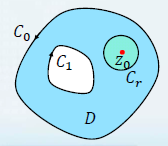
推论 1 (平均值公式):设 f ( z ) f(z) f(z) 在圆盘 ∣ z − z 0 ∣ < ρ |z-z_0|<ρ ∣z−z0∣<ρ 上解析,在 ∣ z − z 0 ∣ ⩽ ρ |z-z_0|⩽ ρ ∣z−z0∣⩽ρ 上连续,则 f ( z 0 ) = 1 2 π ∫ 0 2 π f ( z 0 + ρ e i θ ) d θ \displaystyle f(z_0)=\dfrac {1}{2π}\int_{0}^{2\pi} f(z_0+ρe^{iθ})dθ f(z0)=2π1∫02πf(z0+ρeiθ)dθ
推论 2:设区域D由同心圆周 K 1 , K 2 ( K 2 K_1,K_2(K_2 K1,K2(K2包含于 K 1 ) K_1) K1) 所围成的圆环,多连通区域D的边界 Γ = K 1 + K 2 − Γ=K_1+K_2^- Γ=K1+K2−,函数 f ( z ) f(z) f(z) 在圆环D内解析,在 D ˉ \bar D Dˉ连续, z 0 z_0 z0为D内任意一点,则 f ( z 0 ) = 1 2 π i ∮ Γ f ( z ) z − z 0 d z \displaystyle f(z_0)=\dfrac {1}{2π i}\oint_Γ \dfrac{f(z)}{z-z_0}dz f(z0)=2πi1∮Γz−z0f(z)dz -
柯西积分公式的应用
高阶导数公式:解析函数的导数仍然为解析函数,它的n阶导数为
f ( n ) ( z 0 ) = n ! 2 π i ∮ C f ( z ) ( z − z 0 ) n + 1 d z ( n ∈ Z + ) \displaystyle f^{(n)}(z_0)=\frac {n!}{2\pi i}\oint_C \frac{f(z)}{(z-z_0)^{n+1}}dz \quad(n\in\Z^+) f(n)(z0)=2πin!∮C(z−z0)n+1f(z)dz(n∈Z+)其中C为函数 f ( z ) f(z) f(z)的解析域内围绕 z 0 z_0 z0的任意一条简单闭曲线。
可用数学归纳法证明上式。此性质常称为解析函数的无穷可微性。
柯西不等式:设 f ( z ) f(z) f(z) 在圆周 C : ∣ z − z 0 ∣ = ρ 0 ( ρ 0 > 0 ) C:|z-z_0|=ρ_0(ρ_0>0) C:∣z−z0∣=ρ0(ρ0>0) 所围成的区域内解析,在 ∣ z − z 0 ∣ ⩽ ρ 0 |z-z_0|⩽ ρ_0 ∣z−z0∣⩽ρ0 上连续, M ( ρ ) = max ∣ z − z 0 ∣ = ρ ∣ f ( z ) ∣ ( 0 < ρ ⩽ ρ 0 ) \displaystyle M(ρ)=\max_{|z-z_0|=ρ}|f(z)|\quad (0<ρ⩽ρ_0) M(ρ)=∣z−z0∣=ρmax∣f(z)∣(0<ρ⩽ρ0),则 f ( n ) ( z 0 ) n ! ⩽ M ( ρ ) ρ n ( n ∈ Z + ) \dfrac {f^{(n)}(z_0)}{n!}⩽\dfrac{M(ρ)}{ρ^n}\quad(n\in\Z^+) n!f(n)(z0)⩽ρnM(ρ)(n∈Z+)
最大模原理:设 f ( z ) f(z) f(z) 在闭区域 D ˉ \bar D Dˉ上解析,则 ∣ f ( z ) ∣ |f(z)| ∣f(z)∣只能在边界 ∂ D ∂D ∂D上取得极大值。
刘维尔(Liouville)定理:设函数 f ( z ) f(z) f(z)在整个复平面上的解析且有界,则 f ( z ) f(z) f(z)为一常数。
证明:设存在常数 M > 0 M>0 M>0 使得 ∣ f ( z ) ∣ ⩽ M |f(z)|⩽M ∣f(z)∣⩽M,对于任意 z 0 ∈ C z_0\in\Complex z0∈C及任意的 ρ > 0 ρ>0 ρ>0, 有
∣ f ′ ( z 0 ) ∣ ⩽ M ( ρ ) ρ ⩽ M ρ → 0 ( ρ → + ∞ ) |f'(z_0)|⩽\dfrac{M(ρ)}{ρ}⩽\dfrac{M}{ρ}\to 0\quad(ρ\to+\infty) ∣f′(z0)∣⩽ρM(ρ)⩽ρM→0(ρ→+∞)
因此 ∀ z 0 ∈ C , f ′ ( z 0 ) = 0 \forall z_0\in\Complex,f'(z_0)=0 ∀z0∈C,f′(z0)=0,所以 f ( z ) f(z) f(z)在复平面上为常数。
调和函数(Harmonic Function)
定义:设二元实函数 φ ( x , y ) φ(x, y) φ(x,y)在定义域D内有二阶连续偏导数,且满足二维拉普拉斯(Laplace)方程 Δ φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 = 0 Δφ=\dfrac{∂^2φ}{∂x^2}+\dfrac{∂^2φ}{∂y^2}=0 Δφ=∂x2∂2φ+∂y2∂2φ=0 则称 φ ( x , y ) φ(x, y) φ(x,y)为D内的调和函数(harmonic function)。也记为 Δ φ = φ x x + φ y y = 0 Δφ=φ_{xx}+φ_{yy}=0 Δφ=φxx+φyy=0
定理 1:设 f ( z ) = u ( x , y ) + i v ( x , y ) f (z)=u(x,y)+iv(x,y) f(z)=u(x,y)+iv(x,y)在区域D内解析,则实部 u ( x , y ) u(x,y) u(x,y)与虚部 u ( x , y ) u(x,y) u(x,y) 均为D内的调和函数。
证明:由于解析函数有任意阶导数, 所以 u , v u,v u,v在区域D内有任意阶连续偏导数.。由C-R条件 u x = v y , u y = − v x u_x=v_y,u_y=-v_x ux=vy,uy=−vx 有 u x x = v y x , u y y = − v x y u_{xx}=v_{yx},u_{yy}=-v_{xy} uxx=vyx,uyy=−vxy,由此得 Δ u = u x x + u y y = 0 Δu=u_{xx}+u_{yy}=0 Δu=uxx+uyy=0,同理可得 Δ v = 0 Δv=0 Δv=0
定义:若区域D内的调和函数 u ( x , y ) , v ( x , y ) u(x,y),v(x,y) u(x,y),v(x,y)满足C-R条件 u x = v y , u y = − v x u_x=v_y,u_y=-v_x ux=vy,uy=−vx,则称 u ( x , y ) , v ( x , y ) u(x,y),v(x,y) u(x,y),v(x,y)为区域D的共轭调和函数(conjugate harmonic function)。
应用:构造解析函数 f ( z ) = u + i v f (z) = u + iv f(z)=u+iv
(1) 由于共轭调和函数的关系,已知其中一个函数,根据C-R条件便可确定另一个,这种方法称为偏积分法。
设已知 u ( x , y ) u(x,y) u(x,y),则有 d v = v x d x + v y d y = − u y d x + u x d y dv=v_xdx+v_ydy=-u_ydx+u_xdy dv=vxdx+vydy=−uydx+uxdy,由此有
v ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) − u y d x + u x d y + C = ∫ x 0 x − u y d x + ∫ y 0 y u x d y + C \displaystyle v(x,y)=\int_{(x_0,y_0)}^{(x,y)}-u_ydx+u_xdy+C=\int_{x_0}^{x}-u_ydx+\int_{y_0}^{y}u_xdy+C v(x,y)=∫(x0,y0)(x,y)−uydx+uxdy+C=∫x0x−uydx+∫y0yuxdy+C
其中 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)为定点,C为常数。
(2) 设已知 u ( x , y ) u(x,y) u(x,y),由于要求 f ( z ) = u + i v f (z) = u + iv f(z)=u+iv为解析函数,所以有
f ′ ( z ) = u x + i v x = u x − i u y f'(z)=u_x+iv_x=u_x-iu_y f′(z)=ux+ivx=ux−iuy,于是求 f ′ ( z ) f'(z) f′(z)的原函数即可。这种方法称为原函数法。
二元函数全微分:若函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)的全增量 Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) Δ z=f(x+Δ x,y+Δ y)-f(x,y) Δz=f(x+Δx,y+Δy)−f(x,y)可表示为 Δ z = A Δ x + B Δ y + o ( ρ ) Δ z=AΔ x+BΔ y+o(ρ) Δz=AΔx+BΔy+o(ρ)其中A和B不依赖于 Δ x 和 Δ y Δ x和Δ y Δx和Δy而仅与x,y有关, ρ = ( Δ x ) 2 + ( Δ y ) 2 ρ=\sqrt{(Δ x)^2+(Δ y)^2} ρ=(Δx)2+(Δy)2,则称函数在点 ( x , y ) (x,y) (x,y)可微分, A Δ x + B Δ y AΔ x+BΔ y AΔx+BΔy叫做全微分,记作 d z \mathrm{d}z dz,即 d z = A Δ x + B Δ y \mathrm{d}z=AΔ x+BΔ y dz=AΔx+BΔy
必要条件 函 数 z = f ( x , y ) 在 ( x , y ) 可 微 分 , 那 该 函 数 在 ( x , y ) 偏 导 数 ∂ z ∂ x , ∂ z ∂ y 必 定 存 在 函数z=f(x,y)在(x,y)可微分,那该函数在(x,y)偏导数 \dfrac{∂ z}{∂ x}, \dfrac{∂ z}{∂ y}必定存在 函数z=f(x,y)在(x,y)可微分,那该函数在(x,y)偏导数∂x∂z,∂y∂z必定存在,全微分 d z = ∂ z ∂ x Δ x + ∂ z ∂ y Δ y \mathrm{d}z=\dfrac{∂ z}{∂ x}Δ x+\dfrac{∂ z}{∂ y}Δ y dz=∂x∂zΔx+∂y∂zΔy ↩︎