数据结构—并查集《上》
今天主要介绍的是并查集这种数据结构。其本质上是解决某一些特定问题的而设计出的数据结构。大家可以了解下这种数据结构,作为自己知识的储备。
通过一个实际的问题引出并查集
假设有 n 个村庄,有些村庄之间有连接的路,有些村庄之间并没有连接的路
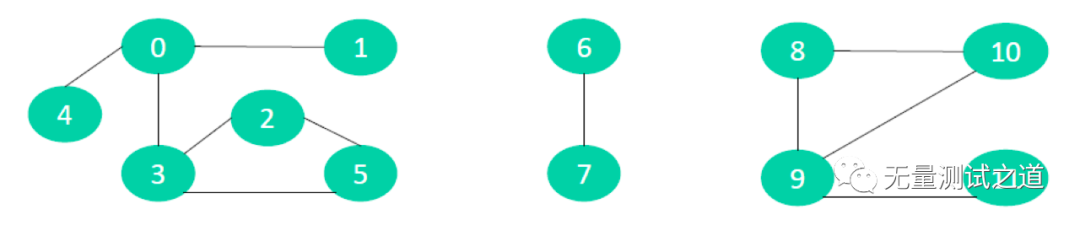
设计一个数据结构,能够快速执行 2 个操作:
-
查询 2 个村庄之间是否有连接的路
-
连接 2 个村庄
如果使用数组、链表、平衡二叉树、集合(Set) 都可以完成需求,但是查询、连接的时间复杂度都是 O(n)。
并查集能做到查询、连接的均摊时间复杂度都是 O(α(n)),α(n) < 5,非常适合解决这类“连接”相关的问题。
并查集(Union Find)
并查集也叫作不相交集合(Disjoint Set)
并查集有2个核心操作:
-
查找(Find):查找元素所在的集合
(这里的集合并不是特指Set这种数据结构,是指广义的数据集合) -
合并(Union):将两个元素所在的集合合并为一个集合
有 2 种常见的实现思路:
-
Quick Find
查找(Find)的时间复杂度:O(1)
合并(Union)的时间复杂度:O(n) -
Quick Union
查找(Find)的时间复杂度:O(logn), 可以优化至 O(𝛼(𝑛)), α(𝑛) < 5
合并(Union)的时间复杂度:O(logn), 可以优化至 O(𝛼(𝑛)), α(𝑛) < 5
如何存储数据?
假设并查集处理的数据都是整型,那么可以用整型数组来存储数据。
-
数组索引代表元素值
-
索引对应的值代表这个元素的根节点
将{0,1,2,3,4,5,6,7}存储到数组中,如下图:
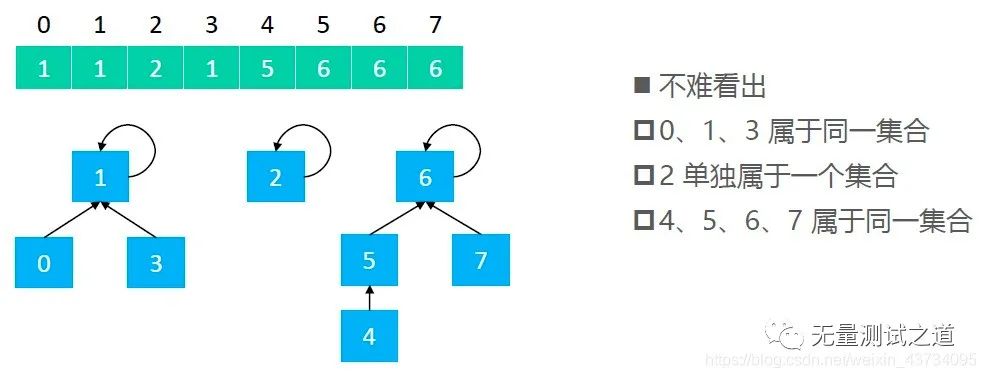
因此,并查集是可以用数组实现的树形结构(二叉堆、优先级队列也是可以用数组实现的树形结构)
并查集数据结构的接口定义
/** * 查找v所属的集合(根结点) */ public abstract int find(int v); /** * 合并v1、v2所在的集合 */ public abstract void union(int v1, int v2); /** * 检查v1、v2是否属于同一集合 */ public boolean isSame(int v1, int v2);
isSame()的实现十分简单
public boolean isSame(int v1, int v2){ return find(v1) == find(v2); }
元素的初始化
初始化时,每个元素各自属于一个单元素集合

private int[] parents; public UnionFind(int capacity){ if(capacity < 0){ throw new IllegalArgumentException("capacity must >= 1"); } parents = new int[capacity]; for (int i = 0; i < parents.length; i++) { parents[i] = i; } }
1.Quick Find
Quick Find 的 union(v1, v2)让 v1 所在集合的所有元素都指向 v2 的根节点。
并且 Quick Find 的高度永远保持 <= 2。
union 示例及实现
例如:
将{0,1,2,3,4,5}初始化为并查集,每个元素各自属于一个单元素集合:{0}, {1}, {2}, {3}, {4} 。

合并 1 和 0,union(1, 0),即 {1} 指向了 {2} 。

然后,合并 1 和 2,union(1, 2),1 所在集合有 {0, 1},即 {0, 1} 指向了 2 。

再合并 3 和 4,union(3, 4),即 {3} 指向了 {4} 。
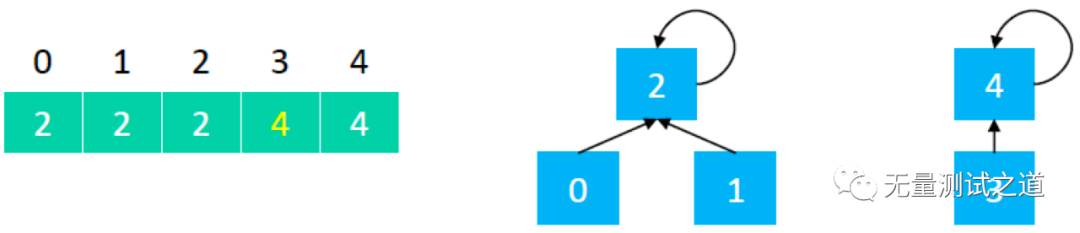
合并 0 和 3,union(0, 3),0 所在集合为 {0, 1, 2},3 所在集合为 {3,4},如下:
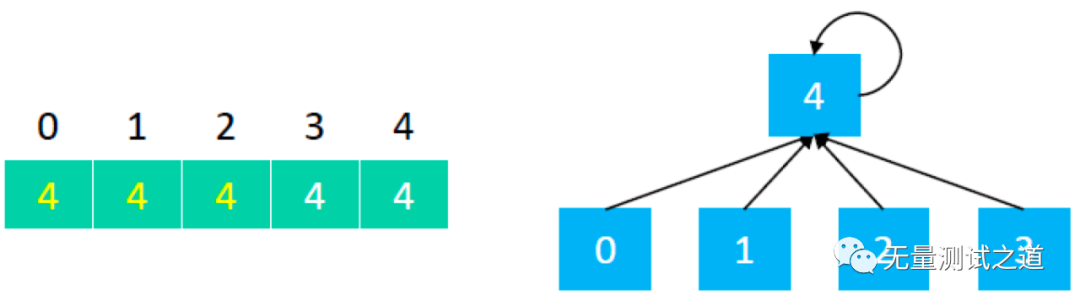
代码如下:
/** * 将v1所在集合的所有元素都嫁接到v2的父节点上 * v1 v2 union(v1,v2) * 0 4 4 * 1 2 3 0 1 2 3 */ public void union(int v1, int v2){ int p1 = parents[v1]; int p2 = parents[v2]; for (int i = 0; i < parents.length; i++) { if(parents[i] == p1){ parents[i] = p2; } } }
union 时间复杂度:O(n)
find 实现
Quick Find 查找的时候,由于数组中存储的就是根结点,因此直接取出即可。
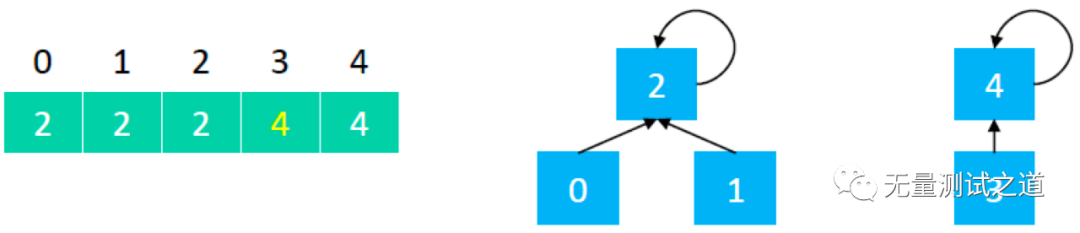
对上图执行 find(): find(0) == 2 find(1) == 2 find(2) == 2 find(3) == 4
/** * 父节点就是根节点 */ public int find(int v){ rangeCheck(v); return parents[v]; }
find 时间复杂度:O(1)
总结:
今天主要介绍了并查集这种数据结构,然后详细的讲述了Quick Find的实现思路。希望给大家的知识库增加一些新的知识储备。
欢迎关注【无量测试之道】公众号,回复【领取资源】
Python编程学习资源干货、
Python+Appium框架APP的UI自动化、
Python+Selenium框架Web的UI自动化、
Python+Unittest框架API自动化、
资源和代码 免费送啦~
文章下方有公众号二维码,可直接微信扫一扫关注即可。
备注:我的个人公众号已正式开通,致力于测试技术的分享,包含:大数据测试、功能测试,测试开发,API接口自动化、测试运维、UI自动化测试等,微信搜索公众号:“无量测试之道”,或扫描下方二维码:
添加关注,让我们一起共同成长!



