2024.8

1. [ARC181E] Min and Max at the edge

场上没人过的神题。（大概是搬运的官方题解）

先考虑如何 chk 一个图是否存在好生成树。观察好生成树的限制，发现其对于非树边的限制是在生成树上连接两点的路径有关。而 Kruskal 的证明就是对于每条非树边，其边权大于所有其路径上的树边，两者很像。

但是题目中的限制是点的限制，转到边上的想法是给点赋点权 \(X_i\)，然后 \((u,v)\) 的边权为 \(|X_u-X_v|\)。考虑把 \(X\) 设成一个递增的序列，比如 \(X_i=10^i\)，这样边权一定互不相同。

对于一棵好的生成树，设 \(S(u,v)\) 表示 \(u,v\) 之间的树上路径，则对于点 \(i\) 要求 \(\forall i\in S(u,v),X_u\leq X_i\leq X_v\)。而对于边 \((x,y)\)，\(X_u\leq X_x,X_y\leq X_v\)。设其根据上述定义的边权是 \(w(x,y)=|X_x-X_y|\)，则 \(\forall (x,y)\in S(u,v),w(x,y)<w(u,v)\)。这就证明了好的生成树一定是新图中的最小生成树。

因为可以构造出边权互不相同的情况，所以这也证明了好的生成树也是唯一的。跑出来这个图的最小生成树之后，检查每条非树边，如果都满足限制则该图是好的。

但是题目有多次询问，而且这个最小生成树也不是那么好求。不难发现其实图中定义的边权只需要满足 \(\forall i<j<k,w(i,j)<w(i,k)\) 并且 \(\forall i<j<k,w(i,k)>w(j,k)\) ，即满足区间包含单调性即可。

所以可以把边 \(w(u,v)\) 赋为 \(v\times(n+1)-u\)，这样得到的生成树一定满足对于任意非树边 \((u,v)\)，其路径上的最大值就是 \(v\)。原因是非树边 \((u,v)\) 路径上的边权应当都小于 \(w(u,v)\)，所以如果存在大于 \(v\) 的点则一定不合法。而且因为是 \(-u\)，所以合并两个连通块的时候，一边选择的较小的点会尽可能的大，这也满足路径上的最小值尽量是 \(u\)。

但是这样还是需要 chk 路径上点的最小值是否满足条件。可以再反着做一遍，\(w(u,v)=(n-u+1)\times(n+1)-(n-v+1)\)，同理得这样求出来的东西的最小值一定合法，最大值尽量合法。因为已经证明了好的生成树唯一，所以判一下两棵树是否相同即可。

这样就将问题转化成了比较好的形式：删边求最小生成树，可以看成是找一条非树边 \((x,y)\) 满足 \(x\in \text{subtree}(i),y\notin \text{subtree(i)},w(x,y)\) 最小。转成 dfn 序之后可以看成是两个 3-side 矩形查最小值，可以扫描线线段树维护，复杂度是 \(\mathcal O(n\log n)\)。

2. [ARC181F] Colorful Reversi

首先观察一下，对于 \(a,b,c,a\) 这种情况来说，两个 \(a\) 之间永远不可能发生操作。而 \(a,b,c,b,a\) 这种情况，两个 \(a\) 之间是有关联的。有一个很天才的想法是建树，一开始只有一个节点表示 \(a_1\)，维护一个指针 \(pos\) 表示当前在树上的哪个节点，接下来依次加入每个点 \(a_i\)：

1. 若 \(pos\) 所在点的颜色和 \(a_i\) 相同，则 \(pos\) 不动。
2. 否则若 \(pos\) 所在点有邻点的颜色是 \(a_i\)，则 \(pos\) 走向该邻点。
3. 否则新建一个节点，颜色为 \(a_i\)，\(pos\) 走向该节点。

这样就得到了一棵操作树，它有一些很好的性质：

1. 假设生成时在上面走过的路径是 \(B\)，则操作 \(l,r\) 等价于把 \(B[l,r]=\{x,y,y\dots y,y,x\}\) 变成 \(B[l,r]=\{x,x\dots x,x\}\)。
2. 对于原序列，如果能够操作 \([l,r]\) 则 \(l,r\) 一定属于同一个点，否则 \(l,r\) 属于不同的点。
3. 对于路径 \(\{v_1,v_2,v_3\dots v_k\}\)，通过操作将其变成 \(\{v'_1,v'_2,v'_3\dots v'_k\}\) 的最小代价是 \(\sum_{i=1}^k d(v_i,v'_i)\)，其中 \(d(x,y)\) 表示两点树上的距离。

接下来，对于 \(pos\) 的起始节点 \(x\) 和终止节点 \(y\)，最终序列的形态是若干个颜色段，而颜色恰好就是从 \(x\) 走到 \(y\) 所经过的简单路径上的颜色。证明很简单，显然路径上两个不同的颜色段永远无法合并，而如果存在其他的颜色则其两边的颜色一定是相同的，能再操作一次。

所以拉出树上 \(x,y\) 之间的路径，对于此路径外的部分一定会合并到路径上，可以先 dfs 一遍算出贡献，这样可以得到从 \(B\) 得到一个新的序列 \(C\)。接下来要解决问题的就是：现在有一个序列 \(C[1,n]\)，满足 \(\forall i<n,|C_i-C_{i+1}|\leq 1\)。现在要生成一个新的序列 \(C'\)，满足：

1. \(C'_1=C_1,C'_n=C_n\)。
2. \(\forall i<n,C'_{i+1}-C'_i\in[0,1]\)。
3. \(\forall i<n\wedge C'_{i+1}=C’_i+1,C_i=C'_i,C_{i+1}=C'_{i+1}\)。

在此基础上满足 \(\sum_{i=1}^n |C_i-C'_i|\) 最小。设 \(f_{i}\) 表示考虑了 \(\leq i\) 的 \(C\)，\(C'_i=C_i\) 时代价的最小值，\(pre_i\) 表示 \(C_i\) 上一次出现的位置。转移比较简单：

\[f_i=\min \begin{cases} f_{i-1}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad C_i=C_{i-1}+1\\ f_{pre_i}+\sum_{j=pre_i}^{i}|C_i-C_j|\;\;\;\;\;pre_i\not=-1 \end{cases} \]

因为 \(pre_i\) 是上一次出现的位置，所以对于所有的 \(j\) 要么 \(C_j\) 全部大于 \(C_i\)，要么全部小于 \(C_i\)，可以前缀和处理一下 \(\mathcal O(1)\) 转移。这样 \(f_n\) 加上之前把树缩成一条链的代价就是答案，复杂度是 \(\mathcal O(n)\) 或 \(\mathcal O(n\log n)\)。

3. CF1988F Heartbeat

最大值把序列分成两部分，前一部分对前缀最大值个数有贡献，后一部分对后缀最大值个数有贡献，可以分开算。

设 \(f_{i,j,k}\) 表示 \([1,i]\) 的排列，有 \(j\) 个前缀最大值，\(k\) 个上升的位置的方案数。不断向右边加数不好做，不断加入 \(n+1\) 也不好做，因为可能前缀最大值个数会变少。所以考虑不断的加入新的 \(1\)，把原来的值域整体平移。转移比较平凡：

1. \(1\) 放在最前面：\(f_{i+1,j+1,k+1}\leftarrow f_{i,j,k}\)。
2. \(1\) 放在最后面：\(f_{i+1,j,k}\leftarrow f_{i,j,k}\)。
3. \(1\) 放在上升的位置中间：\(f_{i+1,j,k}\leftarrow f_{i,j,k}\times j\)。
4. \(1\) 放在下降的位置中间：\(f_{i+1,j+1,k}\leftarrow f_{i,j,k}\times (i-1-j)\)。

预处理这部分的复杂度是 \(\mathcal O(n^3)\) 的。然后把两个拼起来的时候，前后缀最大值个数的贡献可以提前算，上升位置个数的贡献最后算。然后发现转移是二维卷积，可以拉插。

4. P10008 [集训队互测 2022] Range Minimum Element

难点在于双射构造。

首先考虑给定了 \(b\) 如何进行判定。从小到大填数 \(x\)，每次把能填的地方（\(b_i>x\) 的区间之外）全部填上 \(x\)，这样填一定是最优的。合法当且仅当这样生成的序列 \(a\) 对应的 \(b\) 就是 \(b\) 本身。

发现通过这样的生成方式，合法的 \(a\) 和 \(b\) 是一一对应的，所以对 \(b\) 计数可以转为对能被这样生成的 \(a\) 计数。

如果给定了 \(a\)，如何判 \(a\) 是否合法？找到第一个最小值的位置 \(p\)，把 \(A[1,n]\) 变成 \(A[1,p-1]\) 和 \(A[p+1,n]\)。因为 \([1,p-1]\) 中并没有被填上最小值，所以被 \([1,p-1]\) 包含的区间一定选择的都是大于最小值的数，并且他们的的并集一定是 \([1,p-1]\)。然后递归判断 \(A[1,p-1]\) 和 \(A[p+1,n]\) 是否合法。

上述过程是值域从小到大，分裂序列。计数就考虑值域从大到小，合并序列。\(f_{l,r,x}\) 表示区间 \([l,r]\) 填入了 \([x,c]\) 中的数的方案数。转移就是枚举最小值的位置 \(p\)：

\[\begin{aligned} f_{l,r,x}&\leftarrow [[l,r]\text{合法}]\times f_{l,r,x+1}\\ f_{l,r,x}&\leftarrow [[l,p-1]\text{合法}]\times f_{l,p-1,x+1}\times f_{p+1,r,x} \end{aligned} \]

第一种转移表示区间内没有 \(=x\) 的数。预处理合法区间，暴力做复杂度是 \(\mathcal O(n^3c)\)。套路性的，不难归纳证明 \(f_{l,r,x}\) 是一个关于 \(x\) 的 \(\mathcal O(r-l)\) 次多项式，可以拉插。

5. [ARC179E] Rectangle Concatenation

并不困难。只是唐完了。

稍微观察一下发现矩形只有两种形态。考虑暴力：从每个 \(i\) 开始向后扫，设 \(f_{j,0}\) 表示能否拼在左右，\(f_{j,1}\) 表示能否拼在上下。设 \(S_{l,r}\) 表示 \([l,r]\) 内矩形的面积和，没想到用面积判就败了：

\[\begin{aligned} f_{j,0}=(f_{j-1,0}\wedge x_j=x_{j-1})\vee(f_{j-1,1}\wedge S(i,j-1)=y_{j-1}x_j)\\ f_{j,1}=(f_{j-1,1}\wedge y_j=y_{j-1})\vee(f_{j-1,0}\wedge S(i,j-1)=x_{j-1}y_j)\\ \end{aligned} \]

考虑优化：把 \(j\) 从左向右扫，维护合法的 \(i\)。设 \(S_0\) 表示 \(f_{j,0}\) 合法的 \(i\) 集合，\(S_1\) 同理。发现 \(j+1\) 的时候，观察式子左半部分，\(S_0,S_1\) 可能会做一个清空操作。

咋回事啊，感觉用面积判定大概是想到了的。一直在瞎想维护两个矩形如何在最左边加。哎。
右半部分看成面积前缀和相减，合法的 \(i\) 是唯一的。是一个单点加入，容易维护。还需要拿一个桶维护 \(|S_0\cup S_1|\)。时间复杂度 \(\mathcal O(n\log n)\) 或者 \(\mathcal O(n)\)。

6. [ARC182F] Graph of Mod of Linear

首先判掉 \(A\leq 1\) 的情况。把问题分为 \(A,N\) 是否互质。

1. \(A\not \perp N\)

首先定义 \(f^K(i)\) 表示从 \(i\) 开始走 \(K\) 步会走到哪。显然：

\[f^K(i)=A^Ki+B\sum_{j<K}A^j=A^Ki+B\frac{A^K-1}{A-1} \]

然后是一步神奇的转化。我们希望能只保留在环上的点，而 \(f^N(i)\) 一定在环上，并且对于 \(i\in[0,N-1]\)，\(f^N(i)\) 一定涵盖了所有在环上的点（所有在环上的点的 \(f\) 已经涵盖了）。所以环上的点可以表示为：

\[iA^N+B\frac{A^N-1}{A-1}\bmod N \]

对于 \(i\) 向后走一步：

\[A(iA^N+B\frac{A^N-1}{A-1})+B\equiv jA^N+B\frac{A^N-1}{A-1}(\bmod\;N) \]

取 \(d=\gcd(A^N,N)\)：

\[j=Ai+\frac{A^N}{d}B(\bmod \frac{N}{d}) \]

所以问题可以从 \((A,B,N)\) 变为 \((A\bmod \frac N d,B\frac{A^N} d\bmod \frac N d,\frac N d)\)，转成了互质的情况。

2. \(A\perp N\)

设 \(C_i\) 表示第 \(i\) 个点所在的环长，则 \(\sum \frac 1 {C_i}\) 就是答案。

从 \(i\) 开始走 \(K\) 次走回自己，要求的就是：

\[\begin{aligned} A^Ki+B\frac{A^K-1}{A-1}\equiv i(\bmod \;N)\\ A^K\equiv 1(\bmod \;\frac{N(A-1)}{\gcd(N(A-1),i(A-1)+B)}) \end{aligned} \]

把模数再变形一下。设 \(d=\gcd(A-1,B)\)，令 \(A'=\frac{A-1}{d}\)，\(B'=\frac B d\)，则：

\[A^K\equiv 1(\bmod \;\frac{NA'}{\gcd(NA',iA'+B')}) \]

此时 \(A',B'\) 已经互质，所以 \(NA'\) 的贡献只有 \(N\) 中的因子。设 \(N'=\frac{N}{\gcd(N,A'^N)}\)，则：

\[A^K\equiv 1(\bmod \;\frac{NA'}{\gcd(N',iA'+B')}) \]

令 \(y=(iA'+B )\bmod N'\)，则如果 \(i\in [0,N-1]\)，则每个 \(y\) 都一定恰好被覆盖了 \(\frac N {N'}\) 次。所以现在要求的就是：

\[\frac N{N'}\sum_{i|N'} C_i\varphi(\frac{N'}{i}) \]

其中 \(C_i\) 是满足 \(A^{C_i}\equiv 1(\bmod \frac{NA'}{\gcd(N',i)})\) 的最小整数。

首先有性质：

1. 若 \(x|y\)，则 \(\varphi(x)|\varphi(y)\)。
2. \(A^k\equiv 1(\bmod \;n)\) 的解都是 \(\varphi(n)\) 的因数并且 \(k\) 一定能被表示成 \(xk_0\)，其中 \(k_0\) 表示最小解。

若 \(n1\leq n2,n1|n2,n2|N'\)，则：

\[\begin{aligned} A^{C_1}&\equiv 1(\bmod \frac{NA'}{n1})\\ A^{C_1}&\equiv 1(\bmod \frac{NA'}{n2})\\ A^{C_2}&\equiv 1(\bmod \frac{NA'}{n2})\\ \end{aligned} \]

所以 \(C_1\) 一定是 \(C_2\) 的倍数。所以可以用记忆化搜索的方式求解所有的 \(C\)：考虑把 \(\varphi(NA')\) 质因数分解，\(C_1\) 初始化为 \(\varphi(NA')\)，然后不断尝试除 \(\varphi(NA')\) 的因子，继续用快速幂判是否合法。

这样求出 \(n=1,C_1\) 的答案，然后将 \(n\) 乘一个 \(\frac{N'}{n}\) 的质因数，令 \(C'\) 初始化为 \(C_1\)，再进行不断尝试除质因子的过程。复杂度一个很松的上界是 \(\mathcal O(q\omega_{max}(10^{12})d_{max}(10^{12})))\)，\(w\) 表示质因子个数，\(d\) 表示因数个数。但是完全跑不满，所以还是能过的。

7. [ARC178E] Serval Survival

非常生气，点开一道看起来很正常的计数，推着推着就发现需要多项式/fn。

首先对于“撞上了之后调头”这种东西有经典的思想：可以看成是互相穿过并没有调头。但是因为要求第 \(i\) 只猫走过的路，所以可以看成是和撞上的猫互换身份。

手玩一下可以发现，如果第 \(i\) 只猫向左走，它会和 \(a_i\) 左边的第一只向右的猫互换身份，然后和 \(a_i\) 右边的第一只向左的猫互换身份，然后和 \(a_i\) 左边的第二只猫向右的猫互换身份\(\dots\)，位置指的都是初始位置。

第 \(i\) 只猫走的路程就等于最后一只和他交换身份的猫直走能走的路程（向右为 \(L-a_i\)，向左为 \(a_i\)）。据此，我们可以找出第 \(i\) 只猫的策略。

设 \(a_i\) 左边向右走的猫的集合为 \(L\)，\(a_i\) 右边向左走的猫的集合为 \(R\)，分类讨论：

1.\(|L|>|R|\)

如果他向左走，最后和他交换身份的猫是 \(L\) 中从右向左第 \(|R|+1\) 只猫。如果他向右走则是 \(L\) 中从右向左第 \(|R|\) 只猫。因为是向右走，显然靠左边的猫一定走的更远，所以此时他一定会向左走。

2.\(|L|<|R|\)

和上文同理，一定会选择向右走。

3.\(|L|=|R|\)

此时他有两种策略：选择 \(L\) 中最靠左的 \(L-a_i\) 和 \(R\) 中最靠右的 \(a_i\)，这是唯一有决策的点，需要选较大值。

考虑暴力 DP：设 \(ans_i\) 表示第 \(i\) 只猫的答案。

第一种情况 \(|L|>|R|\)：

\[\begin{aligned} ans_i&=\sum_{j=1}^i(L-a_j)2^{j-1}\sum_{k=0}^{i-j-1}\binom{i-j-1}{k}\binom{n-i}{k}\\ &=\sum_{j=1}^i(L-a_j)2^{j-1}\binom{n-j-1}{n-i}\end{aligned} \]

上面使用了范德蒙德卷积化简。发现组合数可以拆成 \(i,j,i-j\) 相关的式子，可以 FFT。

对于 \(|L|<|R|\) 的情况同理，可以把整个序列倒过来做一遍。

第二种情况 \(|L|=|R|\)，假设最大值在右侧取到：

\[\begin{aligned} ans_i&=\sum_{j=i+1}^n a_j\sum_{k=0}^{j-i-1}\binom{j-i-1}{k}\binom{i-L_j}{k+1}\\ &=\sum_{j=i+1}^n a_j\binom{j-1-L_j}{i-1-L_j} \end{aligned} \]

\(L_i\) 表示最小的 \(j\) 满足 \(m-a_j<a_i\)。还是范德蒙德卷积，但是这个式子并不好用 FFT 处理。考虑写成生成函数形式，令 \(Ans(x)\) 表示 \(\sum_{i=0}^n ans_i x^i\)，则：

\[Ans(x)=\sum_{j=2}^n a_j (1+x)^{j-1-L_j}x^{1+L_j} \]

\((1+x)^{j-1-L_j}\) 是为了构造组合数系数，\(x^{1+L_j}\) 是因为 \(j\) 对 \(i\) 贡献，\(i\) 的下指标是 \(i-L_j-1\)，需要做一个整体平移。

因为 \(L\) 是单减的，\(i-1-L_i\) 是单增的，可以分治解决：设 \(A_i\) 表示 \(L_i+1\)，\(B_i\) 表示 \(i-1-L_i\)，\((1+x)^{B_l}x^{A_r}F_{l,r}(x)\) 表示 \(l,r\) 区间对答案的贡献。合并：

\[F_{l,r}(x)=F_{l,mid}(x)x^{A_r-A_{mid}}+F_{mid+1,r}(x)(1+x)^{B_{mid+1}-B_l} \]

合并的时候暴力 FFT 即可。这样最终答案就是 \((1+x)^{B_{pos}}x^{A_n}F_{pos,n}(x)\)，\(pos\) 表示最小的 \(i\) 满足 \(i-1-L_i>0\)。因为 \(A,B\) 的值域都是 \(n\) 的，一个点最多被 \(\log n\) 次 FFT 包含，可以分析出复杂度是 \(\mathcal O(n\log^2 n)\)。

8. *P10896 移言丁真：Unavoided linyue

首先考虑确定了所有串怎么求最小值。首先每个串肯定是内部尽量匹配，然后左边剩了若干个右括号，右边剩了若干个左括号。设 \(L_i\) 表示左边右括号的数量，\(R_i\) 表示右边左括号的数量。

手玩一下，观察任意一个拼接方式，尽量匹配之后，一定是有一个串作为中点，他左边最终只剩下了右括号，右边只剩下了左括号。所以考虑钦定一个串作为中点。剩下的串若 \(L_i<R_i\) 则拼接在右边，否则拼接在左边。

显然钦定作为中点的串的 \(\min(L_i,R_i)\) 应当尽量的大，所以答案即为 \(\sum_{x\in S}\min(L_x,R_x)-\max_{x\in S}(\min(L_x,R_x))\)。

先统计 \(\sum_{x\in S}\min(L_x,R_x)\)。看成网格图，左括号是 \(+1\)，右括号是 \(-1\)，则要求从 \((i,0)\) 出发，中途纵坐标的最小值为 \(0\)，最后的纵坐标大于等于 \(i\)。荣斥一下变成最小值 \(\geq 0\) 减去最小值 \(\geq 1\)，旋转 \(45^{\circ}\) 之后做一个反射荣斥即可。答案是：

\[\begin{aligned} f(n)=&\sum_{i=0}^ni\sum_{j\geq \lceil\frac n 2\rceil}(\binom{n}{j}-\binom{n}{j+i+1})-(\binom n j-\binom n {j+i})\\ =&\sum_{i=0}^ni\binom{n}{i+\lceil\frac n 2\rceil} \end{aligned} \]

对于最小值再右边的情况要求左边最后大于起点，只有上取整变成 \(+1\) 之后除二上取整。这个式子可以暴力算。

对于 \(\max_{x\in S}(\min(L_x,R_x))\)，可以枚举 \(i\)，计算 \(\max\geq i\) 的情况数，即存在一个 \(\min(L_x,R_x)\geq i\)。可以用 \(2^n\) 减去全都 \(\min(L_x,R_x)<i\) 的。所以答案就是：

\[\sum_i 2^n-\prod(2^{len}-\binom{len}{i+\lceil\frac {len} 2\rceil}-\binom{len}{i+\lceil\frac {len+1} 2\rceil}) \]

可以暴力计算。最后还有内部匹配的贡献，看成 \(\frac{len-l-r}{2}\)，和计算 \(f\) 一样的方式计算即可。

9. [ARC083F] Collecting Balls

建图，连边 \((x_i,y_i+n)\)，这样会形成一个基环树森林。对于基环树的每条边，需要把他归到他连接的两个点中任意一个，并且每个点只能拥有一条边。

对于每个基环树分别计算，树边归属的点一定是它两端深度较大的那个，环边归属点整体只有两种方式：顺时针和逆时针。确定了边挂在那个环上时候，操作顺序的限制就是，如果边 \((x,y)\) 归到了点 \(y\)，则要求所有 \((y,z),z<x\) 的边需要在它之前操作。

把边看成点，再建一个图，不难证明这是一个森林：对于树边之间显然只有从下到上的边，环边上的边形成了若干条链，还有一些环边指向树边的边，所以一定是外向树森林。拓扑序计数对于一棵树就是 \(\frac{n!}{\prod siz_i}\)，\(siz\) 表示子树大小。

10. [ARC177F] Two Airlines

有点魔怔的题。

一个基本的观察是如果当前某个人 \(A\) 拿着盒子走到了位置 \(i\)，那位置小于 \(i\) 的人一定永远没用了。如果之后要用到前面的人 \(B\)，就应当让 \(B\) 拿着盒子走到 \(i\) 而不是让 \(A\)，这样 \(A\) 待在原来的位置，代价一定不会更劣。

再手玩一下，可以发现每次的过程都是：某个人 \(A\) 拿起盒子，走到某个地方。然后后面来了一个和 \(A\) 颜色不一样的人（或者是本身就在这个地方的人），走到了 \(A\) 现在的位置，然后带着箱子走了，此时 \(A\) 也已经没有用了。

进一步的，“后面来人”的这个过程，对于每种颜色内部，一定是先用坐标尽量小的人来。这个结论不难用调整法证明。

而最优解一定能用上述过程刻画出来。所以可以设 \(f_{i,j,k,0/1}\) 表示当前盒子在 \(i\)，被 \(0/1\) 颜色的人拿着，\(i\) 后面的 \(j\) 个颜色为 \(0\) 的人已经用过了（此时在 \(<i\) 的位置），\(k\) 个颜色为 \(1\) 的人已经用过了。转移 \(\mathcal O(1)\)，状态数和复杂度都是 \(\mathcal O(n^3)\) 的。

接下来的一个想法观察性质，能不能简化一维状态什么的，但是好像不太好做。除此之外比较自然地，可以感受到 \(j,k\) 都不会太大，设成 \(20\) 左右，交上去就直接过了。下面证明 \(j,k\) 都只需要取到 \(\log n\)。

直观感受一下，“后面来人”的原因一定是，\(i\) 后面有一段比较长的和当前拿着箱子的颜色不同的路。

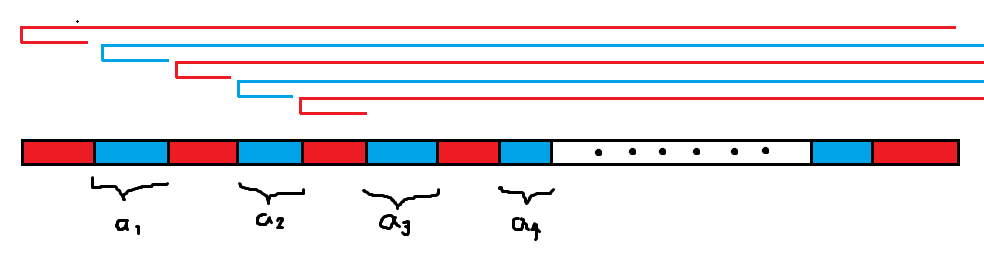
红色和蓝色的块分别表示序列上红色和蓝色的连续位置。红色段里面不一定全部都是红色，蓝色段里也不一定全是蓝色。红色和蓝色的线条表示人走过的路程。\(a_i\) 表示这个蓝色段里面有多少个蓝色格子。

称除去搬运盒子过程中造成的代价为“额外代价”。因为第二条红色线条走到他的目标位置（第二个红块）额外花费了 \(\sum_{j\geq 2}a_j\) 的代价，所以 \(a_1>\sum_{j\geq 2}a_j\)，否则可以让第一个人直接走到第二个红色段：

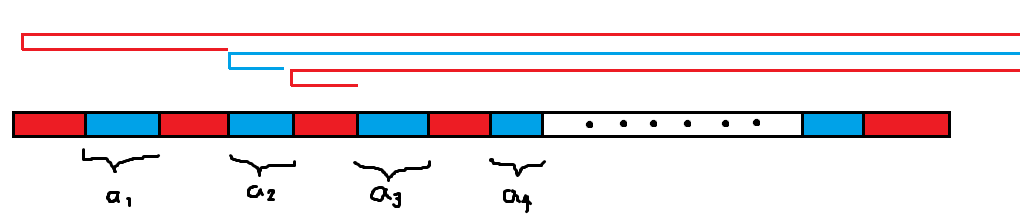
这样一定不劣。后面的同理，\(a_i>\sum_{j>i}a_j\)，所以最多 \(\log\) 轮之后 \(a_i\) 就要超出值域了。所以 \(j,k\) 的维度都只需要开到 \(20\)。预处理一下还是能做到 \(\mathcal O(1)\) 转移。总复杂度 \(\mathcal O(n\log^2 n)\)。

11. [ARC176D] Swap Permutation

对每个位置分别算贡献。一个很重要的观察是其他所有数都是等价的（非常神奇）。设 \(A\) 表示原来 \(i\) 位置上的数，\(B\) 表示原来 \(i+1\) 位置上的数，\(C\) 表示其他的数，设 \(f_{0\sim 7}\) 表示经过 \(m\) 次操作之后 \(AB,BA,AC,CA,BC,CB,CC\) 的概率。每个位置 \(i\) 的 \(f\) 都是相同的。转移系数应该比较容易手搓出来，预处理 \(f\) 可以暴力 DP，也可以矩阵快速幂（所以其实可以做 \(m=10^{18}\) 的）。然后对于每个位置分类算贡献即可。总复杂度 \(\mathcal O(n+T^3\log m)\)，其中 \(T=7\)。

12. [ARC183D] Keep Perfectly Matched

这场不打感觉亏麻了，怎么大家都不会 D。首先匹配路径长度之和最大，很典的想到取重心，猜测答案上界 \(\sum_i dep_i\) 可以取到。

取完重心之后，希望不断把两个不同的子树里的点进行匹配，直到删空。因为原树本身存在完美匹配，所以找一对不同子树里的点删去后，根节点的匹配一定变了。

所以选的点一定有一个在根节点当前的匹配点的子树里，否则根节点没有理由更改匹配点。设这个点为 \(x\)，则 \(x\) 一定满足：其到根的路径上，边的种类是“匹配边，非匹配边，匹配边...”，即：

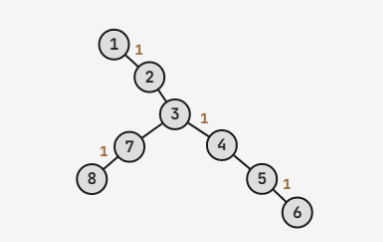
图中标 \(1\) 的边是匹配边，可以发现删六号点是合法的，而删 \(8\) 号点的过程中会因为连续出现了两条非匹配边而寄掉。

这样确定了一个子树中的点，另一个点是可以任意选的。因为要尽量匹配对，所以另一个点应该选在除此之外的 \(siz\) 最大的子树里面。接下来根的匹配就是选的第二个子树中的根节点。继续做上述过程即可。

这样做为何能取到最优值：设 \(x\) 是根的初始匹配节点，首先第一次删点的两棵子树一定分别是 \((x,y)\)，然后第二次因为此时根和 \(y\) 匹配，所以要删 \((y,z)\)，以此类推，可以发现除了开始的 \(x\) 删了一个点，剩下的操作都是，选一个子树删两个点，然后跳到另一棵子树。

除了 \(x\) 子树大小是奇数，剩下的子树大小都是偶数，一开始 \(x\) 删了 \(1\) 就全部变成了偶数。所以不会有奇偶性不对的情况。如果跳到另一棵子树选择当前 \(siz\) 最大的，那就一定能够删空。因为此时根是树的重心，每个子树内需要的操作次数大小都不会超过 \(\frac m 2\)，其中 \(m\) 是总操作次数，所以这样做一定不会爆掉。

现在的问题就是如何高效的找出当前能删掉的合法点。策略也很简单：对于点 \(x\) 来说，如果初始他的匹配是他的父亲，则他儿子可以按任意顺序一个一个删光。

如果初始他的匹配是他的某个儿子，则先把这个儿子全部删空时最优的。然后他的匹配就变成了他的父亲，他剩下的儿子可以任意排列。

可以 \(\text{dfs}\) 求出每个子树的后序遍历，如果有某个儿子和他匹配就优先向这个儿子走，这样可以求出每个点的合法操作序列。然后套用上述过程，总复杂度 \(\mathcal O(n\log n)\) 或者 \(\mathcal O(n)\)。

13. 炫酷原神

题如其名。每种颜色分别算贡献，子区间个数看成所有连续区间选 \(2\) 个可重位置。

设 \(f_{i,0/1/2/3/4}\) 表示，当前在位置 \(i\)，\(0\) 表示剪贴板是对的并且当前区间没选数的概率，\(1\) 表示剪贴板是对的并且当前区间选了一个数，\(2\) 表示答案，\(3\) 表示剪贴板是错的并且当前区间没有选数，\(4\) 表示剪贴板是错的并且当前区间在剪贴板是对的的时候选了一个数。每种颜色都这么做一遍，对的颜色的 Ctrl C 的系数矩阵（行向量在左，矩阵在右）是：

\[\begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ \frac 1 2 & 0 & 0 & \frac 1 2 & 0\\ 0 & \frac 1 2 & 0 & 0 & \frac 1 2\\ \end{bmatrix} \]

然后是 Ctrl V：

\[\begin{bmatrix} 1 & \frac 1 2 & \frac 1 2 & 0 & 0\\ 0 & 1 & \frac 1 2 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & \frac 1 2 & 0\\ 0 & 0 & 0 & 0 & \frac 1 2\\ \end{bmatrix} \]

遇到错的颜色的 Ctrl C：

\[\begin{bmatrix} \frac 1 2 & 0 & 0 & \frac 1 2 & 0\\ 0 & \frac 1 2 & 0 & 0 & \frac 1 2\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{bmatrix} \]

线段树维护区间矩阵乘积。虽然有 \(26\) 棵线段树但是每次实际只会改两棵。\(\mathcal O((n+q)\log n5^3)\)，需要一定常数优化：可以把矩阵展开，发现比如 \(2\) 对 \(0\) 和 \(1\) 永远没有贡献，\(4\) 和 \(1\) 对 \(0\) 也永远没有贡献，去掉一些冗余的乘法，实际上 \(5^3\) 远远跑不满。

14. *王者题目

没听题解，自己糊的，不知道对不对。

首先经过一些简单的观察，有大于四度的点答案一定为 \(0\)，并且四度点最多只有一个。有四度点的话，确定了四度点填啥别的都基本确定了，比较平凡。

然后考虑树，\(1\) 如果填在二度点或者三度点上比较平凡，只考虑 \(1\) 在叶子上。首先暴力是枚举每个叶子作为根填 \(1\)，\(f_i\) 表示如果 \(i\) 填 \(1\)，其子树内填成一个连续的值域前缀的方案数。

第一种转移：

即在一条链上向下走三步，容易发现 \(4\) 之后的是一个子问题。

第二种转移：

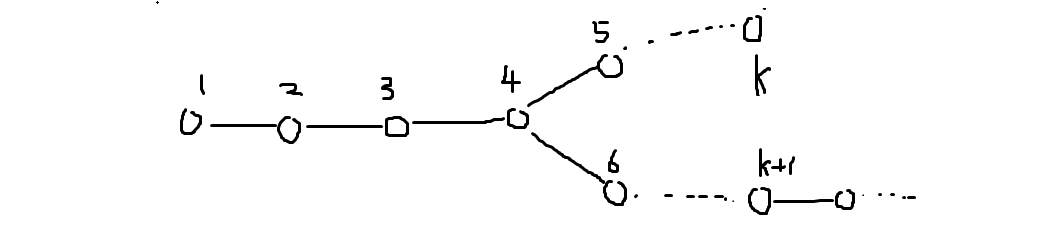
即填数到第一个分叉路口的时候，前面的值域都填满了。设三度点填的是 \(x\)，则后面只能填 \(x+1\) 和 \(x+2\)，然后只能填 \(x+3,x+4\dots\)，直到一条链似掉，此时 \(k+1\) 之后递归进子问题。

第三种转移：

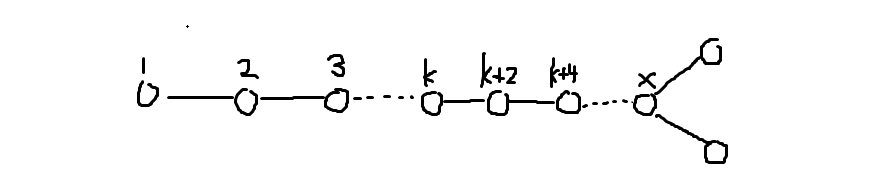
此时 \(k+1,k+3\dots x-1\) 都没有填，\(x\) 旁边的两个点可以填 \(x-1,x+1\) 和 \(x+2\)。分类讨论：

填 \(x-1\) 和 \(x+1\)

这种情况比较简单，画一下发现填 \(x-1\) 的那端必定是一条长度为 \(\frac{x-k}2\) 的链，\(x+1\) 那端直接递归进了子问题。

填 \(x-1\) 和 \(x+2\)

\(x-1\) 补完了 \(\frac {x-k}{2}\) 之后旁边如果还有空的点，只能填 \(x+1\)，是类似第二种转移的两条链，直到一条链似掉之后进入子问题。

而如果 \(x-1\) 旁边没有空的点，此时递归到了一个“子树根填 \(2\)”的子问题，可以设 \(g_i\) 表示 \(i\) 填了 \(2\) 然后子树内填成一个满的值域前缀方案数，转移和 \(f\) 一样，唯一的一种额外方式是，如果 \(i\) 旁边有连着一度点的三度点，则可以三度点填 \(3\)，然后一度点填 \(1\)，然后三度点连着的另一个点的 \(f,g\) 都可以贡献过来。

填 \(x+1\) 和 \(x+2\)

\(x+1\) 一定要补全 \(x-1,x-3\dots k+1\)，然后如果 \(x+1\) 旁边还有空点，一定填 \(x+3\)，然后进入两条链的情况。如果 \(x+1\) 旁边没有空点则 \(x+2\) 直接递归进子问题。

第四种转移

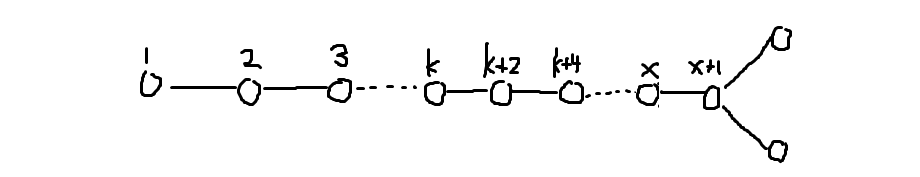
此时 \(x+1\) 旁边的点一定填了一个 \(x-1\) 并只有一条链，另一个可以填 \(x+2\) 也可以填 \(x+3\)，可以从 \(f\) 和 \(g\) 转移过来。

第五种转移（结尾）

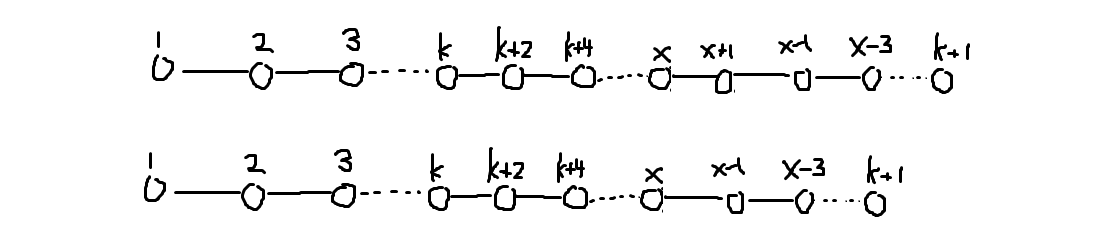
两种都比较平凡。总复杂度 \(\mathcal O(n^2)\)，不知道能不能换根做 \(\mathcal O(n)\)。不想写。

15. [ARC183E] Ascendant Descendant

一个直接的想法是求出 \(L_i,R_i\) 表示极大的区间 \([L_i,R_i]\) 满足 \(\forall j\in[L_i,R_i],b_j\in \text{subtree}(a_i)\)。由于树的性质，\([L_i,R_i]\) 之间要么相离，要么包含。

但是 \(L_i,R_i\) 并不是 \(i\) 能真正到达的点。因为 \(i\) 只能一个一个交换过去，中途可能会有一些点阻碍着 \(i\) 的交换。具体的，把 \([L_i,R_i]\) 构成的树形结构建出来，会阻碍交换的点就是满足 \(siz_i=R_i-L_i+1\) 的整棵子树。必要性和充分性都比较显然。（但是想不到啊）

求 \([L_i,R_i]\) 是平凡的，一个 \(\mathcal O(1)\) LCA 和线段树或者 ST 表就能在 \(\mathcal O(m\log m)\) 的时间里求出来。后半部分实现的时候可以按照区间长度排序，拿一个 BIT 维护区间和，每次是区间内任选一个点单点加一即可。再用一个 'set' 维护删掉的点。总复杂度 \(\mathcal O(n\log n)\)。

16. [ARC180E] LIS and Inversion

首先考虑要求代价为 \(0\) 的一个暴力 DP：\(f_{i,j}\) 表示填了前 \(i\) 个数，此时相对值域末尾为 \(j\) 的数结尾的 LIS 的最大值。填第 \(i+1\) 个数的时候，把它插在某两个数之间，所以转移是：

\[f_{i,j}= \begin{cases} f_{i-1,j-1}\qquad\qquad\qquad j>i-a_{i}\\ \max_{k<j}\{f_{i-1,k}+1\}\quad 1<j\leq i-a_{i}\\ 1\qquad\qquad\qquad\qquad\;\; j=1\\ \end{cases} \]

经过观察，可以发现取前缀最大值的操作是不必要的，第二种情况可以直接令 \(f_{i,j}=f_{i-1,j-1}+1\)。

证明：假设存在 \(f_{i-1,k}>f_{i-1,j-1}\)，应当用 \(k\) 贡献到 \(j\)。但是因为 \(k+1\leq j\leq i-a_i\)，所以 \(k+1\leq i-a_i\)，所以此时 \(f_{i,k+1}\geq f_{i-1,k}+1\)。在 \(f\) 相同的情况下，显然是下标越小的越有前途，所以 \(k+1\) 不劣于 \(j\)，\(j\) 是没有用的。

这样 \(f\) 的转移就变成了：先平移一位，在最前面加入 \(0\)，然后做一个 \([1,i-a_i]\) 的前缀 \(+1\) 的操作。然后可以进一步发现，如果允许代价为 \(k\)，则可以看成把 \(k\) 个位置的 \(a_i\) 变成 \(0\)，即前缀加变成了全局加。

所以考虑统计每个位置被多少次前缀加覆盖，这可以用差分简单实现，这样就求出来了 \(f\)。在最后位置 \(i\) 的答案上界是 \(i\)，所以可以花费 \(j\) 的代价（\(j\leq i-f_i\)）来获得一个 \(f_i+j\) 的答案。

17. [ARC175E] Three View Drawing

哎，构造。

首先考虑 \(m=n^2\) 怎么做：显然是最上面一层填满第一条主对角线，第二层填满第二条主对角线...（主对角线指可以循环的对角线）。

把 \(n\) 变成满足 \(n^2\geq m\) 的最小的 \(n\)。然后考虑删去 \(n^2-m\) 个。可以发现（谁能发现啊啊啊）在矩形的右下角删掉一个 L 型即可。如果 \(n^2-m\) 是偶数则右下角的 \((n,n,n)\) 保留即可。

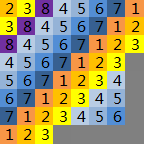
设 \(x\) 表示 \(L\) 的边长 \(-1\)（图中为 \(4\)）。上图是正方体的俯视图，把正方体从上到下分成 \(1,2,3\dots n\) 层，某个位置填了 \(x\) 代表这个的格子存在于第 \(x\) 层。

首先对于暖色调的填法，可以发现这样对于前 \(n-1-x\) 层，从正面和侧面看都是填满的，和俯视图是相同的。

对于紫色，这个位置填的是 \(n\)，正好对应了在第 \(n\) 层只有最左边三个有值，符合俯视图。

对于冷色调的其他颜色，都在一个 \((n-1)\times(n-1)\) 的正方形里面填的，所以对于第 \((n-x)\sim(n-1)\) 层，每层从正面和右面看都是恰好 \(n-1\) 个格子，也符合俯视图。