初等双射构造

My Blogs

下文中 \([n]\) 表示 \(\{1,2,3\dots n\}\)。

P0

对于正整数 \(n\)，称 \(a_{1\dots k}\) 是 \(n\) 的有序划分，当且仅当 \(\sum_i a_i=n\)。给定 \(n(\geq 2)\)，求满足 \(\sum_{i}[2|a_i]\) 是偶数的有序划分个数。

答案：\(2^{n-2}\)。

\(n\) 的所有划分可以看成有 \(n-1\) 个空位，每个空位可以放板或不放，总方案数是 \(2^{n-1}\)。现在只需要证明偶数的个数一半是奇，一半是偶。

对于一个有序划分，若 \(a_1=1\)，则把 \(a_1\) 和 \(a_2\) 合并在一起。否则把 \(a_1\) 拆成 \(1\) 和 \(a_1\)。经过这样的操作，一定会改变偶数个数的奇偶性。

上述映射是一个 对合，即 \(f=f^{-1}\)。这样就证明了奇偶两边的数量相等。

注意构造对合的时候不能映射到自己。

P1

\[\sum_{k=0}^m\binom{m+k}{k}2^{-k} \]

答案是 \(2^m\)。考虑一个长度为 \(2m\) 的 \(01\) 序列，显然有 \(2^{2m}\) 种。变形一下上式：

\[\sum_{k=0}^m\binom{m+k}{k}2^{m-k} \]

对于一个序列，若 \(0,1\) 都出现了 \(m\) 次，对应 \(k=m\)，其方案数为 \(\binom{2m}{m}\)。

否则考虑枚举二者中较多的第 \(m+1\) 次出现位置，则前 \(m+k\) 个需要填 \(m\) 个，\([m+k+2,2m]\) 随便填，然后还需要确定众数是谁（\(m+k+1\) 上填什么），就得到了上式。

P2

\[\sum_{k=0}^n\binom{2k}{k}\binom{2n-2k}{n-k} \]

答案是 \(4^n\)。两个上指标的和是 \(2n\)，两个下指标的和是 \(n\)，看成是平面直角坐标系上从 \((0,0)\) 开始走的路径计数。

把 \(\binom{2k}{k}\) 看成是枚举和 \(y=x\) 的最后一个交点。设 \(m=n-k\)，假设下一步向右走，走到 \(y=2n-x\) 直线上并且不走到 \(y=x\) 上的方案数可以用计算类似卡特兰数的方式计算：

\[\sum_{i=0}^{m-1}\binom{2m-1}{i}-\binom{2m-1}{i-1}=\binom{2m-1}{m-1} \]

第一步也可以向上走，方案数一样，\(2\binom{2m-1}{m-1}=\binom{2m}{m}\)。所以就是任意走 \(2n\) 步的方案数。

P3

\[\sum_{i\geq 0}\binom{x+y+i}{i}\binom{y}{a-i}\binom{x}{b-i} \]

答案是 \(\binom{x+a}{b}\binom{y+b}{a}\)。在两边同时乘一个 \(\binom{x+y}{x}\)。

\[\sum_{i\geq 0}\binom{x+y+i}{x,y,i}\binom{y}{a-i}\binom{x}{b-i}=\binom{x+y}{y}\binom{x+a}{b}\binom{y+b}{a} \]

集合是这样的形式：

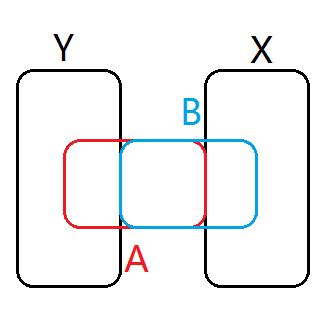
其中 \(\lvert A\rvert=a,\lvert B\rvert=b,\lvert X\rvert=x,\lvert Y\rvert=y,\lvert A\cap B\rvert=i\)，则左式比较平凡，先确定 \(x,y,i\)，各含有多少各元素，然后确定 \(A,B\) 在 \(X,Y\) 中的部分。

若 \(T\subseteq S\)，且对于 \(i\in[1,\lvert T\rvert]\)，确定了在 \(T\) 中第 \(i\) 大的元素在 \(S\) 中是第几大，则称确定了信息 \((T,S)\)。

右式相当于确定了信息 \((X,X\cup Y),(B,X\cup A),(A,Y\cup B)\)，至于要证明通过这三组信息可以确定一个全序关系（即可以排序所有元素）。

考虑每次寻找最小的元素。首先根据 \((X,X\cup Y)\) 中的信息，可以确定最小值一定不在 \(X\) 或者 \(Y\)。假设不在 \(Y\)（不在 \(X\) 同理）：

若 \(X\cup A\) 的最小值在 \(B\) 中，那么若 \(Y\cup B\) 的最小值在 \(A\) 中，则最小值就在 \(A\cap B\) 中，否则在 \(B\setminus (A\cap B)\) 中。

否则在 \(X\setminus B\) 中。

上面这一过程没有信息的浪费（？？？），所以映射是单的。

P4

\[\sum_{k=0}^n\binom n k^2x^k=\sum_{k=0}^n\binom{2n-k}{n-k,n-k,k}(x-1)^k \]

右式可以变成 \(\binom n k\binom{2n-k} n(x-1)^k\)。

左式的组合意义是：\(S,T\subseteq [n],\lvert S\rvert=\lvert T\rvert,f:S\rightarrow[x]\) 的元组 \(A:(S,T,f)\) 数量。

右式的组合意义是 \(S\subseteq[n],T\subseteq[2n]\setminus S,\lvert T\rvert=n,f:S\rightarrow [x-1]\) 的元组 \(B:(S,T,f)\) 数量。

建立双射 \(F:A\rightarrow B\)：

对于左式中的 \((S,T,f)\)，构造 \(S'=\{y\in S|f(y)!=x\},f'(x)=f(x),T'=\{y\in[n]|y\notin S\}\cup(n+T)\)。注意到因为 \(a\in S'\) 中不含 \(f(a)=x\) 的 \(a\)，所以映射 \(f'\) 合法。显然 \(\lvert T'\rvert=n\)。

这种映射对于不同的 \(A\)，显然会映射到唯一的 \(B\)。

\(F':B\rightarrow A\)：

对于右式中的 \((S,T,f)\)，构造 \(T'=\{x-n|x\in T,x>n\}\)，\(S'=[n]\setminus T\)，\(f'(a)=\begin{cases}f(a)\;\; a\in S \\ x\qquad a\notin S\end{cases}\)，这样仍然只会映射到唯一的 \(A\)。

P5.1

\(A\) 是 \(n\) 的有序划分，求：

\[\sum_{A\;\text{is}\;\text{valid}}\prod_{j=1}^ka_j \]

答案是 \(F_{2n-1}\)，\(F\) 是斐波那契数列。

考虑画出 \(n\) 个圆圈，每两个圆圈中间画一个点，共 \(2n-1\) 个元素，然后选择 \(2n-1\) 个元素的一个子集，使得 第一个选的和最后一个选的都是圆圈，并且每两个选择的圆圈间恰有一个点被选择。

这样一个点就代表一个隔板，把 \(n\) 分隔成了若干份，每一份有 \(a_i\) 个圆圈，每个要段中要再选一个，贡献就是乘起来。

可以等价于把 \(2n-1\) 分成若干个 \(1,2\)，选择所有大小为 \(1\) 的块包含的元素，就是斐波那契数列。

P5.2

\(A\) 是 \(n\) 的有序划分，求：

\[\sum_{A\;\text{is}\;\text{valid}}\prod_{j=1}^k(2^{a_j-1}-1) \]

答案是 \(F_{2n-3}\)，其中 \(F\) 是斐波那契数列。

首先考虑怎么把 \(2^{a_i-1}-1\) 和划分成 \(1,2\) 的段找到联系。

对于一个 \(a_i\)，考虑把 \(2a_i\) 划分成若干段，每段的长度是 \(1\) 或 \(2\)。满足：

1. 首段长为 \(1\)，末段长为 \(2\)。

2. 设长为 \(1\) 的段有 \(k\) 段，则 \(k\) 是偶数，并且对于 \(1\sim k-1\) 中的每个偶数 \(z\)，第 \(z\) 个 \(1\) 后面也是 \(1\)。

这样的方案数就是 \(2^{a_i-1}-1\)，考虑去掉开头的第一个 \(1\) 和结尾的 \(2\)，然后在最后一个 \(1\) 后面填一个 \(1\)，这样就是有一个长度为 \(2a_i-3+1\) 的段，没相邻两个为一组，每组可以是 \(\{1,1\}\) 或者是 \(\{2\}\)，并且不能全部是 \(\{2\}\)，所以答案就是 \(2^{a_i-1}-1\)。

然后对于一个数，考虑把所有 \(a_i\) 的拆分段拼起来形成一个和为 \(2n\) 的 \(1,2\) 序列。因为开头的 \(1\) 和末尾的 \(2\) 是固定的，所以方案数是 \(F_{2n-3}\)。

现在证明每一个序列都对应唯一的划分方式。首先 \(1\) 的总个数一定是偶数。执行这样一个过程：从前向后，不断找到满足下一位是 \(1\) 并且前面的 \(1\) 的个数是偶数的第一个 \(2\) 并作为一个划分的结尾。

P6（模拟赛题）

求

\[f(n)=\sum_{m=0}^n\sum_{k=m}^n\binom k m\binom{k-m}{\lfloor\frac{k-m} 2\rfloor}2^{n+m-k} \]

要求 \(\mathcal O(n)\)

整理一下式子：

\[\sum_{k=0}^n2^{n-k}\sum_{m=0}^k\binom k m\binom{k-m}{\lfloor\frac {k-m} 2\rfloor}2^m \]

问题转为求后半部分 \(g(n)=\sum_{m=0}^n\binom n m\binom{n-m}{\lfloor\frac {n-m} 2\rfloor}2^m\)。

考虑 \(S=[2n+1]\) 中 \(1\) 和 \(2\) 匹配，\(3\) 和 \(4\) 匹配 \(\dots\) \(2k-1\) 和 \(2k\) 匹配（\(k\leq n\)），\(2n+1\) 没有匹配。

对于 \(x\leq 2n\) 记 \(x\) 的匹配为 \(m(x)\)。

选取 \(T\subseteq S\) 使得 \(\lvert T\rvert=n\)。对于每种方案，记 \(R=\{x|x\in T,x\not= 2n+1,m(x)\notin T\}\)，设 \(\lvert R\rvert=k\)，则 \(T\) 内部有 \(\frac{n-k} 2\) 对匹配。这样就有了组合意义：

先确定 \(n\) 对匹配中 \(k\) 个恰好只被选入一个到 \(T\) 中，并且决定是哪个被选入，方案数是 \(\binom n k 2^k\)。

剩下的部分还要选 \(\lfloor \frac{n-k}{2}\rfloor\) 对匹配，方案数是 \(\binom{n-k}{\lfloor \frac{n-k}{2}\rfloor}\)。

然后如果 \(n-k\) 是奇数，就把 \(2n+1\) 选进去，否则不选，这样集合大小一定能凑成 \(n\)。所以答案就是 \(g(n)=\binom{2n+1}{n}\)。预处理组合数，预处理前缀和可以做到 \(\mathcal O(n)\)。