NOIP BCT

Day 1

被 ly 干碎。

T1 矩乘，带一个常数 1 和答案总和即可。

T2 等价于找两个相同的子序列并且第一个的结尾位置小于等于第二个的开头位置。枚举第二个的开头位置 \(j\)，设 \(f_{k,a,b}\) 表示分别以 \(a,b\) 结尾的长度为 \(k\) 的子序列有多少个，二维前缀和优化转移可以做到 \(\mathcal O(n^4)\)。发现可以不枚举 \(k\)，\(f_{a,b}\) 表示以 \(a,b\) 结尾的对数，\(g_{a,b}\) 表示以 \(a,b\) 结尾的长度和，转移方程：

\[\begin{aligned} f_{a,b}=\sum_{x=1}^{a-1}\sum_{y=j}^{b-1}f_{x,y}\\ g_{a,b}=f_{a,b}+\sum_{x=1}^{a-1}\sum_{y=j}^{b-1}g_{x,y}\\ \end{aligned} \]

同样可以用二维前缀和优化到 \(\mathcal O(n^3)\)。

T3 咕咕咕

T4 很厉害的题。设 \(dp_i\) 为合法的路径数，显然：

\[dp_i=\sum_{j<i\wedge j\in from_i\wedge col_j\ne col_i}+1 \]

只关心奇偶性，发现异色偶点和同色点是没有影响的，可以随便连，我们只关心异色奇点和该点连边数的奇偶性。如果连了奇数条边，则该点为偶点，否则为奇点。

所以可以设 \(f_{a,b,c,d}\) 表示红色偶点 \(a\) 个，红色奇点 \(b\) 个，黑色偶点 \(c\) 个，黑色奇点 \(d\) 个，以该点为红偶点为例，转移方程如下：

\[f_{a+1,b,c,d}=f_{a,b,c,d}2^{a+b+c}\sum_{j\%2=1}\binom{d}{j} \]

变形一下：

\[f_{a+1,b,c,d}= \begin{cases} 0\quad\quad\quad\quad\quad\quad\quad\;\; d=0\\ f_{a,b,c,d}2^{a+b+c+d-1}\quad d>0 \end{cases} \]

然后就发现和 \(a,b,c,d\) 实际取值无关，只和 \(a+b+c+d\) 以及 \(b,d\) 是否为 \(0\) 有关。状态可以直接记成 \(f_{i,0/1,0/1,0/1}\) 表示前 \(i\) 个点，是否有红色奇点，是否有黑色奇点，当前总路径条数奇偶性，转移方程也比较平凡，和上面一样。

T4 看似非常逆天，完全不可做，第一眼似乎只能想到状压和爆搜，但是经过理性的一步步分析，发现状态可以记录的非常简洁。真的就像沙东一哥 dwt 说的：顺着做就做出来了。但其实场上看到这个题的第一眼已经丧失了挑战它的勇气/lh/lh。

Day 2

被 ly 干碎。

T1 快速幂然后随便做。

T2 双指针+树状数组求逆序对即可。我是 SB，开始没把左端点右移，疯狂挂分。

T3 等价于重心。以重心为根，这是一个点子树内一定满足要求，字数外用值域线段树维护能删那些子树的 \(siz\)，线段树上二分。另一种 corner case 是直接把重心接到这个点上然后从重心上删子树，和答案取 \(\min\) 即可。

T4 在 LCA 处统计 \(dep\)，每个子树内只关心跳出来了多少次，不关心内部怎么跳的。设 \(f_{i,j}\) 表示 \(i\) 子树内有 \(j\) 个连续段。合并子树的转移方程：

\[f_{x,k}=\sum_{i=0}^{siz_x}\sum_{j=max(0,k-i)}^{siz_to}f_{x,i}f_{to,j}g_{i,j,k} \]

\(g_{i,j,k}\) 表示 \(i\) 条和 \(j\) 条线段拼成 \(k\) 条的方案数。还是计数 DP 基本思路，考虑第一个线段有几个 \(i\)，此时一定有 \(j=i-1,i,i+1\)，只枚举 \(i\) 即可。

\[g_{i,j,k}=2\times\sum_{t=0}^{min(i,j)}g_{i-t,j-t,k-1} \sum_{t=0}^{min(i,j-1)}g_{i-t,j-t-1,k-1} \sum_{t=0}^{min(i-1,j)}g_{i-t-1,j-t,k-1} \]

复杂度 \(\mathcal O(n^4)\)，前缀和优化到 \(\mathcal O(n^3)\)。

Day 3

被 ly 干碎。

T1 行列连边，看是否是 DAG 即可。

T2 神奇计数，赛时推的式子极其麻烦，实际上可以十分优雅的推出来。

\(m\) 个数里选 \(n-1\) 个 \(\binom{n}{m-1}\)（一共 \(n\) 个，两个相同），找一个相同的（不能是最大的） \(\times m-2\)，最大值 \(\times n\)，其余的任意分配位置 \(2^{n-3}\)。

T3 容斥 DP，设 \(f_{i,j}\) 表示考虑 \(i\) 种数字至少不合法 \(j\) 个的容斥系数乘方案数。

转移方程 \(f_{i,j}=\sum_{k=1}^{siz_i}f_{i-1,j-k}(-1)^k\binom{siz_i}{k}\)。

注意到最后剩下的是一个多重集排列数，答案是 \(f_{i,j}j!\)，但是这是不考虑同样的数字的情况。所以前面需要除去这个贡献。

转移方程 \(f_{i,j}=\sum_{k=1}^{siz_i}f_{i-1,j-k}(-1)^k\binom{siz_i}{k}\dfrac{1}{(siz_i-k)!}\)。

复杂度 \(\mathcal O(n^2)\)。

T4 '(' 为 \(1\)，')' 为 \(-1\)，等价于全局和为 \(0\) 切任意前缀和非负，线段树维护区间 \(sum\) 和区间 \(\min\) 即可。

Day 4

ly 被干碎/cf/cf。

T1 难点在于读题。先加一次 \(\dfrac{L+1}{2}\)，再加 \(\dfrac{L+3}{2}\)，然后一定是一边加 \(2\) 一边加 \(2\)。赛时忘了特判 \(0\)，-10/kk/kk。

T2 有意义的只有只有一个质因子的数。一一匹配一定是最优的，此时只有一种情况：区间存在绝对众数。开一个线段树维护区间绝对众数，另一个动态开点线段树或者平衡树或者主席树维护区间值的个数来 \(check\)，复杂度 \(\mathcal O(n\log n)\)。

T3 边双内部的点一定互相可达，缩点成一棵树然后树剖线段树区间覆盖 01 即可。

T4 析合树。

评价是，只强制了，没有在线。ans 为什么永远都是 \(0\)？？？/cf/cf/cf/cf/cf，-70，痛失 rk1。

另一种做法：类似全局连续段，扫描右端点，类似比赛，点上维护 \(\max_i^ra_i-\min_i^ra_i-r+l\) 维护区间历史 \(0\) （这是最值）的个数。强制在线的话主席树。历史历史和，比较逆天。

Day 5

ly 又被干碎/cf/cf。

T1 打表发现有贡献的位置是有规律的，设 \(f_{i,j}\) 为区间答案，\(len=j-i+1\)，\(f_{i,j}=f_{i,i+len-highbit(len)-1}\oplus f_{j-(len-highbit(len))+1,j}\)，可以先 \(\mathcal O(n^2)\) 求出来一个区间的答案，然后 \(\mathcal O(n^2)\) 做一下类似前缀和的东西，最后 \(\mathcal O(1)\) 查询。

T2 淀粉，统计一颗子树对其他子树的贡献，对于覆盖了全部点的首都直接记下全局贡献。答案为 \(\sum_{j=dep_i}^{maxdep}i\times cut_i+val_i\)，\(cut_i\) 表示 \(v_j-depth_j=i\) 的点的个数，\(val_i\) 表示贡献。最后自己对自己的贡献减回去，复杂度一只 \(\log\)。

T3 神奇 DP。首先一定是小的并到大的上，并且最大的一定不动。把 \(a\) 从大到小排序，把合并抽象成一棵树，表示子节点并到了父节点上，花费为 \(dep_i\times a_i+2^{deg_i}-1\)。直接爆搜或者直接 DP 复杂度很劣，推一推性质（此处度数指子节点数）：

1. 同一层内度数只差不超过 \(1\)，否则显然可以把度数多的移到度数少的上更优秀。
2. 层数少的层的点的最小度数不低于层数多的层的最大度数，否则可以把一颗子树上移减少答案。

有了这两条重要性质，就可以直接 DP。设 \(f_{i,j,k,l}\) 表示当前层最后一个节点是 \(i\)，在第 \(j\) 层，上一层有 \(k\) 个点，本层有 \(l\) 个点。\(s\) 表示 \(a\) 的前缀和，转移方程是简单的：

\[\begin{aligned} deg&=l/k\\ f_{i+xt+(l-t)(x-1),j+1,l,degt+(l-t)(deg-1)}&=\min_{x=1}^{deg}\min_{t=1}^{l}f_{i,j,k,l}+t\times (2^x-1)+(l-t)\times (2^{x-1}-1)+(s_{i+xt+(l-t)(x-1)}-s_i)j \end{aligned} \]

发现复杂度仍然过高。但是 \(j\) 其实是可以用费用提前计算的思想优化掉。

\[\begin{aligned} deg&=l/k\\ f_{i+xt+(l-t)(x-1),l,degt+(l-t)(deg-1)}&=\min_{x=1}^{deg}\min_{t=1}^{l}f_{i,j,k,l}+t\times (2^x-1)+(l-t)\times (2^{x-1}-1)+s_n-s_i \end{aligned} \]

理论好像是 \(\mathcal O(n^5)\)，但是常数奇小无比，剪剪枝，DP 值过大就不转移就过了/lh/lh。

T4 不会。

wzm 怎么 AK 了/jk/jk。

Day 6

ly 噶了。

T1 简单差分，第一种操作就是只考虑 \(delta>k\) 的差分值，对正负和取 \(\max\)。第二种由于正负和相等，直接取正的和为答案。

T2 有点，太逆天了。只会 \(\mathcal O(n)\)。等价于一个数不同的质因子个数是奇数的数目。设 \(f_i=1\) 表示为奇数，\(f_i=0\) 表示为偶数。要求的是这个东西的前缀和。可以欧拉筛。

T3 我爱淀粉，淀粉使我快乐。（虽然又被 wqy 嘲讽，虽然一只 \(\log\) 跑不过 BIT 加树剖两只 \(\log\)/ll/ll/ll）。建出淀粉树，修改就是以所有祖先节点为中转节点，不需要额外的数据结构，只需要记录两个 tag，一个表示需要减 \(tag1*dis(i,root)\)，另一个表示需要减 \(tag2\)，然后发现会算重，在加两个 \(tag\) 表示减去父节点的贡献的值即可。复杂度 \(\mathcal O(n\log n)\)。

T4 咕咕咕。

Day 7

ly 之后几天都噶了/lh。

是谁 4 题都会挂了 230 昏呢？？？

T1 森林直径。

T2 gcd 只会变化 \(\log V\) 次的性质可以做到 \(\mathcal O(n\log V)\)，有平凡的双 \(\log\) 做法，st 表+二分等。出题人想卡似乎没卡掉/jy。忘了判右端点可以取到 \(n\)，-100。

T3 比较有意思。等价于求存在绝对众数的子区间个数。重要性质：一个区间最多只有一个绝对众数，枚举绝对众数，设 \(sum_i\) 表示前缀有多少个数等于当前枚举的绝对众数，此时 \([j+1,i]\) 合法的充要条件是 \(2(sum_i-sum_j)>i-j\)，化简一下，\(2sum_j-j<2sum_i-i\)，对于每个颜色 \(\mathcal O(n\log n)\) 树状数组维护 \(=sum_i-i\) 的数的个数的前缀和，这样最坏复杂度仍然 \(\mathcal O(n^2\log n)\)。

发现所有等于这个颜色的值的数的数量级是 \(\mathcal O(n)\)，考虑如何只考虑等于当前颜色的位置。发现 \(2*sum_i-i\) 的图像是这样的：

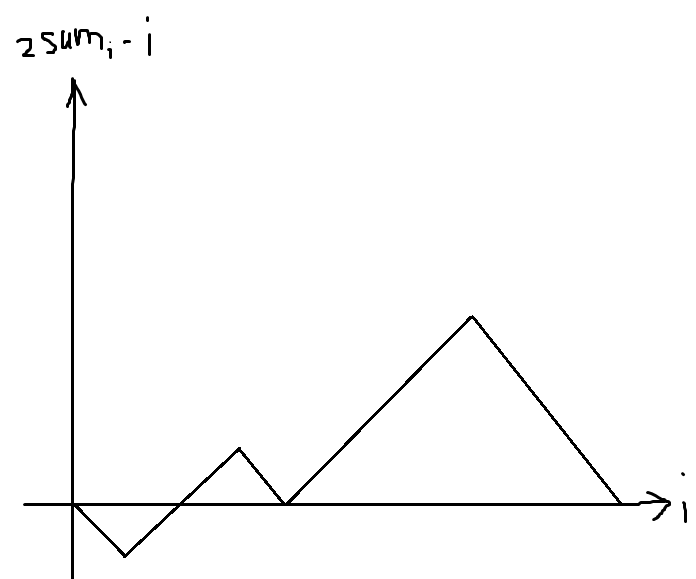
由一些折线组成，斜率为 \(1\) 表示该位置是这个颜色，否则不是。但是对于所有颜色的所有折线，折线的数量级是 \(\mathcal O(n)\) 的，所以对于一条折线一起处理。需要查询的是区间前缀和之和，操作是区间加。在做一下前缀和变成：区间和，区间加等差数列，区间加，线段树维护即可。也可以大力差分树状数组维护 \(sum,sum\times i,sum\times i^2\) 的前缀和，结果线段树跑 10s+，BIT 跑 1s+ /lh/lh/lh。

vector =n的颜色忘了扔进去一个 \(0\)，导致颜色互不相同是答案是 \(n\) 我输出了 \(n-1\)，-30。

T4 容斥。总方案数是 \(K^{n-1}\)，减去不合法的方案数，即至少有一条路径颜色全部相同。可以 \(2^n\) 枚举子集，然后乘上容斥系数。方案数可以用并查集把边缩成一些连通块，最后统计连通块个数 \(m\)，方案就是 \(K^m\)。复杂度 \(\mathcal O(n2^n\alpha n)\)。

文件打错，-100。

总体评价：全体目光向我看齐，看我看我啊，我宣布个事，我是个 SB！！

Day 8

T1 爆搜。读错题，-70。

T2 预处理关键点间两两最短路，\(f_{i,S}\) 表示当前还未经过 \(S\) 中的位置，当前在 \(i\) 走到 \(n\) 的期望。如果有车一定直接骑到 \(n\)，否则对还未走到的其他点的 DP 值和距离和取 \(\min\) 即可。样例 2 锅了，我不知道，虚空调试 1h+。

T3 咕咕咕。

T4 咕咕咕。

Day 9

竟然是 lxl 题/jy/jy/jy。非常好比赛，使我的 rating 增长，爱来自沙东的青蛙。

T1 二分答案套二分查找。需要稍微卡卡常。

T2 暴力枚举 \(a\)，发现答案就是 \([(n^2+1)%a,(n^2+1)%a+p]\) 中在 \([m,P]\) 中的因子数，预处理即可。输出前 \(100000\) 个直接暴力处理。

T3 得分是好求的。把 \(A,B\) 从小到大排序，\(A\) 从后向前扫，尽量找比它大的 \(B\)，找不到就不找，这样可以预处理出一些有贡献的 \(a\)。然后再求一遍使得 \(a\) 对应的 \(b\) 尽量小。这样我们把大的 \(b\) 保留下来，以后再分配到尽量小的位置，这样贪心是对的，可以用决策包容性证明，即当前状态到达的下一个状态包含了原先的状态，一定不会劣于原先答案。

然后按照 \(A\) 的下标从前向后扫，设 \(ans_i\) 表示位置 \(i\) 对应的 \(B\) 的值。用一个 multiset 存当前 \(B\) 中没用被用过的值，再开一个 multiset 存所有的 \(ans_i\)。

此时一定是在不改变得分的情况下能用多大的数用多大的数。如果当前 \(ans_i\) 不为 \(0\) 即它是之前的候选项，则直接选一个最大的把它覆盖掉。这里能选的是它原来的 \(ans_i\) 和第一个集合中最大的数。若当前 \(ans_i\) 为 \(0\) 说明它原来不是候选项。这时不能随便用第二个集合中的数，需要判一下是否合法。因为把第二个集合中的数拿走可能导致得分减少，必须保证这个位置是得分的，所以需要 check 一下。但是这样可能导致 \(ans_i\) 不为 \(0\) 并且在集合二中找不到它，还是需要特判，比 sol 做法好写 114514 倍。

T4 太厉害了。一眼二分答案，发现判定非常不好搞因为要确保不能砸到 \(<0\)，而且手玩发现直接贪心砸最高的是错的。原因是可能等一等竹子长得更高这样砸一次收益更大。所以可以考虑反着做：一开始高度都为 \(mid\)，每天会下降 \(a_i\)，操作是拔高 \(t\)，要求最后低于 \(h_i\) 且任意时刻不能 \(<0\)。开一个堆，权值是每个竹子在第几天落到 \(<0\)，这样每次选最大的 \(k\) 个拔高就行了。反着做的本质是便于处理贪心策略。复杂度 \(\mathcal O((n+mk)\log n\log V)\)。

好不容易 AK 一场，线下的忘记开文件了，-100/fn/fn/fn。

总榜 rk4，但是 ly 不噶的话肯定是干不过的/fad。