P4099 [HEOI2013] SAO
很有意思的一道题。
考虑树形 DP。首先考虑的是 \(f_i\) 表示 \(i\) 为根的子树内合法的拓扑序数量，但是这样合并子树的时候是无法计算的，如下图：
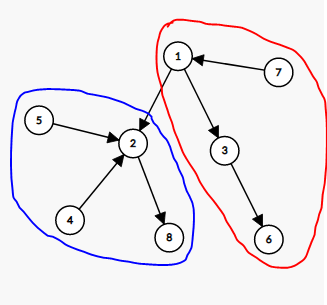
假设 \(1\) 当前合并了 \(3\) 这棵子树，接下来要合并红色和蓝色的部分，此时 \(2\) 必须在 \(1\) 之后挑战，但是方案数并不是简单地两个 \(f\) 值相乘，观察可以发现 \(5,4,7\) 号点的合并顺序是任意的，并且 \(1,2\) 都挑战了之后 \(3,6,8\) 的挑战顺序也不是一种，所以我们合并的时候会乘两个神秘系数。
观察性质，合并 \(i,to\) 两棵树时，问题可以抽象为两个序列，合并之后 \(i\) 需要在 \(to\) 前面并且保持原先相对顺序不变，而上面所说的的神秘系数其实完全由在 \(i,to\) 之前与之后的数的个数决定。
注意到我们并不关心前面的数的顺序，因为这个东西显然满足乘法原理，只需要把顺序数存在 \(f\) 里直接乘起来就是对的。
很自然的，想到再加一维状态 \(f_{i,j}\) 表示 \(i\) 在它当前子树内排名为 \(j\) 的方案数（本质上还是记录的在它之前的数的个数 \(j-1\)，而在它之后的数就是 \(siz_i-j\)），接下来是愉快的推式子时间：
设 \(i,to\) 为当前合并的两棵树，其中 \(i\) 在它所在的子树内排在第 \(j\) 位，\(to\) 在它所在的子树内排在第 \(k\) 位。
若 \(i\) 指向 \(to\)，即 \(i\) 在 \(to\) 之前挑战，则合并大概是这样的：
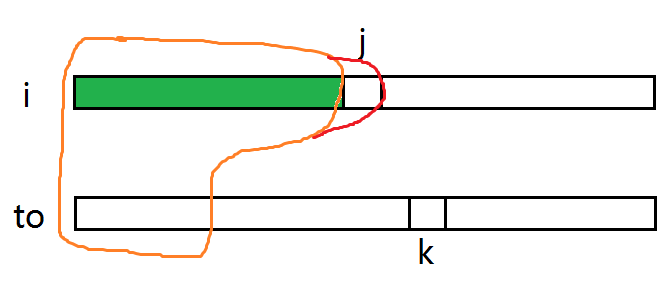
橙圈表示合并后的序列在 \(i\) 之前的数字数，枚举 \(t\) 表示合并后 \(i\) 的位置在第 \(t\) 位，则红圈一定是第 \(t\) 个，橙圈中应当有 \(t-1\) 个数，其中 \(j-1\) 个为序列 \(i\) 中的元素，合并顺序随意，所以第一个系数就是 \(C_{t-1}^{j-1}\)。
新序列中第 \(t\) 个为数字是 \(i\)，接下来 \(siz_i+siz_to-t\) 个数中有 \(siz_i-j\) 个是序列 \(i\) 中的元素，所以第二个系数就是 \(C_{siz_i+siz_to-t}^{siz_i-j}\)。
对于 \(t\) 的取值，最少取 \(j\)，最多取 \(j+k-1\)，因为 \(to\) 一定在 \(i\) 之后，如果 \(t>j+k-1\) 则一定是合法。
整理一下，在外层枚举 \(t\)，求出 \(k\) 的取值范围 \([1,t-j+1]\) 就得出转移方程：
观察一下，其中只有 \(f_{to,k}\) 一项中包含 \(k\)，并且是连续的一段，显然可以用前缀和优化。
对于 \(to\) 指向 \(i\) 的情况也是同理，转移方程甚至也是一样的，只不过取值变了一些。
最后讨论一下时间复杂度，对于每一条边连接 \(fa_x\) 和 \(x\)，它会被计算 \((siz_{fa_x}-siz_x)siz_x\)，相当于是把它两边的点互相枚举了一遍，这样每个点对只会合并一次，所以时间复杂度是优秀的 \(\mathcal O(n^2)\)。
本题无论是状态的设计，方程的推导，范围的计算，转移的优化都需要细致的思考，是一道不可多得的好题。
int T,n,cnt,fr[1001],inv[1001],head[1001],to[2001],nex[2001],v[2001],tmp[1001],f[1001][1001],siz[1001];
inline void add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
inline int C(int n,int m){return fr[n]*inv[m]%MOD*inv[n-m]%MOD;}
inline int power(int x,int y)
{
int s=1;
for(;y;y>>=1,x=x*x%MOD)if(y&1)s=s*x%MOD;
return s;
}
void dfs(int x,int fa)
{
siz[x]=1,f[x][1]=1;
for(int i=head[x];i;i=nex[i])
{
if(to[i]==fa)continue;
dfs(to[i],x),memcpy(tmp,f[x],sizeof(tmp)),memset(f[x],0,sizeof(f[x]));
if(v[i]==1)
{
for(int j=1;j<=siz[x];++j)
{
for(int t=j;t<=j+siz[to[i]]-1;++t)
f[x][t]=(f[x][t]+tmp[j]*((f[to[i]][siz[to[i]]]-f[to[i]][t-j])%MOD+MOD)%MOD*C(t-1,j-1)%MOD*C(siz[x]+siz[to[i]]-t,siz[x]-j))%MOD;
}
}
else
{
for(int j=1;j<=siz[x];++j)
{
for(int t=j+1;t<=siz[to[i]]+j;++t)
f[x][t]=(f[x][t]+tmp[j]*f[to[i]][t-j]%MOD*C(t-1,j-1)%MOD*C(siz[x]+siz[to[i]]-t,siz[x]-j))%MOD;
}
}
siz[x]+=siz[to[i]];
}
for(int i=2;i<=siz[x];++i)f[x][i]=(f[x][i]+f[x][i-1])%MOD;
}
inline void mian()
{
fr[0]=inv[0]=1,read(T);int x,y;char ch;
for(int i=1;i<=1000;++i)fr[i]=fr[i-1]*i%MOD;
inv[1000]=power(fr[1000],MOD-2);
for(int i=999;i>=1;--i)inv[i]=inv[i+1]*(i+1)%MOD;
while(T--)
{
read(n),memset(head,0,sizeof(head)),memset(f,0,sizeof(f)),cnt=0;
for(int i=1;i<n;++i)read(x),ch=getchar(),read(y),++x,++y,add(x,y,ch=='<'),add(y,x,ch=='>');
dfs(1,0),write(f[1][n],'\n');
}
}
