[DDCC2020D] Pars/ey
重工业题。
找环然后树形 DP 是显然的,先考虑断开环上的边怎么做。
把环复制一遍放在结尾,记 \(sum_i\) 为环长的前缀和,\(f_i\) 为该子树内的最长根链的长度,问题变为每次给定一个区间,要求找到 \(i,j(i>j)\) 使得 \(sum_i-sum_j+f_i+f_j\) 最大,可以使用线段树实现。注意要与同一棵树里的直径取 max(大概有 \(\mathcal O(n)\) 做法吧)
然后考虑树边如何处理。先求出不删边时基环树的直径,如果是树内的直径那么删其他边不会对答案造成影响,所以只需计算该子树。直径经过了环可以对两个端点所在的树计算两次。
断了树边后基环树的直径有 2 种情况:直径至少有一端在这棵树里和不在这棵树里。两端都在树外面是好处理的,对于第一种情况可以类似换根的方法处理。
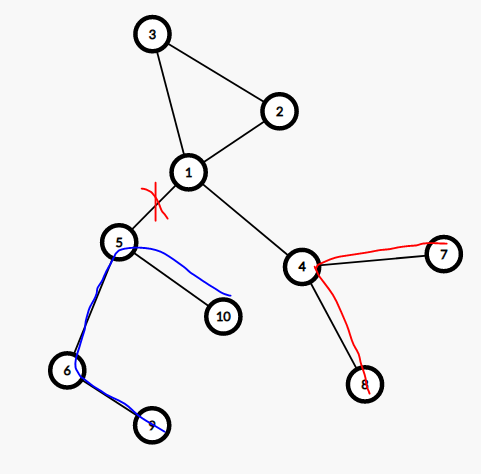
1.直径为蓝色或红色的路径。
蓝色的路径是好处理的,对于每棵子树维护子树内直径即可。
对于红色,因为换根到儿子时红色路径的长度可以继承父亲的,所以只需要一个变量记录当前红色路径的长度。
设当前最长的红色路径长度为 \(dead\),设 \(in_{k,0}\) 表示以 \(k\) 为根的子树内不经过该点的最大直径, \(in_{k,1}\) 表示和 \(in_{k,0}\) 不在同一棵子树里的最大直径,这样向下搜索时如果 \(to\) 是 \(in_{k,0}\) 所在的子树,用 \(in_{k,1}\) 更新 \(dead\),否则用 \(in_{k,0}\) 更新。
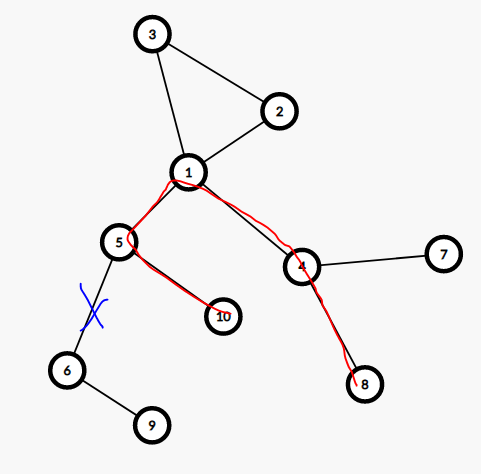
另一种情况,如下图:这条红色路径的可以在 \(5\) 号点是更新,具体的,类似换根 DP 的思路,我们记 \(maxn\) 表示当前点向父亲走能走到的最远的距离(树内),用 \(maxn+f_k\) 更新红色路径的长度。但是更新时会出现问题:\(f_5\) 本身由 \(f_6\) 转移而来,所以我们不仅要记录最长根链的长度,还要记录和最长根链不在同一子树内的次长根链的长度,如果 \(f_{to,0}+v_i\) 和 \(f_{k,0}\) 相等,用 \(f_{k,1}+maxn\) 更新红色路径,否则用 \(f_{to,0}\) 更新。
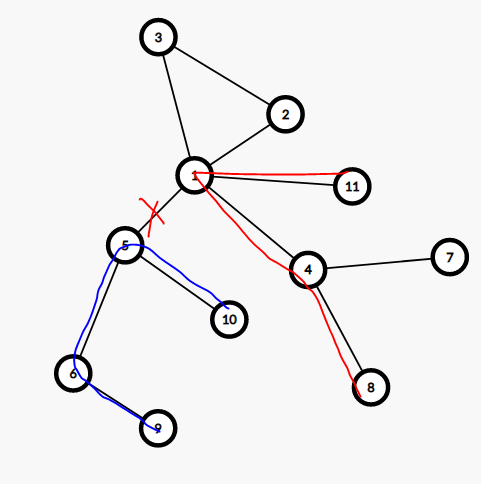
另另一种情况,如下图:断掉了 \((1,5)\),\(dead\) 还可以由 \(1\) 子树内不经过 \(5\) 的两条链拼接而成,所以我们不仅要记录次大根链,还要记录次次大根链,如果断的边是 \(f_{k,0}\) 的链,用 \(f_{k,1}+f_{k,2}\) 更新 \(dead\),其他情况同理。
2.直径另一端不在该树内。
这种情况是 trival 的,记录 \(up\) 表示该点到根的距离,每次向下走维护到根的距离的最大值和当前到根的距离,每次还是判断最大次大值与子树的值的关系即可。
细节很多,非常难写。
int n,cnt=1,dead,tot,max2,all,now,now2,maxu,maxi,maxj,ans[800001],pos[800001],id[800001],ide[800001],in[800001][2],f[800001][3],ex[800001],vis[800001],loop[800001],head[800001],to[800001],nex[800001],v[800001],sum[800001],val[800001];
inline void add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
stack<int> st;
namespace Segment
{
struct Node{int maxn,max1,max2,l,l1,r,r2;};
struct{int l,r;Node nd;}t[3400001];
Node operator +(const Node nd1,const Node nd2)
{
Node nd;nd.l=nd1.l1,nd.r=nd2.r2,nd.maxn=nd1.max1+nd2.max2;
if(nd1.maxn>nd.maxn)nd.maxn=nd1.maxn,nd.l=nd1.l,nd.r=nd1.r;
if(nd2.maxn>nd.maxn)nd.maxn=nd2.maxn,nd.l=nd2.l,nd.r=nd2.r;
if(nd1.max1>nd2.max1)nd.l1=nd1.l1;else nd.l1=nd2.l1;nd.max1=max(nd1.max1,nd2.max1);
if(nd1.max2>nd2.max2)nd.r2=nd1.r2;else nd.r2=nd2.r2;nd.max2=max(nd1.max2,nd2.max2);
return nd;
}
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r;
if(l==r)return t[p].nd.l=t[p].nd.l1=t[p].nd.r=t[p].nd.r2=l,val[l]+=val[l-1],t[p].nd.max2=f[loop[l]][0]+val[l-1],t[p].nd.max1=f[loop[l]][0]-val[l-1],void();
int mid=l+((r-l)>>1);
build(p*2,l,mid),build(p*2+1,mid+1,r),t[p].nd=t[p*2].nd+t[p*2+1].nd;
}
void change(int p,int x,int y)
{
if(t[p].l==t[p].r)return t[p].nd.max2=y+val[x],t[p].nd.max1=y-val[x],void();
if(x<=t[p*2].r)change(p*2,x,y);else change(p*2+1,x,y);
t[p].nd=t[p*2].nd+t[p*2+1].nd;
}
Node ask(int p,int l,int r)
{
if(l<=t[p].l&&r>=t[p].r)return t[p].nd;
if(l>t[p*2].r)return ask(p*2+1,l,r);
if(r<=t[p*2].r)return ask(p*2,l,r);
return ask(p*2,l,r)+ask(p*2+1,l,r);
}
void print(int p)
{
if(!t[p].l)return;
write(t[p].l),write(t[p].r),write(t[p].nd.max1),write(t[p].nd.max2),write(t[p].nd.maxn,'\n');
print(p*2),print(p*2+1);
}
}
using namespace Segment;
void findloop(int k,int from)
{
st.e(k);
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1))continue;
if(sum[to[i]])
{
int y;sum[k]=v[i],ide[k]=i;
do vis[loop[++tot]=y=st.top()]=1,id[tot]=ide[y],val[tot]=sum[y],st.pop();while(y!=to[i]);
}
else sum[k]=v[i],ide[k]=i,findloop(to[i],i);
if(tot)return;
}
st.pop();
}
void dfs(int k,int from)
{
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1)||vis[to[i]])continue;
dfs(to[i],i);int tmp=max(in[to[i]][0],f[to[i]][0]+f[to[i]][1]);
if(tmp>=in[k][0])in[k][1]=in[k][0],in[k][0]=tmp;
else if(tmp>=in[k][1])in[k][1]=tmp;
if(f[to[i]][0]+v[i]>=f[k][0])f[k][2]=f[k][1],f[k][1]=f[k][0],f[k][0]=f[to[i]][0]+v[i];
else if(f[to[i]][0]+v[i]>=f[k][1])f[k][2]=f[k][1],f[k][1]=f[to[i]][0]+v[i];
else if(f[to[i]][0]+v[i]>=f[k][2])f[k][2]=f[to[i]][0]+v[i];
}
}
inline void dfs2(int k,int maxn,int from,int up)
{
int pre=maxu,ppr=dead;
// write(k),write(dead,'\n');
for(int i=head[k],upon;i;i=nex[i])
{
if(vis[to[i]]||i==(from^1))continue;
if(in[to[i]][0]==in[k][0]||f[to[i]][0]+f[to[i]][1]==in[k][0])dead=max(dead,in[k][1]);
else dead=max(dead,in[k][0]);
// write(to[i]),write(in[k][0]),write(in[k][1]),write(dead,'\n');
if(f[to[i]][0]+v[i]==f[k][0])dead=max({dead,f[k][1]+maxn,f[k][1]+f[k][2]});
else if(f[to[i]][0]+v[i]==f[k][1])dead=max({dead,f[k][0]+maxn,f[k][0]+f[k][2]});
else dead=max({dead,f[k][0]+f[k][1],maxn+f[k][0]});
// write(to[i]),write(dead,'\n');
if(f[to[i]][0]+v[i]==f[k][0])upon=f[k][1],maxu=max(maxu,up+f[k][1]),dfs2(to[i],max(maxn,f[k][1])+v[i],i,up+v[i]);
else upon=f[k][0],maxu=max(maxu,up+f[k][0]),dfs2(to[i],max(maxn,f[k][0])+v[i],i,up+v[i]);
ans[pos[i]]=max({dead,in[to[i]][0],f[to[i]][0]+f[to[i]][1],now+max(maxu,upon+up),now2});
if(f[to[i]][0]+v[i]==f[k][0])ans[pos[i]]=max({ans[pos[i]],f[k][1]+f[k][2],f[k][1]+maxn});
else if(f[to[i]][0]+v[i]==f[k][1])ans[pos[i]]=max({ans[pos[i]],f[k][0]+f[k][2],f[k][0]+maxn});
else ans[pos[i]]=max({ans[pos[i]],f[k][0]+f[k][1],f[k][0]+maxn});
maxu=pre,dead=ppr;
}
// write(k),write(dead,'\n');
}
inline Node calc2()
{
Node nd1,nd2;nd1.maxn=0;
for(int i=2,j=1;i<=tot*2;++i)
{
while((val[i]-val[j])*2>all)++j;
nd2=ask(1,j,i);if(nd2.maxn>nd1.maxn)nd1=nd2;
}
return nd1;
}
inline void calc(int ex)
{
if(ex>tot)ex-=tot;
change(1,ex,0),change(1,ex+tot,0),dead=0;
now=-INF,now2=calc2().maxn;
for(int i=1;i<=tot;++i)if(i!=ex)now2=max({now2,in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1]});
for(int i=ex+tot-1;i>ex;--i)if((val[i]-val[ex])*2<=val[tot+1])now=max(now,val[i]+f[loop[i]][0]-val[ex]);
for(int i=ex+1;i<ex+tot;++i)if((val[ex+tot]-val[i])*2<=val[tot+1])now=max(now,f[loop[i]][0]-val[i]+val[ex+tot]);
dfs2(loop[ex],0,0,0);
change(1,ex,f[loop[ex]][0]),change(1,ex+tot,f[loop[ex]][0]);
}
inline void mian()
{
read(n);int x,y,z,pos2=0;Node nd;
for(int i=1;i<=n;++i)read(x,y,z),add(x,y,z),add(y,x,z),pos[cnt]=pos[cnt-1]=i;
findloop(1,0),reverse(loop+1,loop+tot+1),reverse(val+1,val+tot+1),reverse(id+1,id+1+tot),id[0]=id[tot];
for(int i=1;i<=tot;++i)loop[i+tot]=loop[i],val[i+tot]=val[i],now=i,dfs(loop[i],0),max2=max({max2,in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1]}),max(in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1])==max2?pos2=i:0;
build(1,1,tot*2),all=val[tot];
for(int i=tot*2;i>=1;--i)val[i]=val[i-1];
nd=calc2();
for(int i=1;i<=tot;++i)ans[pos[id[i-1]]]=max(max2,ask(1,i,i+tot-1).maxn);
if(nd.maxn<=max2)calc(pos2);else calc(nd.l),calc(nd.r);
for(int i=1;i<=n;++i)if(!ans[i])write(max(nd.maxn,max2),'\n');else write(ans[i],'\n');
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号