P4182 [USACO18JAN] Lifeguards P
P4182 [USACO18JAN] Lifeguards P
提供一个比较优秀大常数的时间 \(\mathcal O(nm)\),空间线性的做法。由于变量名冲突,本文中 \(m\) 均指题目中的 \(k\)。
推推性质,发现若区间包含了另一个区间,则一定删掉被包含的区间,正确性显然。这样我们得到了一些左右端点都递增的线段。
将端点从小到大排序,很自然的设 \(f_{i,j}\) 表示前 \(i\) 个线段扔了 \(j\) 个,并且强制选择 \(i\) 保留,容易列出转移方程:
可以 \(\mathcal O(n)\) 枚举 \(k\),复杂度 \(\mathcal O(n^2m)\)。
观察上式,发现可以分成两个部分。
把 \(f\) 抽象成一个二维的表,发现 \(f_{i,j}\) 的决策集合是第零行的一段前缀与一条在它左边一个单位的斜线。
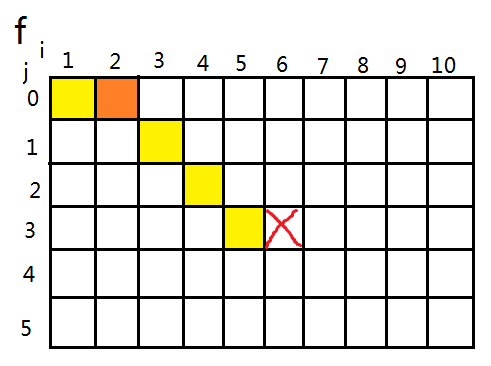
上图中打红叉的格子是当前的 \(f_{i,j}\),黄色的格子是决策集合。
所以我们可以枚举橙色格子的位置,每次处理一条向右下的斜线的所有格子 DP 值这样决策集合是单增不减的,对于第零行首先预处理出 DP 值(第一行表示一个都不删,随便 DP),然后额外维护。
但是现在的问题是如何处理式子右边的两个 \(\max\),记 \(pre_i\) 表示编号最小的和 \(i\) 有重叠部分的线段,这样我们可以把 \(\max\) 再拆开。
注意边界特判。继续观察式子,发现我们需要维护:
-
第 \(0\) 行的前缀的 \(f_{0,i}\) 的最大值。
-
斜线上的前缀 \(f_{i,j}\) 的最大值。
-
第 \(0\) 行的区间 \(f_i-r_i\) 的最大值。
-
斜线上区间 \(f_{i,j}-r_i\) 的最大值。
前两个是好维护的,第四个由于 \(pre_i\) 单增,决策集合右端点和左端点都只增不减,所以可以单调队列,但是第三个我们似乎没有好的处理方式,好像只能 ST 表或者线段树之类的,但是这样除非用一些科技,时间或空间会多一只 \(\log\),我们想要更优秀和更简单的解决方式。
继续观察第三个式子。一条斜线上只有 \(m\) 个点需要 DP,但是注意查询区间的长度是没有限制的,可能许多点的 \(pre\) 都远远小于它本身,只简单的在第 \(0\) 行维护一个单调队列复杂度是假的,最差仍然是 \(\mathcal O(n^2m)\)。
但是发现所以左端点最多只有 \(m\) 个,所以我们可以记录哪些点是其他点的 \(pre\),然后把打了标记的点之间的 \(f_{0,i}-r_i\) 的权值都归到左边的标记点上。这样一条斜线的左端点数就是 \(\mathcal O(m)\) 的级别了。我们只需要在第 \(0\) 行维护另外一个单调队列,每次对于一条斜线预处理出它要查询的位置到当前橙色格子的 \(\max f_{0,i}-r_i\)(点数也是 \(\mathcal O(m)\) 级别的),这样复杂度就是对的。
代码细节很多,很不好写。
int n,m,len,ans,cnt,now,from,real[100001],pre[100001],t[101],pos[100001],Val[100001],V[100001],vis[100001],h[100001],f[2][101];
pii a[100001],b[100001];
bool cmp(pii x,pii y){return x.se<y.se;}
deque<int> Q,q;
inline void mian()
{
read(n,m),from=1;
for(int i=1;i<=n;++i)read(a[i]),--a[i].se;
sort(a+1,a+1+n,cmp),b[0]=mp(-inf,-inf);
for(int i=1;i<=n;++i)
{
while(b[len].fi>=a[i].fi)--len;
b[++len]=a[i];
}
m=max(0,m-(n-len)),n=len,memset(Val,128,sizeof(Val)),memset(f,128,sizeof(f)),h[0]=len=0;
for(int i=1,j=0;i<=n;vis[pre[i++]=j+1]=1)while(b[j+1].se<b[i].fi)++j;
for(int i=1;i<=n;++i)h[i]=h[i-1]+b[i].se-max(b[i-1].se,b[i].fi-1);
for(int i=n,maxn=h[n]-b[n].se;i>=1;--i,maxn=max(maxn,h[i]-b[i].se))if(vis[i])V[pos[i]=++len]=maxn,real[len]=i,maxn=-inf;
for(int i=1;i<=n;++i)if(pos[i])pos[i]=len-pos[i]+1;
reverse(V+1,V+1+len),reverse(real+1,real+1+len);
if(n>=m)ans=h[n-m];
for(int st=1,last=0;st<=n;++st)
{
while(!q.empty())q.pop_back();
now^=1,from^=1;int r=min(last,pos[pre[st+m]]);
while(!Q.empty()&&Q.front()<real[r])Q.pop_front();
if(Q.size())
Val[r]=h[Q.front()]-b[Q.front()].se;
else
Val[r]=-inf;
for(int i=r-1;i>=pos[pre[st]];--i)
Val[i]=max(Val[i+1],V[i]);
for(int i=st+1,j=1,maxn=0,i1=i-2,j1=0;i<=n&&j<=m;++i,++j)
{
f[now][j]=h[min(st-1,max(0,pre[i]-1))]+b[i].se-b[i].fi+1;
f[now][j]=max(f[now][j],b[i].se+Val[pos[pre[i]]]);
while(i1+1<pre[i]&&i1+1<i&&j1+1<=j)maxn=max(maxn,f[from][++j1]),++i1;
f[now][j]=max(f[now][j],maxn+b[i].se-b[i].fi+1);
while(!q.empty()&&f[from][q.back()]-b[q.back()+st-1].se<=f[from][j]-b[i-1].se)q.pop_back();
q.eb(j);
while(!q.empty()&&q.front()+st-1<pre[i])q.pop_front();
if(!q.empty())f[now][j]=max(f[now][j],f[from][q.front()]+b[i].se-b[q.front()+st-1].se);
if(j+n-i>=m)ans=max(ans,f[now][j]);
}
if(vis[st])last=pos[st];
for(int i=r;i>=pos[pre[st]];--i)Val[i]=-inf;
while(!Q.empty()&&h[Q.back()]-b[Q.back()].se<=h[st]-b[st].se)Q.pop_back();
Q.eb(st);
}
write(ans,'\n');
}
