[FJOI2007]轮状病毒

Description
轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的，2个原子之间的边表示这2个原子之间的信息通道。如下图所示

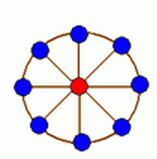
N轮状病毒的产生规律是在一个N轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有16个不同的3轮状病毒，如下图所示

现给定n(N<=100)，编程计算有多少个不同的n轮状病毒

Input
第一行有1个正整数n

Output
计算出的不同的n轮状病毒数输出

Sample Input
3

Sample Output
16

---

基尔霍夫矩阵？？貌似是的，但是我不会……
所以，打表出奇迹！
我们通过耗费大量的时间手动推出前8个轮状病毒的个数
1,5,16,45,121,320,841,2205,...
然后，找规律！
通过数学知识与大胆猜想，我们推出递推式为\(f[i]=3\times f[i-1]-f[i-2]+2\)
大胆交一发，WA掉……递推式错了？不，没开高精度……
加上高精度这题就可以愉快的A掉啦~

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int base=1e4;
const int digit=4;
const int maxn=15;
const int N=1e2;
struct Bignum{
	int v[maxn],len;
	Bignum(){memset(v,0,sizeof(v)),len=1;}
	void write(){
		printf("%d",v[len-1]);
		for (int i=len-2;~i;i--)	printf("%0*d",digit,v[i]);
		putchar('\n');
	}
}f[N+10];
Bignum operator +(const Bignum &x,const int &y){
	Bignum z;
	z.len=x.len; z.v[0]=y;
	for (int i=0;i<=z.len;i++)	z.v[i]+=x.v[i],z.v[i+1]+=z.v[i]/base,z.v[i]%=base;
	while (z.v[z.len])	z.v[z.len+1]=z.v[z.len]/base,z.v[z.len]%=base,z.len++;
	return z;
}
Bignum operator -(const Bignum &x,const Bignum &y){
	Bignum z;
	z.len=x.len;
	for (int i=0;i<=z.len;i++){
		z.v[i]+=x.v[i]-y.v[i];
		if (z.v[i]<0)	z.v[i+1]--,z.v[i]+=base;
	}
	while (!z.v[z.len-1]&&z.len>1)	z.len--;
	return z;
}
Bignum operator *(const Bignum &x,const int &y){
	Bignum z;
	z.len=x.len;
	for (int i=0;i<=z.len;i++)	z.v[i]+=x.v[i]*y,z.v[i+1]+=z.v[i]/base,z.v[i]%=base;
	while (z.v[z.len])	z.v[z.len+1]=z.v[z.len]/base,z.v[z.len]%=base,z.len++;
	return z;
}
int main(){
	int n=read();
	f[1].v[0]=1;
	for (int i=2;i<=n;i++)	f[i]=f[i-1]*3-f[i-2]+2;
	f[n].write();
	return 0;
}