[POI2007]旅游景点atr

Description
FGD想从成都去上海旅游。在旅途中他希望经过一些城市并在那里欣赏风景，品尝风味小吃或者做其他的有趣的事情。经过这些城市的顺序不是完全随意的，比如说FGD不希望在刚吃过一顿大餐之后立刻去下一个城市登山，而是希望去另外什么地方喝下午茶。幸运的是,FGD的旅程不是既定的，他可以在某些旅行方案之间进行选择。由于FGD非常讨厌乘车的颠簸，他希望在满足他的要求的情况下，旅行的距离尽量短，这样他就有足够的精力来欣赏风景或者是泡MM了^_.整个城市交通网络包含N个城市以及城市与城市之间的双向道路M条。城市自1至N依次编号，道路亦然。没有从某个城市直接到它自己的道路，两个城市之间最多只有一条道路直接相连，但可以有多条连接两个城市的路径。任意两条道路如果相遇，则相遇点也必然是这N个城市之一，在中途，由于修建了立交桥和下穿隧道，道路是不会相交的。每条道路都有一个固定长度。在中途，FGD想要经过K(K<=N-2)个城市。成都编号为1，上海编号为N,而FGD想要经过的N个城市编号依次为2,3,…,K+1.举例来说，假设交通网络如下图。FGD想要经过城市2,3,4,5，并且在2停留的时候在3之前，而在4,5停留的时候在3之后。那么最短的旅行方案是1-2-4-3-4-5-8,总长度为19。注意FGD为了从城市2到城市4可以路过城市3,但不在城市3停留。这样就不违反FGD的要求了。并且由于FGD想要走最短的路径，因此这个方案正是FGD需要的。

Input
第一行包含3个整数N(2<=N<=20000),M(1<=M<=200000),K(0<=K<=20),意义如上所述。
之后有q条限制，每次给一对\(x_i,y_i\)，代表\(x_i\)要在\(y_i\)之前休息过

Output
只包含一行，包含一个整数，表示最短的旅行距离。

Sample Input
8 15 4
1 2 3
1 3 4
1 4 4
1 6 2
1 7 3
2 3 6
2 4 2
2 5 2
3 4 3
3 6 3
3 8 6
4 5 2
4 8 6
5 7 4
5 8 6
3
2 3
3 4
3 5

Sample Output
19

HINT

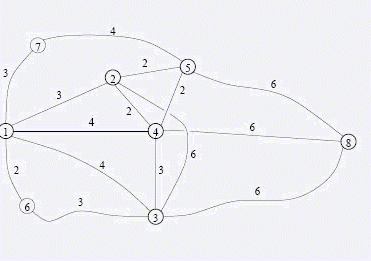
上图为题中所给出的例子

---

这题我不想说什么，题目输入描述都不讲清楚……看到k<=20，这不直接上状压吗
把1~k+1这些点之间的距离去全部处理出来，然后对于每个点记上一个限制，就可以愉快地用状压DP了
有K=0的情况，被坑了

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline void write(int x){
	if (x>=10)	write(x/10);
	putchar(x%10+'0');
}
const int N=2e4,M=2e5,K=20;
int pre[(M<<1)+10],now[N+10],child[(M<<1)+10],val[(M<<1)+10];
int h[N+10],deep[N+10];
bool vis[N+10];
int dis[K+5][K+5],f[21][1<<K],v[K+5];
int n,m,k,tot,Ans=inf;
void join(int x,int y,int z){pre[++tot]=now[x],now[x]=tot,child[tot]=y,val[tot]=z;}
void SPFA(int x){//预处理，dijkstra会快一些，但是我懒
	memset(vis,0,sizeof(vis));
	memset(deep,63,sizeof(deep));
	int head=0,tail=1;
	h[1]=x,vis[x]=1,deep[x]=0;
	while (head!=tail){
		if (++head>N)	head=1;
		int Now=h[head];
		for (int p=now[Now],son=child[p];p;p=pre[p],son=child[p]){
			if (deep[son]>deep[Now]+val[p]){
				deep[son]=deep[Now]+val[p];
				if (!vis[son]){
					if (++tail>N)	tail=1;
					vis[h[tail]=son]=1;
				}
			}
		}
		vis[Now]=0;
	}
	for (int i=1;i<=k+1;i++)	dis[x][i]=deep[i];
	dis[x][0]=deep[n];
}
void dp(){
	memset(f,63,sizeof(f));
	for (int i=1;i<=k;i++)	if (!v[i])	f[i][1<<(i-1)]=dis[1][i+1];
	for (int sta=1;sta<1<<k;sta++){
		for (int i=1;i<=k;i++){
			if ((f[i][sta]==inf)||(!(sta&(1<<(i-1)))))	continue;
			for (int j=1;j<=k;j++){
				if (((v[j]&sta)==v[j])&&(!(sta&(1<<(j-1))))){
					f[j][sta|(1<<(j-1))]=min(f[j][sta|(1<<(j-1))],f[i][sta]+dis[i+1][j+1]);
				}
			}
		}
	}
}
int main(){
	n=read(),m=read(),k=read();
	for (int i=1;i<=m;i++){
		int x=read(),y=read(),z=read();
		join(x,y,z),join(y,x,z);
	}
	if (!k){SPFA(1);printf("%d\n",deep[n]);return 0;}//特判
	for (int i=1;i<=k+1;i++)	SPFA(i);
	int q=read();
	for (int i=1;i<=q;i++){//由于他要经过的点是2~k+1，所以处理起来会有点小恶心
		int x=read(),y=read();
		v[y-1]|=1<<(x-2);
	}
	dp();
	for (int i=1;i<=k;i++)	Ans=min(Ans,f[i][(1<<k)-1]+dis[i+1][0]);
	printf("%d\n",Ans);
}