"蔚来杯"2022牛客暑期多校训练营4
A.Task Computing
给定\(n\)个任务,每个任务有两个权值\(w_i,p_i\),从中按任意顺序选出\(m\)个任务\((a_1,a_2,...,a_m)\),收益为\(\sum\limits_{i=1}^mw_{a_i}\prod\limits_{j=0}^{i-1}p_{a_j}\),求最大收益
考虑选出来的任务下标序列为\((a_1,a_2,...,a_m)\),考虑中间的两个下标\(x,y\),记\(x\)在\(y\)前面的收益\(R_x=\sum\limits_{i=1}^{x-1}w_{a_i}\prod\limits_{j=0}^{i-1}p_{a_j}+w_{a_x}\prod\limits_{j=0}^{x-1}p_{a_j}+w_{a_y}p_{a_x}\prod\limits_{j=0}^{x-1}p_{a_j}+\sum\limits_{y+1}^mw_{a_i}\prod\limits_{j=0}^{i-1}p_{a_j}\),记\(y\)在\(x\)前面的收益\(R_y=\sum\limits_{i=1}^{x-1}w_{a_i}\prod\limits_{j=0}^{i-1}p_{a_j}+w_{a_y}\prod\limits_{j=0}^{x-1}p_{a_j}+w_{a_x}p_{a_y}\prod\limits_{j=0}^{x-1}p_{a_j}+\sum\limits_{y+1}^mw_{a_i}\prod\limits_{j=0}^{i-1}p_{a_j}\),如果\(x\)在前面更优,则有\(R_x-R_y=(w_{a_x}+w_{a_y}p_{a_x}-w_{a_y}-w_{a_x}p_{a_y})\prod\limits_{j=0}^{x-1}p_{a_j}\geqslant 0\),将其转化可得到\(w_{a_x}(1-p_{a_y})\geqslant w_{a_y}(1-p_{a_x})\)
故我们对所有任务按照上述规则排序,最优解一定是这样排序后的子序列。我们设\(F[i][j]\)表示前\(i\)个任务里选了\(j\)个任务的最大价值,则转移即为\(F[i][j]=\max\{F[i+1][j],F[i+1][j-1]\times p_i+w_i\}\)(倒序枚举相当于每次新增的数放在序列最前面,方便更新答案)
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
const int N = 1e5, M = 20;
struct NODE {
double w, q, p;
NODE() { w = q = p = 0; }
void init() { p = 1.0 * q / 10000; }
bool operator<(const NODE& ots)const { return w * (1 - ots.p) < ots.w * (1 - p); }
}nodes[N + 10];
double F[N + 10][M + 10];
int main() {
int n = read(0), m = read(0);
for (int i = 1; i <= n; i++) nodes[i].w = read(0);
for (int i = 1; i <= n; i++) nodes[i].q = read(0);
for (int i = 1; i <= n; i++) nodes[i].init();
sort(nodes + 1, nodes + 1 + n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= min(i, m); j++)
F[i][j] = max(F[i - 1][j], F[i - 1][j - 1] * nodes[i].p + nodes[i].w);
printf("%.10lf\n", F[n][m]);
return 0;
}
B.2D Internet Angel
给定两个同心圆,内圆给出\(n\)个切点构成的凸多边形。现在在凸多边形与外圆之间随机均匀的选一个点,记这个点到\(n\)个切点之中的最小距离为\(X\),求\(E(X^2)\)
建立Vonoroi图,然后手动推二重积分式子,咕咕咕
C.Easy Counting Problem
统计长度为\(n\)且数位\(i\)出现至少\(c_i\)次的数字串数量
生成函数+NTT,咕咕咕
D.Jobs (Easy Version)
有\(n\)个公司,第\(i\)个公司有\(m_i\)个工作,每项工作对三项能力值(IQ,EQ,AQ)有要求。一个人只要能胜任公司的任意一项工作便可以去该公司任职
\(q\)次询问,每次询问给定一个三元组代表一个人的三项能力值,求这个人能去多少公司任职?
(强制在线,\(n\leqslant 10,\sum m_i\leqslant 10^6,q\leqslant 2\times 10^6,c\leqslant 400\),\(c\)为能力值上限)
由于\(n\)很小,所以我们考虑预处理。记\(F[i][x][y]\)表示需要在第\(i\)家公司任职,当前两项能力值为\(x,y\)时,第三项能力值所需的最小值
每次读入\(x,y,z\)时,可以令\(F[i][x][y]=\min\{F[i][x][y],z\}\),在读入完\(m_i\)个工作后,在进行一次前缀和扫描更新,有\(F[i][x][y]=\min\{F[i][x][y],F[i][x-1][y],F[i][x][y-1]\}\)
此后每次询问时,暴力枚举该人是否满足公司的条件即可,复杂度为\(O(n\sum m_i+c^3+nq)\)
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<random>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
const int N = 10, V = 4e2, P = 998244353;
int F[N + 10][V + 10][V + 10], seed;
void prepare(int pos) {
for (int i = 1; i <= V; i++)
for (int j = 1; j <= V; j++)
F[pos][i][j] = min(F[pos][i][j], min(F[pos][i - 1][j], F[pos][i][j - 1]));
}
int mlt(int a, int b) {
int res = 1;
for (; b; b >>= 1, a = 1ll * a * a % P)
if (b & 1) res = 1ll * res * a % P;
return res;
}
int solve(int x, int y, int z, int n) {
int Cnt = 0;
for (int i = 1; i <= n; i++)
Cnt += F[i][x][y] <= z;
return Cnt;
}
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n = read(0), q = read(0);
memset(F, 0x7f, sizeof(F));
for (int i = 1; i <= n; i++) {
int m = read(0);
for (int j = 1; j <= m; j++) {
int x = read(0), y = read(0), z = read(0);
F[i][x][y] = min(F[i][x][y], z);
}
prepare(i);
}
seed = read(0);
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1, 400);
int LastAns = 0, Ans = 0;
for (int i = 1; i <= q; i++) {
int IQ = (u(rng) ^ LastAns) % 400 + 1;
int EQ = (u(rng) ^ LastAns) % 400 + 1;
int AQ = (u(rng) ^ LastAns) % 400 + 1;
LastAns = solve(IQ, EQ, AQ, n);
Ans = (Ans + 1ll * LastAns * mlt(seed, q - i)) % P;
}
printf("%d\n", Ans);
return 0;
}
E.Jobs (Hard Version)
与上一题题面完全相同,唯一不同的点在于\(n\leqslant 10\Longrightarrow n\leqslant 10^6\)
考虑容斥,首先我们对问题的简化版本,即二维进行分析。
考虑按照第一能力值升序排序,显然,如果一个工作的两个能力值都比另一个工作大,那么它对答案而言是没有贡献的,去掉这样的工作后,剩下的工作一定呈下降阶梯状,即\(x\)递增,\(y\)递减
这样的话,每份工作左上角对应的对角矩阵区域(即\(x'>x\And y'>y\))的区域的并即为可在该公司工作的能力值区域,求出这段区域我们差分即可(在绿点+1,在红点-1)
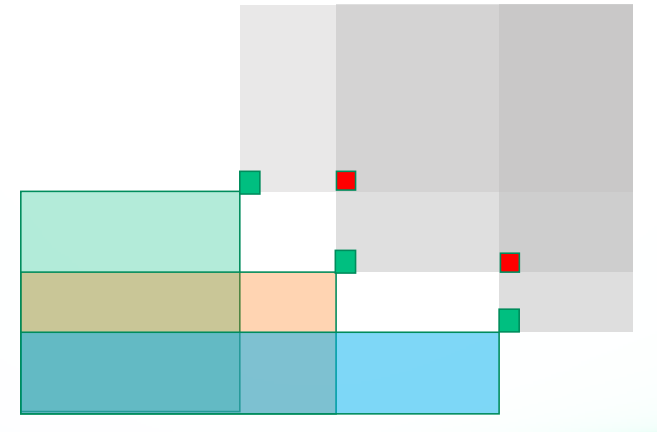
考虑三维,我们可以枚举第三维的值,将其划分为\(\min(m,c)\)个二维差分的形式,每一层都是一个二维问题。对于第三维度的每一层,只有一个工作的第三个维度小于等于该层数值时,才能在这一层做贡献,复杂度为\(O(\min(m,c)\sum m_i+c^3+q)\)
上述的做法需要较为精细的实现才能通过,因此我们继续优化。考虑到按照第三维度排序后,每份工作对应的二维矩阵只会加入删除一次,因此可以即时更新加入和删除一个工作的影响,用set维护即可。这样复杂度降到了\(O(\log m\sum m_i+c^3+q)\),可以通过
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<random>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
struct node {
int x, y;
node(int _x, int _y) { x = _x, y = _y; }
bool operator<(const node& ots)const { return x != ots.x ? x < ots.x : y < ots.y; }
};
const int V = 4e2, M = 1e6, P = 998244353;
int a[M + 10], b[M + 10], c[M + 10], pos[M + 10];
int Map[V + 10][V + 10][V + 10];
int main() {
int n = read(0), q = read(0);
for (int i = 1; i <= n; i++) {
int m = read(0);
for (int j = 1; j <= m; j++)
a[j] = read(0), b[j] = read(0), c[j] = read(0), pos[j] = j;
sort(pos + 1, pos + 1 + m, [](int x, int y) { return c[x] < c[y]; });
set<node>temp;
for (int j = 1; j <= m; j++) {
while (true) {
auto it = temp.lower_bound(node(a[pos[j]], 0));
if (it == temp.end()) break;
if (it->y >= b[pos[j]]) {
Map[it->x][it->y][c[pos[j]]]--;
int nx = it->x, ny = it->y, tx = 0, ty = 0;
if (it != temp.begin()) {
it--;
Map[nx][ty = it->y][c[pos[j]]]++;
it++;
}
it++;
if (it != temp.end())
Map[tx = it->x][ny][c[pos[j]]]++;
it--;
temp.erase(it);
if (tx && ty)
Map[tx][ty][c[pos[j]]]--;
}
else break;
}
auto it = temp.lower_bound(node(a[pos[j]], iMax));
int tx = 0, ty = 0;
if (it != temp.begin()) {
it--;
if (it->y <= b[pos[j]]) continue;
Map[a[pos[j]]][ty = it->y][c[pos[j]]]--;
it++;
}
if (it != temp.end())
Map[tx = it->x][b[pos[j]]][c[pos[j]]]--;
if (tx && ty)
Map[tx][ty][c[pos[j]]]++;
Map[a[pos[j]]][b[pos[j]]][c[pos[j]]]++;
temp.insert(node(a[pos[j]], b[pos[j]]));
}
}
for (int i = 1; i <= V; i++)
for (int j = 1; j <= V; j++)
for (int k = 1; k <= V; k++)
Map[i][j][k] += Map[i][j][k - 1];
for (int i = 1; i <= V; i++)
for (int j = 1; j <= V; j++)
for (int k = 1; k <= V; k++)
Map[i][j][k] += Map[i][j - 1][k];
for (int i = 1; i <= V; i++)
for (int j = 1; j <= V; j++)
for (int k = 1; k <= V; k++)
Map[i][j][k] += Map[i - 1][j][k];
int seed = read(0);
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1, 400);
int LastAns = 0, Ans = 0;
for (int i = 1; i <= q; i++) {
int IQ = (u(rng) ^ LastAns) % 400 + 1;
int EQ = (u(rng) ^ LastAns) % 400 + 1;
int AQ = (u(rng) ^ LastAns) % 400 + 1;
LastAns = Map[IQ][EQ][AQ];
Ans = (1ll * Ans * seed + LastAns) % P;
}
printf("%d\n", Ans);
return 0;
}
F.Palindromic Tree
给定一棵树,点上有字符'0'和'1',多次询问,求一条简单路径形成的串的本质不同回文子串数
树上回滚莫队+支持双端插入和撤回的回文自动机
G.Wall Builder I
给定一个大矩形,矩形边上有\(n\)个点,每次可以选取一个未选取的点,向矩形内部引一条垂直点所在边的垂线,垂线碰到其他垂线或边框时停止。自定义一个引垂线的顺序,使得最后矩形被分割成的最大小矩中最大
各种分类讨论,咕咕咕
H.Wall Builder II
有\(n\)个\(1\times 1\)的矩形,\(n-1\)个\(2\times 1\)的矩形,...,1个\(n\times 1\)的矩形,将它们拼成一个大矩形,问最小周长
总面积\(S=\frac{n(n+1)(n+2)}{6}\),枚举其边长\(a\times b=S\),再将所有板子从大到小按行依次贪心填即可
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
bool Check(int n, int x, int y) {
vector<int>Len(x, 0);
for (int i = n; i; i--) {
int Cnt = n - i + 1;
while (Cnt--) {
for (int j = 0; j < x; j++) {
if (Len[j] + i <= y) {
Len[j] += i;
goto End;
}
}
return false;
End:;
}
}
return true;
}
void solve(int n, int x, int y) {
vector<int>Len(x, 0);
for (int i = n; i; i--) {
int Cnt = n - i + 1;
while (Cnt--) {
for (int j = 0; j < x; j++) {
if (Len[j] + i <= y) {
printf("%d %d %d %d\n", Len[j], j, Len[j] + i, j + 1);
Len[j] += i;
break;
}
}
}
}
}
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int T = read(0);
while (T--) {
int n = read(0), S = n * (n + 1) * (n + 2) / 6, Ans = iMax;
for (int i = 1; i <= (int)sqrt(S); i++) {
if (S % i) continue;
if (Check(n, i, S / i))
Ans = min(Ans, (i + S / i) << 1);
}
printf("%d\n", Ans);
for (int i = 1; i <= (int)sqrt(S); i++) {
if (S % i) continue;
if ((i + S / i) << 1 == Ans)
solve(n, i, S / i);
}
}
return 0;
}
I.Three Body
给定一大一小两个\(k\)维数组\(S,T\),定义一个位置匹配为将\(T\)放在此处后,所有\(S\)中的元素大于等于\(T\)中的元素,元素范围为\(1\sim K\),问有多少个匹配位置
构造+FFT
J.Counting Fish Again
给定无穷大的网格图,左下角为\((0,0)\),有\(m\)次操作,每次添加或删除一条斜率为-1的线段,输出图中“鱼”的数量
“鱼”定义为一个正方形加上一个等边直角三角形,且正方形边长与三角形直角边长相等,三角形与正方形恰有一个顶点重合
set维护斜线+分类讨论
K.NIO's Sword
初始给定攻击力为0的剑,需要依次击杀\(n\)个敌人,当且仅当攻击力\(x\equiv i\%n\)时才可击杀第\(i\)个敌人。玩家可以随时升级剑,每次升级可以让剑攻击力变为\(10x+c\)(\(c\)为任意\(<10\)的自然数),问最少升级多少次才能打败所有敌人?
考虑到击杀第\(i-1\)个敌人后,当前攻击力在膜\(n\)意义下必然为\(i-1\),则击杀第\(i\)个敌人的攻击力满足\((i-1)\times 10^k+c_k\equiv i\%n\),其中\(c_k\in[0,10^k)\),对于一个固定的\(k\)而言,攻击力的下界与上界是可以被确定的,我们只需要让\(k\)慢慢增大,考虑其攻击力上下界是否包含\(i\)即可
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n = read(0);
if (n == 1) {
printf("0\n");
return 0;
}
int Now = 0, Ans = 0;
for (int i = 1; i < n; i++) {
int Len = 0;
while (true) {
Now = 10ll * Now % n;
Len = Len * 10 + 9;
Ans++;
if (Now <= i) {
if (Now + Len >= i)
break;
}
else {
if (Len >= n)
break;
if (Now + Len > n && (Now + Len) % n >= i)
break;
}
}
Now = i;
}
int Len = 0;
while (true) {
Now = 10ll * Now % n;
Len = Len * 10 + 9;
Ans++;
if (Now <= 0) {
if (Now + Len >= 0)
break;
}
else {
if (Len >= n)
break;
if (Now + Len > n && (Now + Len) % n >= 0)
break;
}
}
printf("%d\n", Ans);
return 0;
}
L.Black Hole
求变长为\(a\)的凸正\(n\)面体收缩\(k\)次后的面数和边长,一次收缩定义为该几何体所有面中心的三维凸包
考虑欧拉公式:\(V+F-E=2\),取凸多面体的一个顶点,设其向外有\(n\)条棱;再取其一个面,设其为正\(m\)边形,由于顶点附近的角之和需要小于360°,则有:\(n(180-\frac{360}{m})<360\Rightarrow 1-\frac{2}{m}<\frac{2}{n}\),可得其有五个解集:\((m,n)\in\{(3,3),(3,4),(3,5),(4,3),(5,3)\}\),若用\(V,F\)来表示\(E\),则有\(E=\frac{nV}{2}=\frac{mF}{2}\),代入解得\(F= 4,6,8,12,20\),即可行的凸正面体仅有五种情况
(其实在Wikipedia上搜索Platonic solid就行)
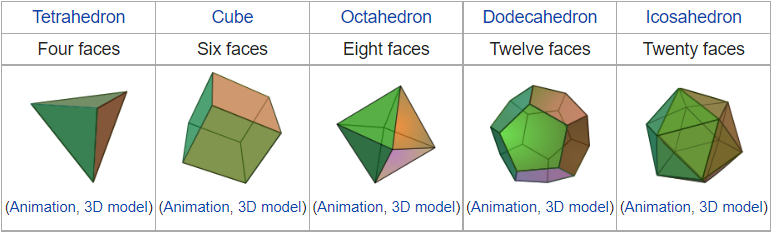
再手玩一下可以发现正四面体转化为正四面体,正六面体和正八面体互相转化,正十二面体和正二十面体互相转化
再动用一下立体几何思想,可以得到:

/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
void solve(int& n, double& a) {
switch (n) {
case 4:
a = a / 3;
break;
case 6:
a = a / sqrt(2), n = 8;
break;
case 8:
a = sqrt(2) * a / 3, n = 6;
break;
case 12:
a = (3 * sqrt(5) + 5) * a / 10, n = 20;
break;
case 20:
a = (sqrt(5) + 1) * a / 6, n = 12;
break;
default:break;
}
}
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int T = read(0);
while (T--) {
int n = read(0), a = read(0), k = read(0);
if (n != 4 && n != 6 && n != 8 && n != 12 && n != 20) {
printf("impossible\n");
continue;
}
double _a = a;
while (k--) solve(n, _a);
printf("possible %d %.10lf\n", n, _a);
}
return 0;
}
M.Monotone Chain
给定平面上\(n\)个点\(A_1,A_2,...,A_n\),求一组\(a,b\in \R^2\),使得对于任意\(1\leqslant i\leqslant j\leqslant n\),都有\((OA_i-a)\cdot b\leqslant (OA_j-a)\cdot b\)
我们将条件转化一下,可得满足\(OA_i\cdot b\leqslant OA_j\cdot b\)即可。故题目转化为,找到一条有向直线,使得\(A_1,A_2,...,A_n\)在直线上的投影是单调的。
对于每条有向线段进行考虑,直线的方向只可能在该线段方向的顺逆90°构成的半平面内,我们对每个线段进行考虑,即可求出直线方向的可行区间
如何求?记\(L,R\)两个边界方向,再用叉积判断即可
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
struct Point {
int x, y;
Point(int _x = 0, int _y = 0) :x(_x), y(_y) {}
void Read() { x = read(0), y = read(0); }
Point& operator =(const Point& ots) {
x = ots.x, y = ots.y;
return *this;
}
void print() {
printf("%d %d\n", x, y);
}
};
Point operator -(const Point& A, const Point& B) { return Point(A.x - B.x, A.y - B.y); }
Point operator +(const Point& A, const Point& B) { return Point(A.x + B.x, A.y + B.y); }
ll operator *(const Point& A, const Point& B) { return 1ll * A.x * B.y - 1ll * B.x * A.y; }
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n = read(0);
Point Last, Now, vec; Last.Read();
Point L(0, 1), R; bool Flag = 0;
for (int i = 1; i < n; i++) {
Now.Read();
vec = Now - Last;
Last = Now;
if (!vec.x && !vec.y) continue;
Point l(-vec.y, vec.x), r(vec.y, -vec.x);
if (!Flag) {
L = l, R = r;
Flag |= true;
continue;
}
if ((l * R > 0) && (r * L) < 0) {
printf("NO\n");
return 0;
}
if (l * L > 0) L = l;
if (r * R < 0) R = r;
}
printf("YES\n0 0 %d %d\n", L.x, L.y);
return 0;
}
N.Particle Arts
给定\(n\)个粒子,每个粒子有能量\(a_i\),两个粒子相撞会使得两个粒子能量变成\(a\And b,a\vert b\),问最终粒子能量稳定后的方差
考虑什么时候粒子能量稳定,不难发现此时必有\(a\And b=a\)或者\(a\And b=b\),即任意两个粒子之间的能量关系在二进制下都是包含关系。将此时的\(a_i\)降序排序,对于二进制的每一位而言,必然为前一段连续的1,后一段连续的0,故我们贪心的填即可得到最终的\(a_i\)
至于算方差……
- \(\mu=\frac{1}{n}\sum\limits_{i=1}^na_i,\sigma^2=\frac{1}{n}\sum\limits_{i=1}^n(a_i-\mu)^2=\frac{1}{n^3}\sum\limits_{i=1}^n(na_i-\sum\limits_{j=1}^na_j)^2\),这样会炸longlong,得开int128
- \(D(x)=E(X^2)-E^2(X)=\frac{1}{n}\sum\limits_{i=1}^na_i^2-\frac{1}{n^2}(\sum\limits_{i=1}^na_i)^2=\frac{\sum\limits_{i=1}^na_i^2-(\sum\limits_{j=1}^na_j)^2}{n^2}\),这样就不会炸longlong了
/*program from Wolfycz*/
#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lMax 1e18
#define MK make_pair
#define iMax 0x7f7f7f7f
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define UNUSED(x) (void)(x)
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
template<typename T>inline T read(T x) {
int f = 1; char ch = getchar();
for (; ch < '0' || ch>'9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void print(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
}
const int M = 15;
int Cnt[M + 10];
ll gcd(ll x, ll y) { return !y ? x : gcd(y, x % y); }
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n = read(0);
for (int i = 1; i <= n; i++) {
int x = read(0);
for (int j = 0; j < M; j++)
if (x >> j & 1)
Cnt[j]++;
}
ll sum = 0, sum2 = 0;
for (int i = 1; i <= n; i++) {
int x = 0;
for (int j = 0; j < M; j++)
if (Cnt[j]-- > 0)
x |= 1 << j;
sum += x, sum2 += sqr(x);
}
ll a = n * sum2 - sqr(sum), b = 1ll * n * n;
ll c = gcd(a, b);
a /= c, b /= c;
printf("%lld/%lld\n", a, b);
return 0;
}


