[HDU2281]Square Number

Description
Find the biggest integer \(n (1\leqslant n\leqslant N)\) and an integer \(x\) to make them satisfy

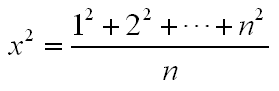
Input
The input consists of several test cases. Each test case contains a integer \(N, 1\leqslant N\leqslant 10^{18}\).The input ends with \(N = 0\).

Output
In one line for each case, output two integers \(n\) and \(x\) you have found.

Sample Input

1
2
0

Sample Output

1 1
1 1

---

根据自然数幂和可得 \(\sum\limits_{i=1}^ni^2=\frac{n(n+1)(2n+1)}{6}\)，将其代入原式可得 \(x^2=\frac{(n+1)(2n+1)}{6}\)

移项配方可得\((4n+3)^2-48x^2=1\)，满足Pell方程的形式，故可直接套用

关于Pell方程的详细推导及证明，由于本人未能看懂，故不在此赘述，兴趣可以参考以下几个链接

https://blog.csdn.net/u011815404/article/details/88717125

https://blog.csdn.net/ddaarsel63181/article/details/102408570

https://baike.baidu.com/item/佩尔方程/11029962?fr=aladdin#2_3

/*program from Wolfycz*/
#include<map>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define ll_inf 1e18
#define MK make_pair
#define pll pair<ll,ll>
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define int_inf 0x7f7f7f7f
#define pdd pair<double,double>
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
	static char buf[1000000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
	int f=1; char ch=gc();
	for (;ch<'0'||ch>'9';ch=gc())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=gc())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
template<typename T>inline T read(T x){
	int f=1; char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x<0)	putchar('-'),x=-x;
	if (x>9)	print(x/10);
	putchar(x%10+'0');
}
const int D=48;
vector<pll>vec,Ans;
void prepare(){
	vec.push_back(MK(7ll,1ll));
	Ans.push_back(MK(1ll,1ll));
	while (true){
		ll x=vec.back().Fi,y=vec.back().Se;
		ll _x=7*x+D*y,_y=x+7*y;
		if (_x<0)	break;
		vec.push_back(MK(_x,_y));
		if ((_x-3)%4)	continue;
		Ans.push_back(MK((_x-3)/4,_y));
	}
	Ans.push_back(MK((ll)1e18+5,0));
}
int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	prepare(); ll n;
	while (scanf("%lld",&n)!=EOF&&n){
		for (int i=0;i<(int)Ans.size();i++){
			if (Ans[i].Fi>n){
				printf("%lld %lld\n",Ans[i-1].Fi,Ans[i-1].Se);
				break;
			}
		}
	}
	return 0;
}