[HDU1724]Ellipse

Description
Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..
Look this sample picture:

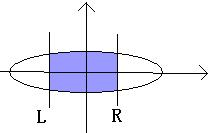
A ellipses in the plane and center in point O. the L,R lines will be vertical through the X-axis. The problem is calculating the blue intersection area. But calculating the intersection area is dull, so I have turn to you, a talent of programmer. Your task is tell me the result of calculations.(defined PI=3.14159265 , The area of an ellipse A=PI*a*b )

Input
Input may contain multiple test cases. The first line is a positive integer N, denoting the number of test cases below. One case One line. The line will consist of a pair of integers a and b, denoting the ellipse equation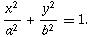, A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).

Output
For each case, output one line containing a float, the area of the intersection, accurate to three decimals after the decimal point.

Sample Input

2
2 1 -2 2
2 1 0 2

Sample Output

6.283
3.142

---

虽然说是Simpson积分……不过直接用普通的积分也是可行的

由于椭圆上下对称，故我们对上半部分积分即可

将 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) 化简得 \(y=b\sqrt{1-\frac{x^2}{a^2}}\) ，将\(a\)提出来得 \(y=\frac{b}{a}\sqrt{a^2-x^2}\)

我们考虑求 \(\int\sqrt{a^2-x^2}\ dx\)，令 \(x=a\sin t\)，则 \(dx=a\cos t\ dt\)

故原式化为 \(\int\sqrt{a^2-a^2\sin^2t}\ a\cos t\ dt=\int a^2\cos^2t\ dt=\frac{a^2}{4}\int (\cos 2t+1)\ d(2t)=\frac{a^2}{4}(\sin 2t+2t)+C\)

再化简得 \(\frac{a\sin t}{2}a\cos t+\frac{a^2t}{2}+C\)

将 \(x=a\sin t\) 代入得 \(\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin(\frac{x}{a})+C\)

最后原式需要计算\(S=\int_l^ry(x)\ dx\)，我们将\(y(x)=\frac{b}{a}\sqrt{a^2-x^2}\)代入，再根据上述推导过程推导即可

也可以利用椭圆的左右对称，直接从0积分到\(l\)或\(r\)，然后根据其位置加减即可

/*program from Wolfycz*/
#include<map>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define ll_inf 1e18
#define MK make_pair
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define int_inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
	static char buf[1000000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
	int f=1; char ch=gc();
	for (;ch<'0'||ch>'9';ch=gc())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=gc())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
template<typename T>inline T read(T x){
	int f=1; char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x<0)	putchar('-'),x=-x;
	if (x>9)	print(x/10);
	putchar(x%10+'0');
}
double F(int a,int x){return x/2.0*sqrt(sqr(a)-sqr(x))+sqr(a)/2.0*asin(1.0*x/a);}
int main(){
	int T=read(0);
	while (T--){
		int a=read(0),b=read(0),l=read(0),r=read(0);
		double resl=F(a,abs(l)),resr=F(a,abs(r)),Ans=0;
//		printf("%lf %lf\n",resl,resr);
		if (l*r>0)	Ans=abs(resl-resr);
		else	Ans=resl+resr;
		printf("%.3lf\n",2.0*b/a*Ans);
	}
	return 0;
}