浅谈算法——AC自动机
在学习AC自动机之前,你需要两个前置知识:Trie树,KMP
首先我们需要明白,AC自动机是干什么的(用来自动AC的)
大家都知道KMP算法是求单字符串对单字符串的匹配问题的,那么多字符在单字符上匹配该怎么办?
我们举个栗子
——求 aabb 在 aabababbbabbabbababb 中出现了多少次?这个很明显KMP即可
——求 ab aab abbb abab bab 分别在 abbabbabababababba 中出现了多少次?嗯……对每个串分别跑一次KMP?这样如果串非常多的话,复杂度可想而知
那这个时候我们应该怎么办呢?当然是用AC自动机了
所以AC自动机是啥啊?
AC自动机:Aho-Corasick automation,该算法在1975年产生于贝尔实验室,是著名的多模匹配算法。——某度百科
算了,这东西看不看都一样,我们来正式讲解一下AC自动机
AC自动机需要预先知道所有西药匹配的串,例如:her she shr
然后我们对它们构建一棵Trie树
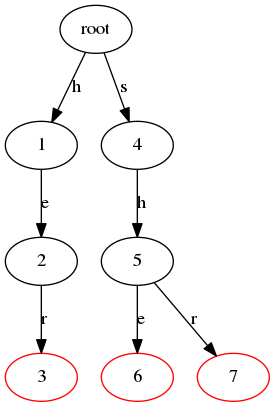
红色的是结束节点,然后我们在这棵Trie树上构建Fail指针,所谓Fail指针,就和KMP中的Next数组类似,我们先把构建好Fail指针的图放上来
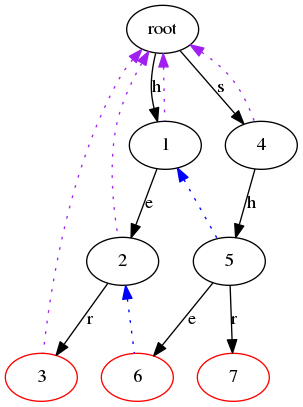
这图画的真TM丑……Graphviz这东西我还不太会用……
然后虚线箭头就是Fail指针(说是指针,拿数组存着也行),至于那些奇奇怪怪的颜色……不要在意这些细节
我们先不管Fail指针怎么建出来的,我们先看看这玩意干啥,每次沿着Trie树匹配,如果失配后,直接跳转到失配指针,然后继续匹配
比如现在在节点6,若要继续匹配'r',则沿着Fail指针跳跃,到节点2,然后既可以匹配'r'到3号节点
所以说,Fail指针其实就是KMP的Next数组,它的意义就是找到一个最长的等于其后缀的串
话说回来,Fail指针应该如何构建?从dalao的博客里得知:Fail指针是沿着其父亲的Fail指针,一路向上,直到找到拥有当前这个字母的子节点的节点的那个子节点
哇……感觉好复杂,我也是这么想的。不过,画个图一看,好像还真是这样,值得一提的是,第二层的所有节点的Fail指针都需要指向Trie树的根节点
建Fail指针算一个BFS的过程,因为每次要用到父亲节点的Fail指针,然后每次建Fail指针的时候都需要不断跳跳跳?当然不用,那我们该怎么办?
扔段代码看一下吧
void make_fail(){
static int h[N+10];
int head=1,tail=0;
for (int i=0;i<26;i++) if (trie[root][i]) h[++tail]=trie[root][i];
//预处理第二层的Fail指针
for (;head<=tail;head++){
int Now=h[head];
for (int i=0;i<26;i++){
if (trie[Now][i]){
int son=trie[Now][i];
fail[son]=trie[fail[Now]][i];
//子节点的Fail指针指向当前节点的Fail指针指向的节点的相同子节点
h[++tail]=son;
}else trie[Now][i]=trie[fail[Now]][i];
//不存在这个子节点的话,则将该节点实体化,方便之后的寻找(也就是不用跳跳跳了)
}
}
}
这个实际意义上来讲已经不是Trie树了,这应该是个Trie图,但如果碰到字符集大小非常巨大的时候,显然不能建Trie图,所以我们还是要暴力跳跳跳,然后也放段代码
void make_fail(){
static int h[N+10];
int head=1,tail=1; h[1]=root;
for (;head<=tail;head++){
int Now=h[head];
for (map<node,int>::iterator it=trie[Now].begin();it!=trie[Now].end();it++){
int p=fail[Now];
while (p&&trie[p].find(it->Fi)==trie[p].end()) p=fail[p];
//暴力跳跳跳
fail[it->Se]=p?trie[p].find(it->Fi)->Se:root;
h[++tail]=it->Se;
}
}
}
然后由于字符集很大,所以我们就用map来存储,然后我的map写法可能比较清奇,凑合着看吧……
然后Fail指针建完了,我们就可以直接匹配了~
贴个板子题好了
/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
static char buf[1000000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int frd(){
int x=0,f=1;char ch=gc();
for (;ch<'0'||ch>'9';ch=gc()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+'0');
}
const int N=1e6,M=1.5e4;
char str[200][100];
struct S1{
int trie[M+10][26],fail[M+10],End[M+10];
int root,tot;
void init(){
root=tot=0;
memset(End,0,sizeof(End));
memset(trie,0,sizeof(trie));
memset(fail,0,sizeof(fail));
}
void insert(int ID){
int len=strlen(str[ID]),p=root;
for (int i=0;i<len;i++){
if (!trie[p][str[ID][i]-'a']) trie[p][str[ID][i]-'a']=++tot;
p=trie[p][str[ID][i]-'a'];
}
End[p]=ID;
}
void make_fail(){
static int h[M+10];
int head=1,tail=0;
for (int i=0;i<26;i++) if (trie[root][i]) h[++tail]=trie[root][i];
for (;head<=tail;head++){
int Now=h[head];
for (int i=0;i<26;i++){
if (trie[Now][i]){
int son=trie[Now][i];
fail[son]=trie[fail[Now]][i];
h[++tail]=son;
}else trie[Now][i]=trie[fail[Now]][i];
}
}
}
void check(char *s,int n){
static int Ans[200];
memset(Ans,0,sizeof(Ans));
int len=strlen(s),p=root,Max=0;
for (int i=0;i<len;i++){
p=trie[p][s[i]-'a'];
for (int x=p;x;x=fail[x]) Ans[End[x]]++;
}
for (int i=1;i<=n;i++) Max=max(Max,Ans[i]);
printf("%d\n",Max);
for (int i=1;i<=n;i++) if (Max==Ans[i]) printf("%s\n",str[i]);
}
}AC;//Aho-Corasick automaton
char T[N+10];
int main(){
while (true){
AC.init();
int n=read();
if (!n) break;
for (int i=1;i<=n;i++){
scanf("%s",str[i]);
AC.insert(i);
}
AC.make_fail();
scanf("%s",T);
AC.check(T,n);
}
return 0;
}


