Java二叉树

树：二叉树

本文引用青空の霞光大佬的笔记

树是一种全新的数据结构，它就像一棵树的树枝一样，不断延伸。

树枝666

在我们的程序中，想要表示出一棵树，就可以像下面这样连接：

image-20220801210920230

可以看到，现在一个结点下面可能会连接多个节点，并不断延伸，就像树枝一样，每个结点都有可能是一个分支点，延伸出多个分支，从位于最上方的结点开始不断向下，而这种数据结构，我们就称为树（Tree）注意分支只能向后单独延伸，之后就分道扬镳了，不能与其他分支上的结点相交！

  • 我们一般称位于最上方的结点为树的根结点（Root）因为整棵树正是从这里开始延伸出去的。
  • 每个结点连接的子结点数目（分支的数目），我们称为结点的度（Degree），而各个结点度的最大值称为树的度。
  • 每个结点延伸下去的下一个结点都可以称为一棵子树（SubTree）比如结点B及其之后延伸的所有分支合在一起，就是一棵A的子树。
  • 每个结点的层次（Level）按照从上往下的顺序，树的根结点为1，每向下一层+1，比如G的层次就是3，整棵树中所有结点的最大层次，就是这颗树的深度（Depth），比如上面这棵树的深度为4，因为最大层次就是4。

由于整棵树错综复杂，所以说我们需要先规定一下结点之间的称呼，就像族谱那样：

  • 与当前结点直接向下相连的结点，我们称为子结点（Child），比如B、C、D结点，都是A的子结点，就像族谱中的父子关系一样，下一代一定是子女，相反的，那么A就是B、C、D的父结点（Parent），也可以叫双亲结点。
  • 如果某个节点没有任何的子结点（结点度为0时）那么我们称这个结点为叶子结点（因为已经到头了，后面没有分支了，这时就该树枝上长叶子了那样）比如K、L、F、G、M、I、J结点，都是叶子结点。
  • 如果两个结点的父结点是同一个，那么称这两个节点为兄弟结点（Sibling）比如B和C就是兄弟结点，因为都是A的孩子。
  • 从根结点开始一直到某个结点的整条路径的所有结点，都是这个结点的祖先结点（Ancestor）比如L的祖先结点就是A、B、E

那么在了解了树的相关称呼之后，相信各位就应该对树有了一定的了解，虽然概念比较多，但是还请各位一定记住，不然后面就容易听懵。

而我们本章需要着重讨论的是二叉树（Binary Tree）它是一种特殊的树，它的度最大只能为2，所以我们称其为二叉树，一棵二叉树大概长这样：

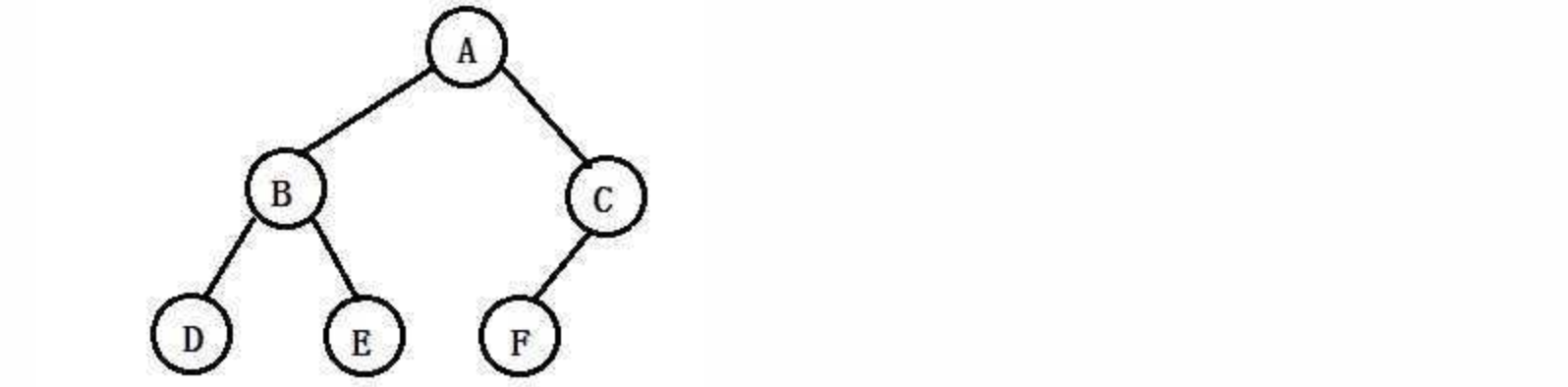
image-20220801224008266

并且二叉树任何结点的子树是有左右之分的，不能颠倒顺序，比如A结点左边的子树，称为左子树，右边的子树称为右子树。

当然，对于某些二叉树我们有特别的称呼，比如，在一棵二叉树中，所有分支结点都存在左子树和右子树，且叶子结点都在同一层：

image-20220801231216578

这样的二叉树我们称为满二叉树，可以看到整棵树都是很饱满的，没有出现任何度为1的结点，当然，还有一种特殊情况：

image-20220801224008266

可以看到只有最后一层有空缺，并且所有的叶子结点是按照从左往右的顺序排列的，这样的二叉树我们一般称其为完全二叉树，所以，一棵满二叉树，一定是一棵完全二叉树。

我们接着来看看二叉树在程序中的表示形式，我们在前面使用链表的时候，每个结点不仅存放对应的数据，而且会存放一个指向下一个结点的引用：

image-20220723171648380

而二叉树也可以使用这样的链式存储形式，只不过现在一个结点需要存放一个指向左子树的引用和一个指向右子树的引用了：

image-20220806111610082

通过这种方式，我们就可以通过连接不同的结点形成一颗二叉树了，这样也更便于我们去理解它，我们首先定义一个类：

public class TreeNode<E> {
    public E element;
    public TreeNode<E> left, right;

    public TreeNode(E element){
        this.element = element;
    }
}

比如我们现在想要构建一颗像这样的二叉树：

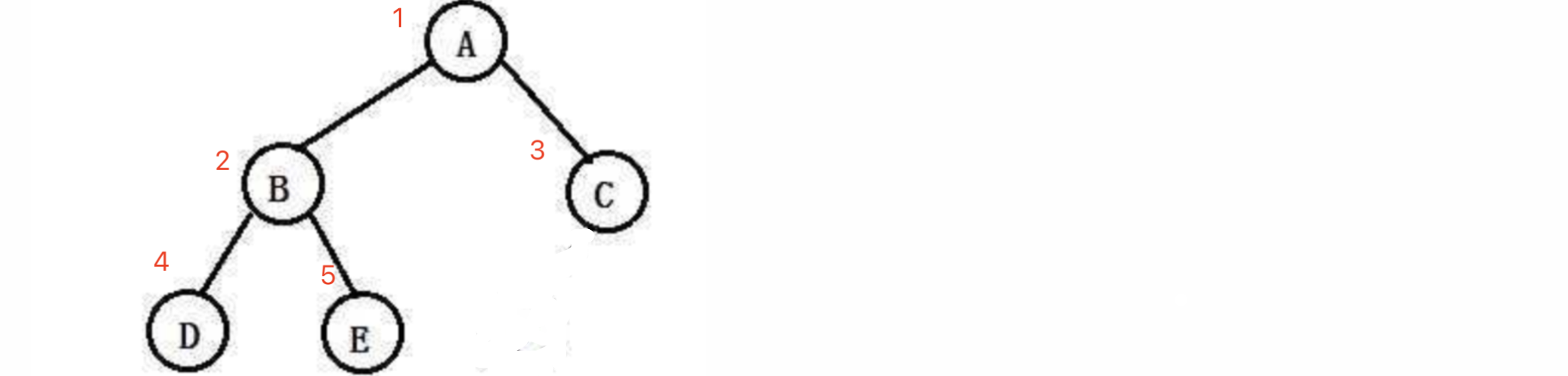
image-20220805231744693

首先我们需要创建好这几个结点：

public static void main(String[] args) {
    TreeNode<Character> a = new TreeNode<>('A');
    TreeNode<Character> b = new TreeNode<>('B');
    TreeNode<Character> c = new TreeNode<>('C');
    TreeNode<Character> d = new TreeNode<>('D');
    TreeNode<Character> e = new TreeNode<>('E');
    
}

接着我们从最上面开始，挨着进行连接，首先是A这个结点：

public static void main(String[] args) {
    ...
    a.left = b;
    a.right = c;
    b.left = d;
    b.right = e;
}

这样的话，我们就成功构建好了这棵二叉树，比如现在我们想通过根结点访问到D：

System.out.println(a.left.left.element);

断点调试也可以看的很清楚：

image-20220930160452608

这样，我们就通过使用链式结构，成功构建出了一棵二叉树，接着我们来看看如何遍历一棵二叉树，也就是说我们想要访问二叉树的每一个结点，由于树形结构特殊，遍历顺序并不唯一，所以一共有四种访问方式：前序遍历、中序遍历、后序遍历、层序遍历。不同的访问方式输出都结点顺序也不同。

首先我们来看最简单的前序遍历：

image-20220806171459056

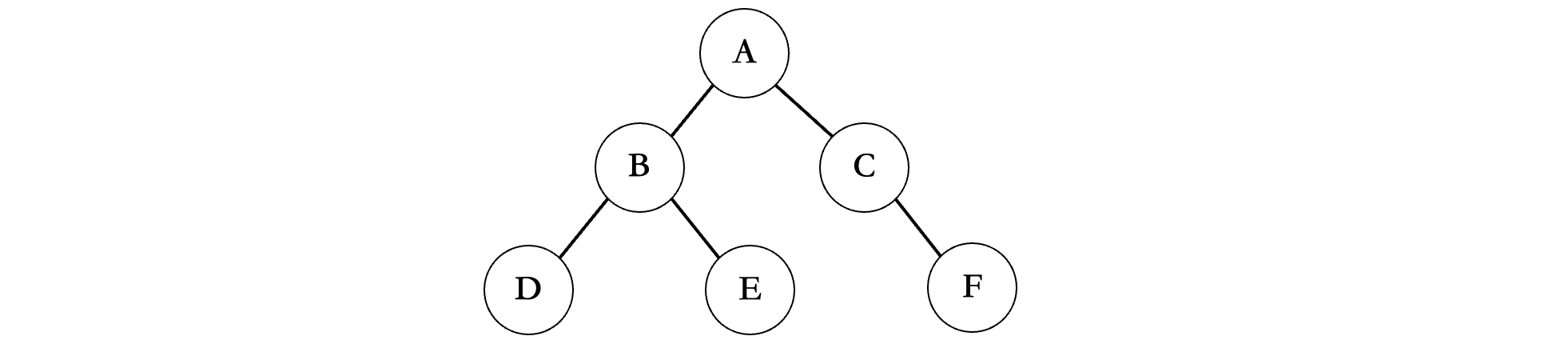
前序遍历是一种勇往直前的态度，走到哪就遍历到那里，先走左边再走右边，比如上面的这个图，首先会从根节点开始：

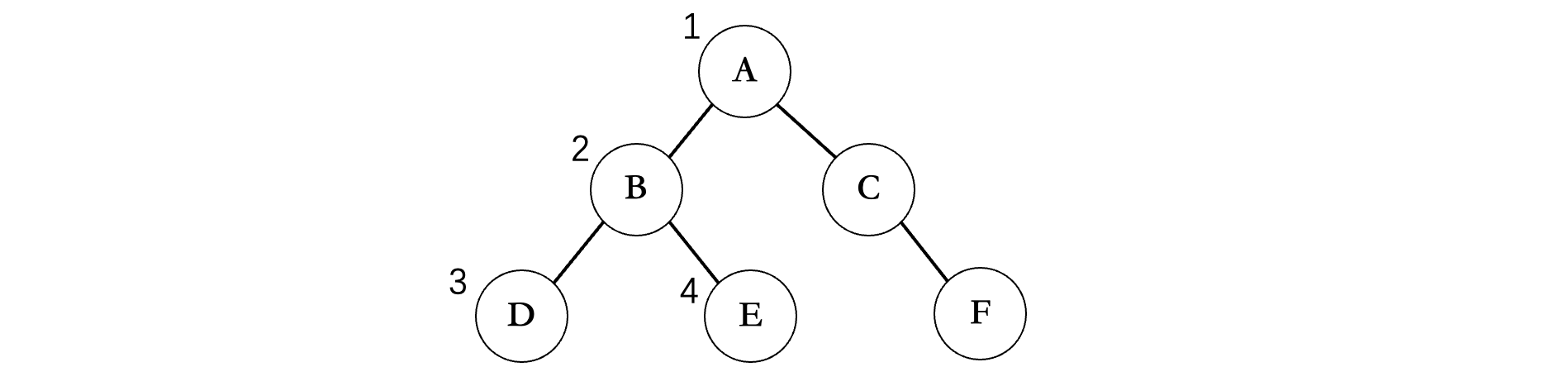
image-20220806171431845

从A开始，先左后右，那么下一个就是B，然后继续走左边，是D，现在ABD走完之后，B的左边结束了，那么就要开始B的右边了，所以下一个是E，E结束之后，现在A的左子树已经全部遍历完成了，然后就是右边，接着就是C，C没有左子树了，那么只能走右边了，最后输出F，所以上面这个二叉树的前序遍历结果为：ABDECF

  1. 打印根节点
  2. 前序遍历左子树
  3. 前序遍历右子树

我们不难发现规律，整棵二叉树（包括子树）的根节点一定是出现在最前面的，比如A在最前面，A的左子树根结点B也是在最前面的。我们现在就来尝试编写一下代码实现一下，先把二叉树构建出来：

public static void main(String[] args) {
    TreeNode<Character> a = new TreeNode<>('A');
    TreeNode<Character> b = new TreeNode<>('B');
    TreeNode<Character> c = new TreeNode<>('C');
    TreeNode<Character> d = new TreeNode<>('D');
    TreeNode<Character> e = new TreeNode<>('E');
    TreeNode<Character> f = new TreeNode<>('F');
    a.left = b;
    a.right = c;
    b.left = d;
    b.right = e;
    c.right = f;
}

组装好之后，我们来实现一下前序遍历的方法：

private static <T> void preOrder(TreeNode<T> root){
    System.out.print(root.element + " ");   //首先肯定要打印，这个是必须的
}

打印完成之后，我们就按照先左后右的规则往后遍历下一个结点，这里我们就直接使用递归来完成：

private static <T> void preOrder(TreeNode<T> root){
    System.out.print(root.element + " ");
    preOrder(root.left);    //先走左边
    preOrder(root.right);   //再走右边
}

不过还没完，我们的递归肯定是需要一个终止条件的，不可能无限地进行下去，如果已经走到底了，那么就不能再往下走了，所以：

private static <T> void preOrder(TreeNode<T> root){
    if(root == null) return;
    System.out.print(root.element);
    preOrder(root.left);
    preOrder(root.right);
}

最后我们来测试一下吧：

public static void main(String[] args) {
    ...
    preOrder(a);
}

可以看到结果为：

image-20220806173227580

这样我们就通过一个简单的递归操作完成了对一棵二叉树的前序遍历，如果不太好理解，建议结合调试进行观察。

那么前序遍历我们了解完了，接着就是中序遍历了，中序遍历在顺序上与前序遍历不同，前序遍历是走到哪就打印到哪，而中序遍历需要先完成整个左子树的遍历后再打印，然后再遍历其右子树。

我们还是以上面的二叉树为例：

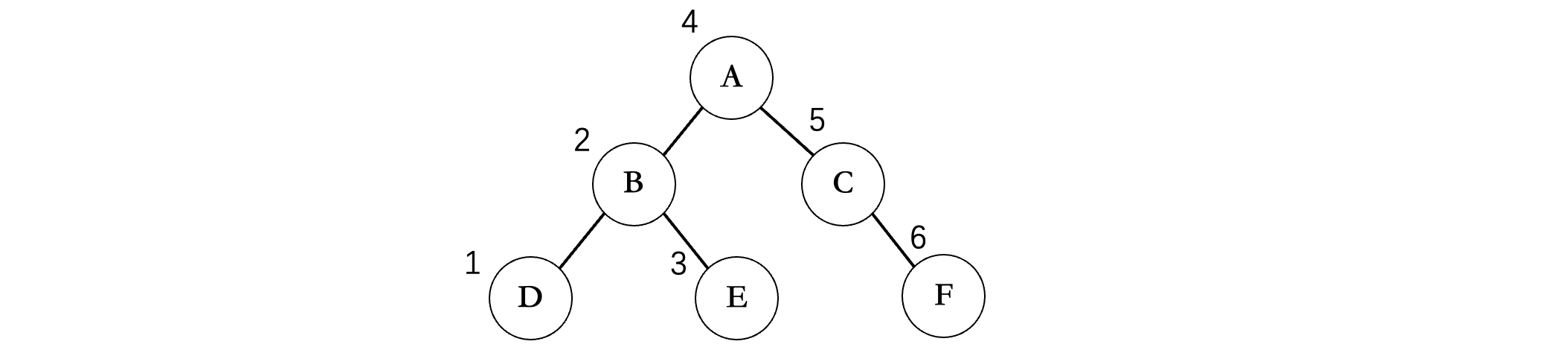
image-20220806230603967

首先需要先不断遍历左子树，走到最底部，但是沿途并不进行打印，而是到底之后，再打印，所以第一个打印的是D，接着由于没有右子树，所以我们回到B，此时再打印B，然后再去看B的右结点E，由于没有左子树和右子树了，所以直接打印E，左边遍历完成，接着回到A，打印A，然后对A的右子树重复上述操作。所以说遍历的基本规则还是一样的，只是打印值的时机发生了改变。

  1. 中序遍历左子树
  2. 打印结点
  3. 中序遍历右子树

所以这棵二叉树的中序遍历结果为：DBEACF，我们可以发现一个规律，就是在某个结点的左子树中所有结点，其中序遍历结果也是按照这样的规律排列的，比如A的左子树中所有结点，中序遍历结果中全部都在A的左边，右子树中所有的结点，全部都在A的右边（这个规律很关键，后面在做一些算法题时会用到）

那么怎么才能将打印调整到左子树全部遍历结束之后呢？其实很简单：

private static <T> void inOrder(TreeNode<T> root){
    if(root == null) return;
    inOrder(root.left);    //先完成全部左子树的遍历
    System.out.print(root.element);    //等待左子树遍历完成之后再打印
    inOrder(root.right);    //然后就是对右子树进行遍历
}

我们只需要将打印放到左子树遍历之后即可，这样打印出来的结果就是中序遍历的结果了：

image-20220806231752418

这样，我们就实现了二叉树的中序遍历，实际上还是很好理解的。

接着我们来看一下后序遍历，后序遍历继续将打印的时机延后，需要等待左右子树全部遍历完成，才会去进行打印。

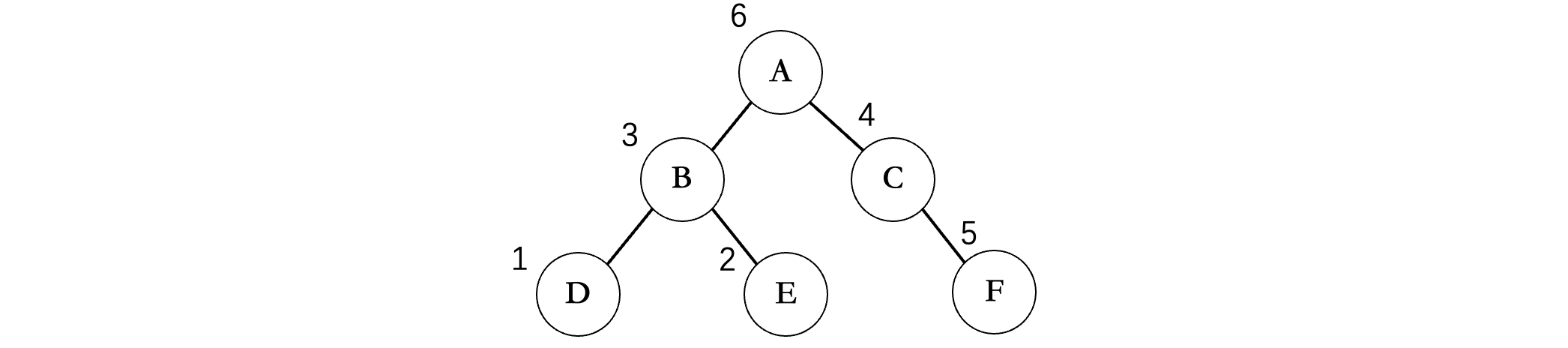
image-20220806233407910

首先还是一路向左，到达结点D，此时结点D没有左子树了，接着看结点D还有没有右子树，发现也没有，左右子树全部遍历完成，那么此时再打印D，同样的，D完事之后就回到B了，此时接着看B的右子树，发现有结点E，重复上述操作，E也打印出来了，接着B的左右子树全部OK，那么再打印B，接着A的左子树就完事了，现在回到A，看到A的右子树，继续重复上述步骤，当A的右子树也遍历结束后，最后再打印A结点。

  1. 后序遍历左子树
  2. 后序遍历右子树
  3. 打印结点

所以最后的遍历顺序为：DEBFCA，不难发现，整棵二叉树（包括子树）根结点一定是在后面的，比如A在所有的结点的后面，B在其子节点D、E的后面，这一点恰恰和前序遍历相反（注意不是得到的结果相反，是规律相反）

所以，按照这个思路，我们来编写一下后序遍历：

private static <T> void postOrder(TreeNode<T> root){
    if(root == null) return;
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.element);  //时机延迟到最后
}

结果如下：

image-20220806234428922

最后我们来看层序遍历，实际上这种遍历方式是我们人脑最容易理解的，它是按照每一层在进行遍历：

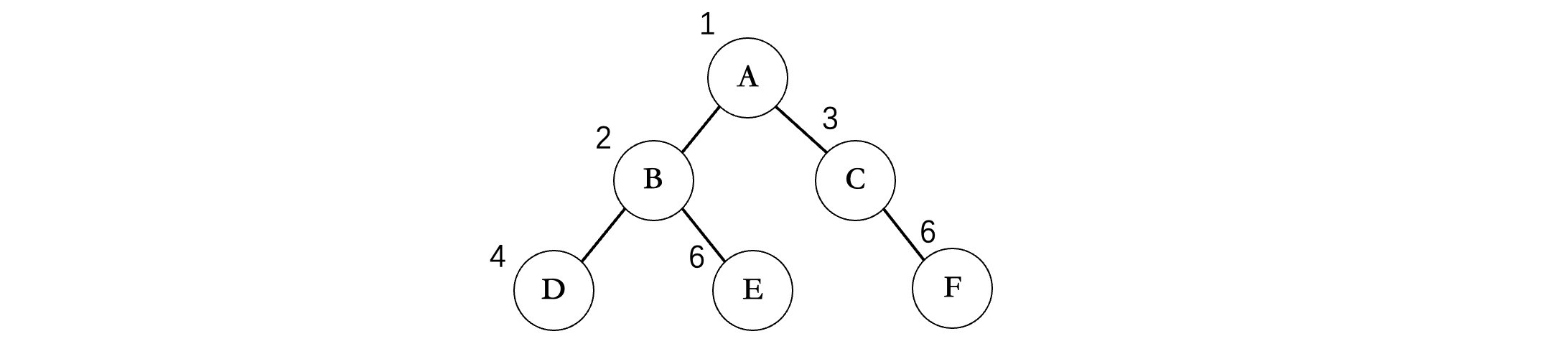
image-20220807205135936

层序遍历实际上就是按照从上往下每一层，从左到右的顺序打印每个结点，比如上面的这棵二叉树，那么层序遍历的结果就是：ABCDEF，像这样一层一层的挨个输出。

虽然理解起来比较简单，但是如果让你编程写出来，该咋搞？是不是感觉有点无从下手？

我们可以利用队列来实现层序遍历，首先将根结点存入队列中，接着循环执行以下步骤：

  • 进行出队操作，得到一个结点，并打印结点的值。
  • 将此结点的左右孩子结点依次入队。

不断重复以上步骤，直到队列为空。

我们来分析一下，首先肯定一开始A在里面：

image-20220807211522409

接着开始不断重复上面的步骤，首先是将队首元素出队，打印A，然后将A的左右孩子依次入队：

image-20220807211631110

现在队列中有B、C两个结点，继续重复上述操作，B先出队，打印B，然后将B的左右孩子依次入队：

image-20220807211723776

现在队列中有C、D、E这三个结点，继续重复，C出队并打印，然后将F入队：

image-20220807211800852

我们发现，这个过程中，打印的顺序正好就是我们层序遍历的顺序，所以说队列还是非常有用的，这里我们可以直接把之前的队列拿来用。那么现在我们就来上代码吧，首先是之前的队列：

public class LinkedQueue<E> {

    private final Node<E> head = new Node<>(null);

    public void offer(E element){
        Node<E> last = head;
        while (last.next != null)
            last = last.next;
        last.next = new Node<>(element);
    }

    public E poll(){
        if(head.next == null)
            throw new NoSuchElementException("队列为空");
        E e = head.next.element;
        head.next = head.next.next;
        return e;
    }
    
    public boolean isEmpty(){   //这里多写了一个判断队列为空的操作，方便之后使用
        return head.next == null;   //直接看头结点后面还有没有东西就行了
    }

    private static class Node<E> {
        E element;
        Node<E> next;

        public Node(E element) {
            this.element = element;
        }
    }
}

我们来尝试编写一下层序遍历：

private static <T> void levelOrder(TreeNode<T> root){
    LinkedQueue<TreeNode<T>> queue = new LinkedQueue<>();  //创建一个队列
    queue.offer(root);    //将根结点丢进队列
    while (!queue.isEmpty()) {   //如果队列不为空，就一直不断地取出来
        TreeNode<T> node = queue.poll();   //取一个出来
        System.out.print(node.element);  //打印
        if(node.left != null) queue.offer(node.left);   //如果左右孩子不为空，直接将左右孩子丢进队列
        if(node.right != null) queue.offer(node.right);
    }
}

可以看到结果就是层序遍历的结果：

image-20220807215630429

image-20220807215630429

前序和中序和后序遍历代码

package DataStructure;

public class Tree<E> {
    public E element;
    public Tree<E> left, right;

    public Tree(E element) {
        this.element = element;
    }

    //前序遍历
    public static <T> void preOrder(Tree<T> root) {
        if (root == null) return;
        System.out.print(root.element);
        preOrder(root.left);
        preOrder(root.right);
    }

    //中序遍历
    public static <T> void inOrder(Tree<T> root) {
        if (root == null) return;
        inOrder(root.left);    //先完成全部左子树的遍历
        System.out.print(root.element);    //等待左子树遍历完成之后再打印
        inOrder(root.right);    //然后就是对右子树进行遍历
    }

    //后序遍历
    public static <T> void postOrder(Tree<T> root) {
        if (root == null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.element);  //时机延迟到最后
    }
}

中序遍历代码

package DataStructure;

import java.util.NoSuchElementException;
//层序遍历
public class LinkedinOrderQueue<E> {

    private final Node<E> head = new Node<>(null);

    public void offer(E element) {
        Node<E> last = head;
        while (last.next != null)
            last = last.next;
        last.next = new Node<>(element);
    }

    public E poll() {
        if (head.next == null)
            throw new NoSuchElementException("队列为空");
        E e = head.next.element;
        head.next = head.next.next;
        return e;
    }

    public boolean isEmpty() {   //这里多写了一个判断队列为空的操作，方便之后使用
        return head.next == null;   //直接看头结点后面还有没有东西就行了
    }

    private class Node<E> {
        E element;
        Node<E> next;

        public Node(E element) {
            this.element = element;
        }
    }

    public static <T> void levelOrder(Tree<T> root) {
        LinkedinOrderQueue<Tree<T>> queue = new LinkedinOrderQueue<>();  //创建一个队列
        queue.offer(root);    //将根结点丢进队列
        while (!queue.isEmpty()) {   //如果队列不为空，就一直不断地取出来
            Tree<T> node = queue.poll();   //取一个出来
            System.out.print(node.element);  //打印
            if (node.left != null) queue.offer(node.left);   //如果左右孩子不为空，直接将左右孩子丢进队列
            if (node.right != null) queue.offer(node.right);
        }
    }
    /*
    上面这段代码是一个实现LinkedQueue的静态类，实现了队列的基本操作offer(添加元素)、poll(取出元素)和isEmpty(判断队列是否为空)。
    LinkedQueue类中也实现了一个levelOrder方法，用于实现树的层序遍历，它首先创建一个队列，
    然后将根结点放进队列中，然后判断队列是否为空，不为空则取出一个结点，
    并打印，然后判断左右孩子是否为空，不为空就放进队列中，重复这个过程直到队列为空。
     */
}

Main代码

import DataStructure.Tree;

import static DataStructure.LinkedinOrderQueue.levelOrder;
import static DataStructure.Tree.*;

public class Main {
    public static void main(String[] args) {
        Tree<Character> a = new Tree<>('A');
        Tree<Character> b = new Tree<>('B');
        Tree<Character> c = new Tree<>('C');
        Tree<Character> d = new Tree<>('D');
        Tree<Character> e = new Tree<>('E');
        Tree<Character> f = new Tree<>('F');
        a.left = b;
        a.right = c;
        b.left = d;
        b.right = e;
        c.right = f;

        System.out.print("前序遍历: ");
        preOrder(a);
        System.out.println();
        System.out.print("中序遍历: ");
        inOrder(a);
        System.out.println();
        System.out.print("后序遍历: ");
        postOrder(a);
        System.out.println();
        System.out.print("层序遍历: ");
        levelOrder(a);

    }
}
posted @ 2023-02-22 02:28  Wo_OD  阅读(17)  评论(0)  编辑  收藏  举报