Python之Numpy的基础及进阶函数(图文)
一样,咱的计算机还是得先拥有Python,并且安装了Numpy库。有疑问的话可以看这里呦~~~~
下面开讲:
NumPy的主要对象是齐次多维数组。它是一个元素表(通常是数字),并且都是相同类型,由正整数的元组索引。
其他暂且略过,咱主要说一些可以听懂的并且有实际效用的。
首先,我们得创建有一个ndarry对象,简单地介绍其中三种方法吧:
-
-
- a=np.array([1,2,3])
-

-
-
- data=[[1,2,3],[4,5,6]]
a=np.array(data)
- data=[[1,2,3],[4,5,6]]
-

-
-
- a=np.arange(15).reshape(3,5)
-

在这里我们就用第三个作为例子接着往下讲哈(我就不用再创建了哈哈)
ndarray对象的重要的属性如下:
-
- ndarray.ndim:
输出ndarray的维度(轴数,也有人叫它等级,在Python世界中,维度的数量被称为等级),这里的轴也叫坐标轴。
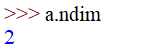
 这两种写法都是可以的,亲试如图,下面的其他函数也是一样的。
这两种写法都是可以的,亲试如图,下面的其他函数也是一样的。
例如,array([1,2,1])是一个等级为1的数组,因为它具有一个坐标轴,该轴的长度为3。
在上面的示例中,该数组的排名为2(它是2维的)。第一维(轴)的长度为3,第二维的长度为5。
-
- ndarray.shape:
输出数组的尺寸,即(n,m)。
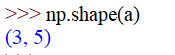
-
- ndarray.size:
数组元素的总数,即 n * m。
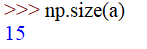
-
- ndarray.dtype:
数组中元素的数据类型,可进行转换。(这个一般默认float64 和 int32,你们可以自己多试试)

-
- ndarray.itemsize:
数组中每个元素的字节大小。(例子中则为 int 32/8 = 4,相当于ndarray.dtype.itemsize)
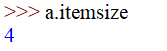
-
- ndarray.data:
该缓冲区包含数组的实际元素。(这个我们一般不用,我们都是用索引的QAQ)

还有好多,我就不一一截图了,懒。。。。。。
- np.zeros(10) #长度为10的0数组
- np.zeros((3,6)) #创建3行6列的0数组(注意有两个括号)
- np.ones(5)
- np.ones((3,4))
- np.arange(10)
- np.eye(3) # 3*3单位矩阵
- np.identity(3) # 3*3单位矩阵
- np.zeros_like(a) #创建与a相同行、列的全0矩阵
- np.ones_like(a) #创建与a相同行、列的全1矩阵
索引和切片类
- a1=a[0:1] ##这个切片的大有学问了,写的话大概得另起一篇了,有空再说
- a[0:1]=1 ##a变化后,a1的值也随之变化
- a1[0:1]=2 #a1变化后,a的值也随之变化
- a1=a[0:1].copy() #完全拷贝,值变化不影响a (和上面对比一下你就清楚了)
计算类
- a*a #每个元素平方(这个强!!!挺好用的。)
- a*5 #每个元素乘以5
- a.mean() #数据均值
- a.sum() #数组和
- a.sum(axis=0) #按列求和
- a.sum(axis=1) #按行求和
- a.sort() #对a进行排序(这个也是好东西啊~~~)
- a.sort(1) #0按行排序,1按列排序
- np.sort(a,0) #a按行排序(本身不发生变化!!!!!!)
- x.dot(y) ##矩阵x与y相乘
- np.in1d(a,[2,3,6]) #value中的每一个值是否在[2,3,6]中(如果是,该值返回true,否则返回false.)
- np.in1d([2,3,6],a)
- np.in1d(x,y)
- np.intersect1d(x,y) #返回x和y中的交集,并返回有序结构
- np.union1d(x,y) #计算x,y的并集,并返回有序结构
- np.setdiff1d(x,y) #集合的差,即在x中且不在y中
- samples=np.random.normal(size=(4,4)) #产生4维正态分布矩阵
- from numpy.linalg import * #计算与矩阵相关,行列式,矩阵的逆等
- np.linalg.det(samples) #矩阵行列式
- np.linalg.inv(samples) #矩阵求逆
- np.diag(samples) #返回矩阵对角线元素
- np.linalg.eig(samples) #返回矩阵特征值和特征向量
- import timeit #导入计算时间的模块
- np.save('some_a',a) #保存文件
- np.load("some_a.py") #读取磁盘保存数据
- a=np.loadtxt("code_public.txt",delimiter=',') #读取文本数据
- arr=np.loadtxt("d:\code\arr.txt",delimiter=',') #读取d盘数据
行吧,时间也差不多了,我都写累了,相信你也看累了,是时候去 stzb 看看了。
一个佛系的博客更新者,随手写写,看心情吧 (っ•̀ω•́)っ✎⁾⁾


 浙公网安备 33010602011771号
浙公网安备 33010602011771号