过原点的两向量\(u\)与向量\(v\)垂直相当于点\(a\)到点\(b\)的距离与点\(a\)到点\(-b\)的距离相等，也即它们的距离的平方相等。
计算点\(a\)到点\(-b\)的距离：
\(\begin{align} [distance(a,-b)]^2&=\lVert u-(-v)\rVert ^2=\lVert u+v\rVert ^2\\ &=(u+v)\cdot(u+v)\\ &=u\cdot(u+v)+v\cdot(u+v)\\ &=u\cdot u+u\cdot v+v\cdot u+v\cdot v\\ &=\lVert u\rVert^2+\lVert v\rVert ^2 +2u\cdot v\\ \end{align}\)
将\(-b\)与\(b\)互换：
\(\begin{align} [distance(a,b)]^2&=\lVert u\rVert^2+\lVert -v\rVert ^2 +2u\cdot (-v)\\ &=\lVert u\rVert^2+\lVert v\rVert ^2 -2u\cdot v\\ \end{align}\)
两个距离平方相等的充分必要条件是：\(2u\cdot v=-2u\cdot v\)，即\(u\cdot v=0\)。
如果\(u\cdot v=0\)，则向量\(u\)和向量\(v\)是（相互）正交的，这两个向量在空间中（相互）垂直。
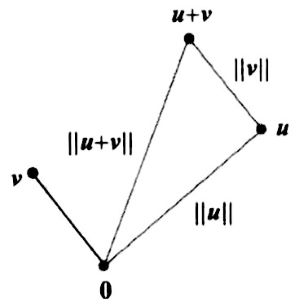
两个向量\(u\)和\(v\)正交的充分必要条件是\(\lVert u+v\rVert ^2=\lVert u\rVert ^2+ \lVert v\rVert ^2\)（勾股定理）。
