极坐标系
定义
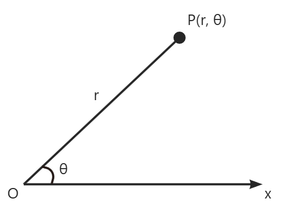
以极点\(O\)引一条射线做极轴\(Ox\)，选定长度单位、角度单位（一般为弧度）及正方向（一般为逆时针），\(\lvert OP\rvert\)为点\(P\)的极径，记为\(r\)，角\(xOP\)为点\(P\)的极角，记为\(\theta\)，有序对\((r,\theta)\)叫做点\(P\)的极坐标，记为\(P(r,\theta)\)。
极坐标与直角坐标的转换
极坐标转换至直角坐标：
\(x=r\cos(\theta)\)（相当于\(r\)朝\(x\)轴投影）
\(y=r\sin(\theta)\)（相当于\(r\)朝\(y\)轴投影）
直角坐标转换至极坐标：
\(r=\sqrt{x^2+y^2}\)
\(\tan(\theta)=\frac{y}{x}(x\ne0)\)
球坐标系
定义
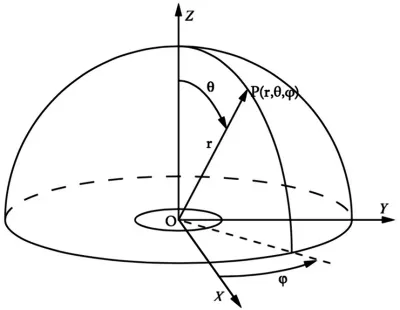
\(\vert OP\vert\)为点\(P\)到原点的距离，记为\(r\)，\(OP\)与\(Z\)轴构成的夹角为点\(P\)的极角，记为\(\theta\)，\(OP\)在\(XY\)平面的投影与\(X\)轴构成的夹角为点\(P\)的方位角，记为\(\varphi\)，有序对\((r,\theta,\varphi)\)叫做点\(P\)的球坐标，记为\(P(r,\theta,\varphi)\)，球坐标可视为极坐标的三维推广。
球坐标与直角坐标的转换：
球坐标转换至直角坐标：
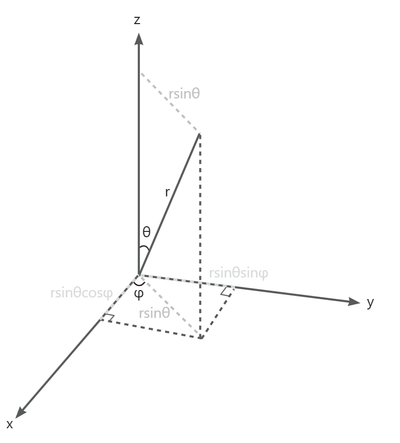
\(x=r\sin(\theta)\cos(\varphi)\)（相当于\(r\)先朝\(xy\)平面投影再朝\(x\)轴投影）
\(y=r\sin(\theta)sin(\varphi)\)（相当于\(r\)先朝\(xy\)平面投影再朝\(y\)轴投影）
\(z=r\cos(\theta)\)（相当于\(r\)朝\(z\)轴投影）
直角坐标转换至球坐标：
\(r=\sqrt{x^2+y^2+z^2}\)
\(\theta=\arccos(\frac{z}{r})=\arcsin\left(\frac{\sqrt{x^2+y^2}}{r}\right)=\arctan\left(\frac{\sqrt{x^2+y^2}}{z}\right)\)
\(\varphi=\arccos\left(\frac{x}{r\sin(\theta)}\right)=\arcsin\left(\frac{y}{r\sin(\theta)}\right)=\arctan\left(\frac{y}{x}\right)\)
计算\(\varphi\)时：
- 必须依照\((x,y)\)所处的象限来计算正确的反正切值。
- 当\(x=0\)时，判断\(y\)的值：
若\(y>0\)，则\(\varphi=\frac{\pi}{2}\)
若\(y<0\)，则\(\varphi=-\frac{\pi}{2}\)或\(\frac{3\pi}{2}\)
若\(y=0\)，则\(\varphi\)为未定值（因为\(\frac{0}{0}\)为未定式）。
半球积分
沿方位角\(\varphi\)方向移动的弧对应的半径为\(r\sin(\varphi)\)，对其弧长的微分等于\(r\sin\theta d\varphi\)，沿极角\(\theta\)方向移动的弧对应的半径为\(r\)，对其弧长的微分等于\(rd\theta\)，则球面面积微分\(dA=r^2\sin\theta d\theta d\varphi\)
可得半球积分：
\(\int_0^{2\pi}\int_0^\frac{\pi}{2}r^2\sin\theta d\theta d\varphi\)
