立体角
立体角,常用字母Ω表示,是一个物体对特定点的三维空间的角度,是平面角在三维空间中的类比。它描述的是站在某一点的观察者测量到的物体大小的尺度。例如,对于一个特定的观察点,一个在该观察点附近的小物体有可能和一个远处的大物体有着相同的立体角。
平面角的大小可以用弧度(radian)表示,立体角的大小可以用球面度(steradian)表示。
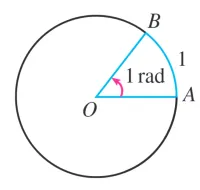
弧度
长度等于半径的圆弧所对的平面角为1弧度(radian),弧度是弧长和半径的比值,描述的是单位圆上的一段弧长。
在半径为\(r\)的圆中,弧长为\(l\)的弧所对应的弧度为\(\alpha\ rad\),那么\(\lvert \alpha \rvert=\frac{l}{r}\)。
由圆的周长\(2\pi r\)可得整个圆的弧度是\(2\pi\)。
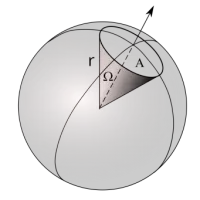
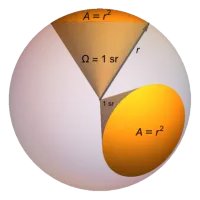
球面度
面积等于半径平方的球冠[1]所对的立体角为1球面度(steradian),球面度是球冠和半径平方的比值,描述的是单位球上的一块面积。
在半径为\(r\)的球中,球冠面积为\(A\)的球冠所对应的球面度为\(\omega\ sr\),那么\(\lvert\omega\rvert=\frac{A}{r^2}\)。
由球的面积为\(4\pi r^2\)可得整个球的球面度为\(4\pi\)。
一段圆弧绕经过它的一个端点的直径旋转所成的曲面叫做球冠。 ↩︎



