切线空间
法线纹理用来呈现物体表面的凹凸细节,模型顶点自身的法线定义于模型空间(Object Space)中,模型的法线纹理一般存储在模型顶点的切线空间(Tangent Space)中,一般的,顶点本身为切线空间原点,选择顶点法线方向
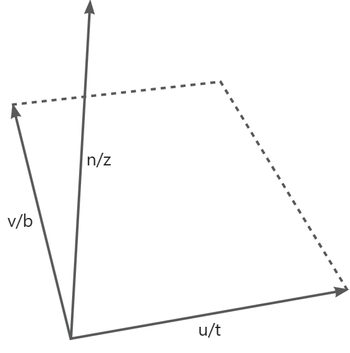
可以通过三角形顶点的位置和其UV坐标推导出切线方向
由此可见:
将上式写为矩阵形式:
对
通过对
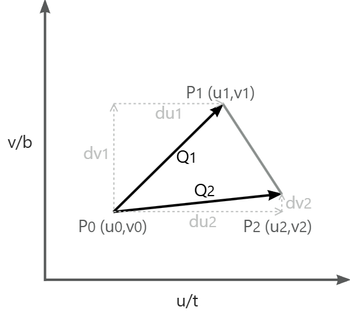
因为三角面是一个平面,只需要计算一个三角面的切线和副切线即可,它们对于三角形的顶点来说都是一样的,被多个三角面共享的顶点只需要将多个结果平均化即可。
采样计算
存储与采样
纹理颜色
法线非统一缩放问题
在模型变换时,跟顶点相关的信息也需要一并变换,其中包括法线与切线等,由切线空间部分可知顶点的切线通过顶点之间的差值计算得来,根据线性变换的性质,用于顶点变换的矩阵
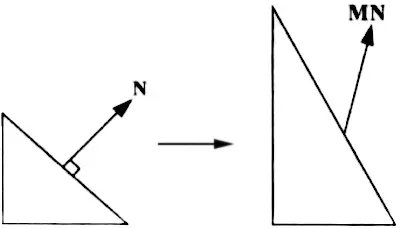
因为切线向量
将
由此可见
由于
若
在世界空间中采样计算法线
在顶点着色器中计算世界空间下的法线向量 normalWS 、切线向量 tangentWS 和副切线向量 bitangentWS ,在计算 normalWS 时,变换顶点到世界空间的矩阵
half3 normalWS = normalize(mul(input.normalOS, (float3x3)unity_WorldToObject));
half3 tangentWS = normalize(mul((float3x3)UNITY_MATRIX_M, input.tangentOS.xyz));
half3 bitangentWS = cross(normalWS, tangentWS) * input.tangentOS.w;
在片元着色器中采样切线空间下的法线向量 normalTS ,由于纹理格式存在差异,使用Shader Lab中内置函数 UnpackNormal() 对存储的法线进行反映射,然后使用顶点着色器传入的切线向量 tangentWS 、副切线向量 bitangentWS 和法线向量构成变换矩阵
half3 normalTS = UnpackNormal(tex2D(_NormalMap, input.uv));
half3x3 tangentToWorld = half3x3(input.tangentWS.xyz, input.bitangentWS.xyz, input.normalWS.xyz);
half3 normalWS = mul(normalTS.xyz, tangentToWorld);
Unity中的切线设置
Unity默认使用 MikkTSpace 计算切线,在Model Import Settings中可进行设置。
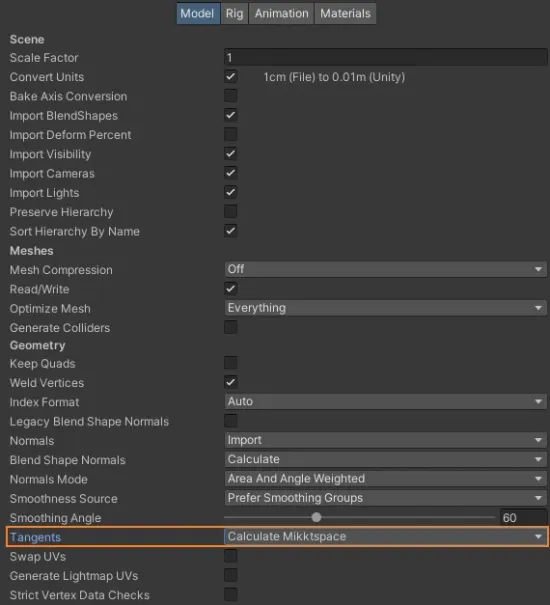
切线最常用于凹凸贴图着色器中。切线是单位长度的矢量,它顺着网格表面沿水平 (U) 纹理方向。Unity 中的切线表示为 Vector4, 其“x,y,z”分量定义矢量,而 w 用于在需要时翻转副法线。Unity 计算另一个表面矢量(副法线)的方法是获取法线与切线之间的叉积,然后将结果乘以切线的 w。因此,w 应始终为 1 或 -1。
参考
《3D游戏与计算机图形学中的数学方法》
《Unity Shader入门精要》






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)