点积

公式

1. \(u\cdot v=\sum_{i=1}^nu_iv_i\)
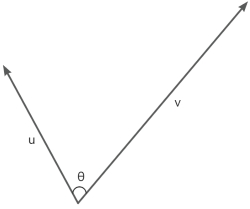
2. \(u\cdot v=\lVert u\rVert\lVert v\rVert\cos\theta\) ，若\(u\)，\(v\)是单位向量则\(u\cdot v=\cos\theta\)
3. \(\theta=\arccos\left(\frac{u\cdot v}{\lVert u\rVert\lVert v\rVert}\right)\)，若\(u\)，\(v\)是单位向量则\(\theta=\arccos\left(u\cdot v\right)\)

推导

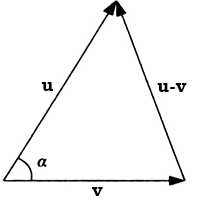
根据余弦定理，可知
\(\lVert u-v\rVert^2=\lVert u\rVert^2+\lVert v\rVert^2-2\lVert u\rVert\lVert v\rVert\cos\alpha\)
展开可得
\(\sum_{i=1}^n(u_i-v_i)^2=\sum_{i=1}^nu_i^2+\sum_{i=1}^nv_i^2-2\lVert u\rVert\lVert v\rVert\cos\alpha\)
即
\(\sum_{i=1}^nu_i^2-2\sum_{i=1}^nu_iv_i+\sum_{i=1}^nv_i^2=\sum_{i=1}^nu_i^2+\sum_{i=1}^nv_i^2-2\lVert u\rVert\lVert v\rVert\cos\alpha\)
两边消去\(\sum_{i=1}^nu_i^2+\sum_{i=1}^nv_i^2\)，同时两边除以-2，得
\(\sum_{i=1}^nu_iv_i=\lVert u\rVert\lVert v\rVert\cos\alpha\)

投影

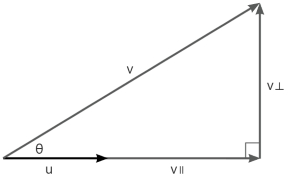
由图中可得

\(\cos\theta=\frac{\lVert v_\parallel\rVert}{\lVert v\rVert}\)，即\(\lVert v_\parallel\rVert=\cos\theta\lVert v\rVert\)

两边同乘\(\lVert u\rVert\)，得

\(\lVert u\rVert\lVert v_\parallel\rVert=\cos\theta\lVert u\rVert\lVert v\rVert\)，即\(u\cdot v\)

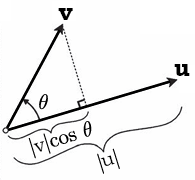
如此，可将\(u\)与\(v\)的点积看作\(v\)在\(u\)上的投影模长与\(u\)的模长的乘积，或\(u\)在\(v\)上的投影模长与\(v\)的模长的乘积。

线性变换

亦可从线性变换的角度理解，如将向量看作1行n列的矩阵，由于此矩阵导致的维度压缩致使向量被变换到一维数轴上。

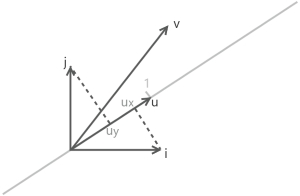
如二维平面中的向量\(v\)可以由其基向量表示为\(v_xi+v_yj\)，假设有一个线性变换将\(i\)和\(j\)分别变换到与\(u\)同方向数轴上的点\(u_x\)与\(u_y\)，若将\(v\)变换到这条数轴上，等同于分解为\(v_x\cdot u_x+v_y\cdot u_y\)，也即线性变换\(\begin{bmatrix}u_x & u_y\end{bmatrix}\begin{bmatrix}v_x \\v_y\end{bmatrix}\)。

应用

点积结果越大，两向量越相近

u·v	θ	向量u和向量v
>0	0°≤θ＜90°	方向大致相同
=0	θ≤90°	正交（垂直）
<0	90°＜θ≤180°	方向基本相反