虚数的引入
\(x^2=-1\Rightarrow x=\pm\sqrt{-1}=\pm i\)
一个实数的平方不可能为\(-1\),故引入虚数单位\(i\),使\(i^2=-1\)
复数的两种表示
坐标表示:
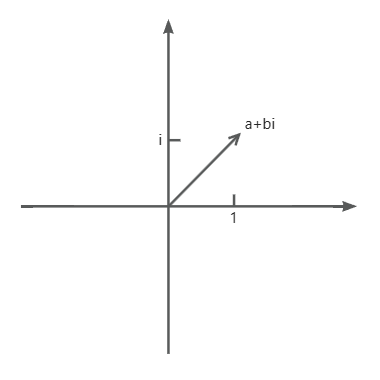
\(Z=a+bi\)
三角函数表示:
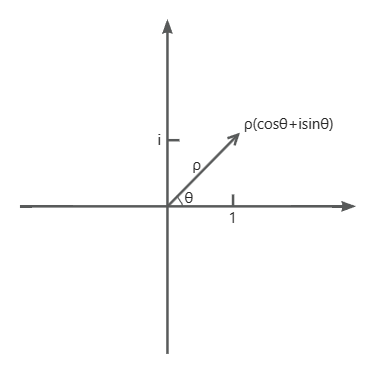
\(a=\rho cos\theta, b=\rho sin\theta \Rightarrow Z=\rho(cos\theta+isin\theta)\)
复数的乘法
模相乘,角相加
\(\begin{align}
Z_1Z_2&=\rho_1(cos\theta_1+isin\theta_1)\rho_2(cos\theta_2+isin\theta_2)\\
&=\rho_1\rho_2[(cos\theta_1cos\theta_2-sin\theta_1sin\theta_2)+i(sin\theta_1cos\theta_2+cos\theta_1sin\theta_2)]//两角和公式\\
&=\rho_1\rho_2[cos(\theta_1+\theta_2)+isin(\theta_1+\theta_2)]
\end{align}\)
由两复数相乘的最终结果可以看出两个复数的乘法为两者的模相乘,辐角相加
乘以i旋转90度
\(i\)用三角函数表示为:
\(i=cos\frac{\pi}{2}+isin\frac{\pi}{2}\)
当一个复数乘以i,相当于辐角增加\(\frac{\pi}{2}\),即逆时针旋转90度:
\(Zi=\rho[cos(\theta+\frac{\pi}{2})+isin(\theta+\frac{\pi}{2})]\)
\(e^x\)的特性
\(\frac{d(e^x)}{dx}=e^x\)
函数\(e^x\)的导数为其本身,即其变化率等于其本身,其越大其增长率便越大
\(e^0=1\)
欧拉公式
\(\frac{d(e^{i\theta})}{d\theta}=ie^{i\theta}\)
\(e^{i\theta}\)的变化率\(ie^{i\theta}\)相当于其本身大小逆时针旋转90度
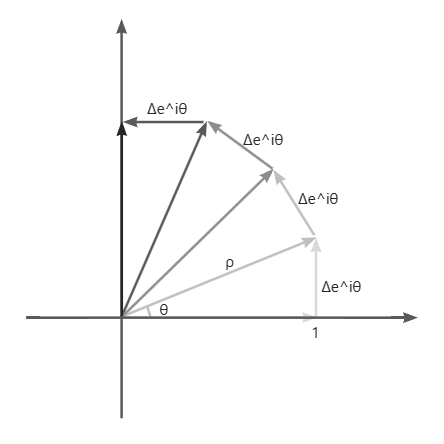
\(\theta\)初始值为0,此时\(e^{i\theta}=1\),每当\(\theta\)发生变化产生增量\(\Delta e^{i\theta}\)时,\(e^{i\theta}\)变化率\(ie^{i\theta}\)的方向与其方向垂直,变化后新的\(e^{i\theta}\)沿圆周运动,当\(\theta\)继续产生变化后,新的变化率\(ie^{i\theta}\)与其依然垂直,\(e^{i\theta}\)继续沿圆周运动
某一时刻的\(e^{i\theta}\)可表示为\(e^{i\theta}=cos\theta+isin\theta\quad(\rho=1)\)
欧拉公式应用
- 当\(\theta=\pi\)时,\(e^{i\pi}=-1, e^{i\pi}e^{i\pi}=e^{i2\pi}\Rightarrow(-1)(-1)=1\)
- \(e^{a+bi}=e^ae^{bi}=e^a(cosb+isinb)\\ x^{a+bi}=(e^{lnx})^{a+bi}=e^{alnx+bilnx}\)
- \(ln(a+bi)=ln(\rho e^{i\theta})=ln\rho+i\theta\)
- \(\begin{cases} e^{i\theta}=cos\theta+isin\theta\\ e^{-i\theta}=cos\theta-isin\theta\\ \end{cases} \Rightarrow \begin{cases} sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}\\ cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}\\ \end{cases}\)



