《数据结构》_7搜索树
二叉搜索树
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。中序遍历二叉搜索树,会得到一个以节点关键字的值递增排列的有序序列。
二叉搜索树基本运算的实现,借鉴:https://blog.csdn.net/yanxiaolx/article/details/51986428
二叉平衡树
平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列,可以参考Fibonacci(斐波那契)数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
平衡树是为了避免二叉搜索数退化成链表而出现的,而且可以说,任务完成得很出色。
二叉平衡树运算的实现,借鉴https://www.cnblogs.com/suimeng/p/4560056.html
首先需要了解一个概念:平衡因子——左子树的高度减右子树的高度,取值只可能为0,1,-1。
数据结构的定义
typedef char KeyType; //关键字 typedef struct MyRcdType //记录 { KeyType key; }RcdType,*RcdArr; typedef enum MyBFStatus //为了方便平衡因子的赋值,这里进行枚举 { //RH,EH,LH分别表示右子树较高,左右子树等高,左子树较高 RH,EH,LH }BFStatus; typedef struct MyBBSTNode //树结点类型定义 { RcdType data; //数据成员 BFStatus bf; //平衡因子 struct MyBBSTNode *lchild,*rchild; //左右分支 }BBSTNode,*BBSTree;
插入:
在插入时需要注意的问题是插入可能会导致失衡,此时就需要通过旋转最小失衡子树进行恢复平衡 。
最小失衡子树:在新插入的节点向上查找,以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的,如下。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
分为四种需要调整的情况:
1.LL型:如果BL的平衡因子为1,且新节点插入BL的左子树上,则单向向右旋转,调整以B为根的子树,树的高度不变,返回OK。
/* * 当T的左子树的左子树上的节点使得T的平衡度为2时,以T为中心进行右旋。 */ bool LLRotate(BiTree *T) { BiTree lc; lc = (*T)->lchild; (*T)->lchild = lc->rchild; lc->rchild = (*T); //注意要更新结点的高度。整个树中只有*T的左子树和lc的右子树发生了变化,所以只需更改这两棵树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; lc->height = max(GetHeight(lc->lchild), GetHeight(lc->rchild)) + 1; *T = lc; return true; }
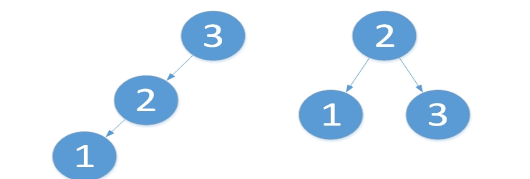
2.LR型:如果的平衡因子为-1,且新插入的结点在右子树上,参考平衡树的原则,对以B为根的子树进行调整,树的高度不变,返回OK。
要分为两步进行旋。旋转之后为“原来根结点的左孩子的右孩子作为新的根结点”。
第一以较高子树的根,即1,为中心向左旋转。具体步骤如下。
i. 将2的左子树作为1的右子树(维护树的有序性,只是此处为NULL而已)
ii. 将1作为2的左子树
iii. 将2作为3的左子树

第二以原树的根,即3为中心,向右旋转。最后结果如下

旋转后,1,2,3的平衡因子变为0(无需记忆)。
/* * 当T的左子树的右子树上的节点使得T的平衡度为2时, * 先以T的左子树为中心进行左旋,再以T为中心进行右旋。 */ bool LRRotate(BiTree *T) { RRRotate(&((*T)->lchild)); LLRotate(T); return true; }
3.RR型
。旋转的步骤如下。旋转之后为“原来根结点的右孩子作为新的根结点”。
i. 将2作为根结点
ii. 将1作为2的左孩子
iii. 将2的左孩子作为1的右孩子(维护树的有序性,只是此处为NULL而已)
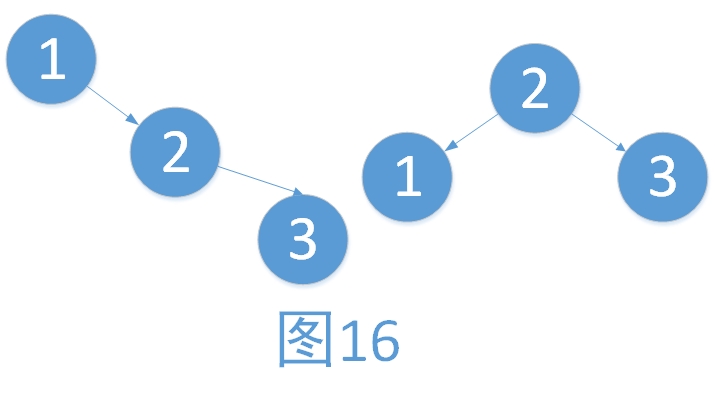
最后1,2,3的平衡因子都为EH。
/* * 当T的右子树的右子树上的节点使得T的平衡度为-2时,以T为中心进行左旋。 */ bool RRRotate(BiTree *T) { BiTree rc; rc = (*T)->rchild; (*T)->rchild = rc->lchild; rc->lchild = (*T); //注意要更新结点的高度。整个树中只有*T的左子树和lc的右子树发生了变化,所以只需更改这两棵树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; rc->height = max(GetHeight(rc->lchild), GetHeight(rc->rchild)) + 1; *T = rc; return true; }
4.RL型
与LR型类似,我们需要进行两次旋转。旋转之后为“原来根结点的右孩子的左孩子作为新的根结点”。
第一,以根结点的右孩子即3为中心向右旋转,结果如下。具体步骤如下
i. 将2作为1的右孩子
ii. 将3作为2的右孩子
iii. 将2的右孩子作为3的左孩子(维护树的有序性,只是此处为NULL而已)

第二,以原根结点即1,作为中心,向左旋转。结果如下。具体步骤如下
i. 将2作为根结点
ii. 将1作为2的左孩子
iii. 将2的左孩子作为1的右孩子(维护树的有序性,只是此处为NULL而已)

/* * 当T的右子树的左子树上的节点使得T的平衡度为-2时, * 先以T的右子树为中心进行右旋,再以T为中心进行左旋。 */bool RLRotate(BiTree *T){ LLRotate(&((*T)->rchild)); RRRotate(T); return true;
总的插入操作代码:
/* * 插入操作。 * 如果以*T为根结点的二叉平衡树中已有结点key,插入失败,函数返回FALSE; * 否则将结点key插入到树中,插入结点后的树仍然为二叉平衡树,函数返回TRUE。 */ bool AVLInsert(BiTree *T, TElemType key) { BiTree t; //如果当前查找的根结点为空树,表明查无此结点,故插入结点。 if (!*T) { t = (BiTree)malloc(sizeof(BiNode)); t->data = key; t->height = 1; t->lchild = NULL; t->rchild = NULL; *T = t; return true; } //已有此结点,不再插入。 else if (key == (*T)->data) { return false; } //在左子树中递归插入。 else if (key < (*T)->data) { if (!AVLInsert(&((*T)->lchild), key)) return false; else { //插入成功,修改树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; //已在*T的左子树插入结点key,判断是否需要进行旋转以保持二叉平衡树的特性。 if (2 == GetHeight((*T)->lchild) - GetHeight((*T)->rchild)) { //在左子树的左子树中插入结点。 if (GetHeight((*T)->lchild->lchild) > GetHeight((*T)->lchild->rchild)) { LLRotate(T); } //在左子树的右子树中插入结点。 else { LRRotate(T); } } return true; } } //在右子树中递归插入。 else // (key > (*T)->data) { if (!AVLInsert(&(*T)->rchild, key)) return false; else { //插入成功,修改树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; //已在*T的右子树插入结点key,判断是否需要进行旋转以保持二叉平衡树的特性。 if (-2 == GetHeight((*T)->lchild) - GetHeight((*T)->rchild)) { //在右子树的左子树中插入结点。 if (GetHeight((*T)->rchild->lchild) > GetHeight((*T)->rchild->rchild)) { RLRotate(T); } //在右子树的右子树中插入结点。 else { RRRotate(T); } } return true; } } }
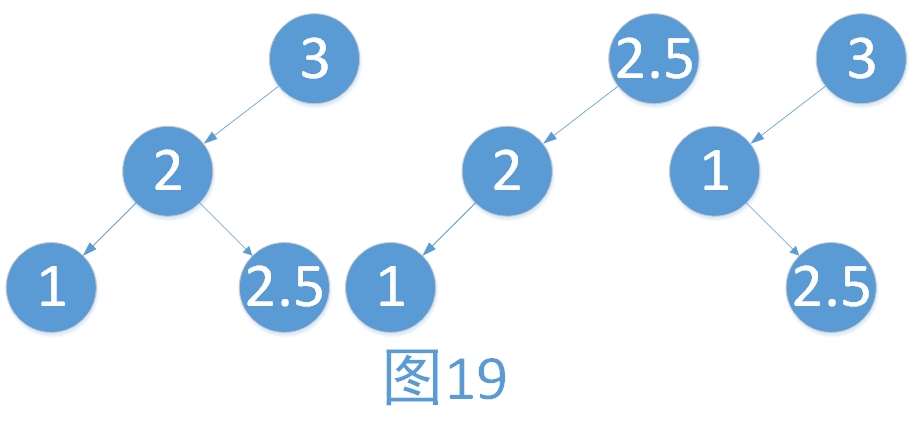
假如有一棵二叉查找树如下,我们对它进行中序遍历,可以得到1, 2, 2.5, 3。我们发现,这是一个递增的序列。假如我们现在要删除的结点为3,在不考虑树的平衡问题时,应该哪个结点来作为顶替3的位置呢呢?答案是:对排序二叉树进行中序遍历时,3的直接前驱或者直接后驱。在这里,就是2.5,所以删除后,不进行调整的结果如中间图。假如我们现在要删除的结点为2,在不考虑树的平衡问题时,1顶替2的位置(假设左孩子优先于右孩子)。最后如下右图。
具体的步骤如下:
i. 寻找到要删除的结点(3)
ii. 将待删除结点的直接前驱或者直接后驱赋值给待删除结点(2.5赋值给3结点)
iii. 将直接前驱或者直接后驱删除(将叶子结点的2.5删除)
由于我们今天主要讲的是平衡二叉树的平衡调整,所以这部分就权当给读者恶补一下。假如读者还是不能理解,请先查看一下二叉查找树的删除,再继续往下看。
2. 平衡因子的预告
我们已经知道,平衡因子有且仅有三种取值,LH,RH,EH。对于如下的一棵树,删除一个结点后
a) 原本树左右子树等高。根平衡因子的取值变化为EH->LH,EH->RH。
b) 原本树左右子树不等高,在较高的子树上进行删除,根平衡因子的取值变化为LH->EH,RH->EH。需要注意的是,当根的平衡因子变化为LH->EH,RH->EH时整棵树的高度是下降的。最简单的例子如下。以下两棵树,分别删除1,3后,平衡因子LH->EH,RH->EH。最后树的高度都下降了。

c) 原本树左右子树不等高,在较低的子树上进行删除,此时需要对树进行平衡处理。如下删除了结点1,得到右边的不平衡树。

3. 什么会导致树高降低
a) 如第2点的的第b项,根的平衡因子由LH->EH,RH->EH时整棵树的高度是下降的。
b) 建立在a点以及平衡处理正确的基础上,对树进行正确的平衡处理后,树高会降低。为什么呢?因为其实最小不平衡子树进行旋转后,最小不平衡子树根的平衡因子总是变
为EH,或者说,平衡调整总是降低了最小不平衡子树的高度。举例如下。树的高度由原来的3变为了2.

二、 正式进入AVL树的删除与调整
1. 删除结点导致平衡二叉树失衡
AVL树也是一棵二叉查找树,所以它的删除也是建立在二叉查找树的删除之上的,只是,我们需要在不平衡的时候进行调整。而我们在预备知识的第2点中的C项中已经提及到,假如我们在较低的子树上进行删除,将会直接导致不平衡树的出现。那么,我们需要进行平衡处理的,就在于此种情况。举个栗子。
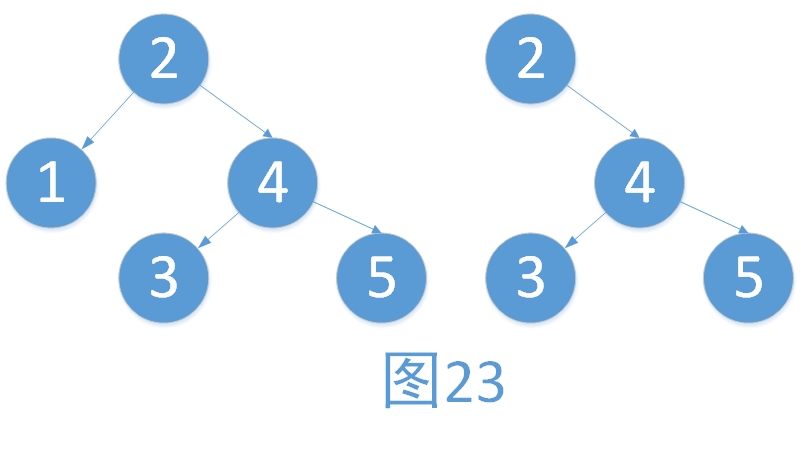
2. 调整不平衡子树后,导致了更大的不平衡子树
假设最小不平衡子树为A,它为双亲结点b的左子树,而b的平衡因子为RH。假设我们现在对A进行了平衡处理,如上所讲,进行平衡处理将导致树高降低。即我们让b较矮的子树变得更矮了。此时对于b而言,同样也是不平衡的。此时,我们需要再一次进行一次平衡处理。举个栗子如下。
假设我们删除了结点6.那么最小不平衡子树就是1,3,5对应的二叉树。它的双亲10的平衡因子为RH。我们首先对最小不平衡子树进行调整,结果如右图。我们发现,最小不平衡子树从根结点的左子树变成了整棵树,所以这个时候我们又要进行一次平衡调整。具体的平衡调整步骤与插入时是一致的,在这里就赘述。
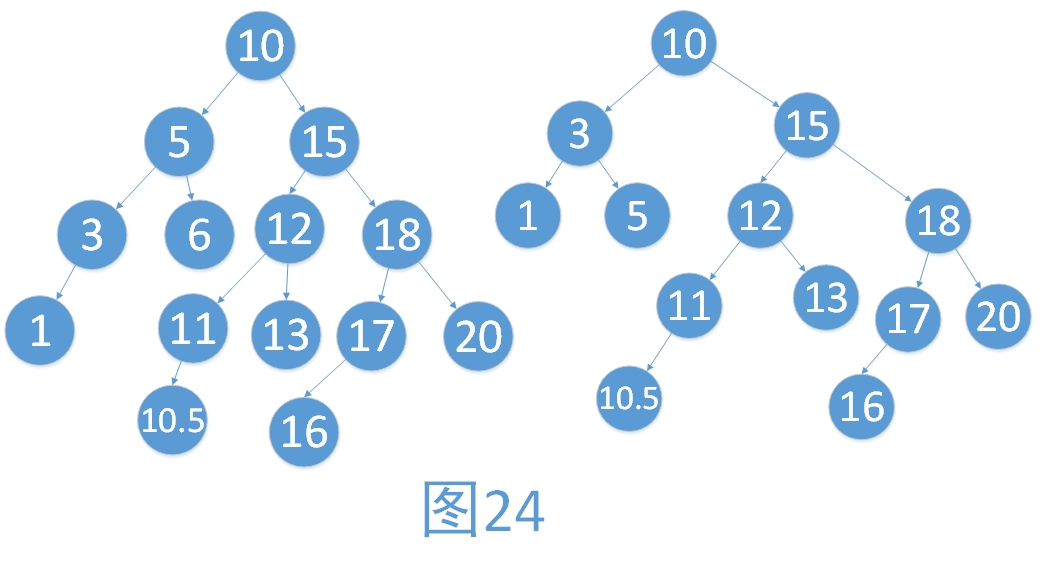
在讲解插入新的结点进行平衡时,说到删除时与插入时不有着很大的不同就在于此。插入时,进行一次平衡处理,整棵树都会处于平衡状态,而在删除时,需要进行多次平衡处理,才能保证树处于平衡状态。
细心的朋友可能发现,上面右图中,最小不平衡子树的较高子树的平衡因子为EH。这个时候,就出现了前面插入时提及的不可能出现的失衡情况。
3. 失衡与调整的最后一种情况LE与RE
LE与RE型的失衡树,在进行调整的时候,和LL与RR型的旋转方式是一致的。只是最后初始根结点的平衡因子不为EH而已。就拿上面的例子而言,调整后的结果如下。初始根结点的平衡因子为RH。相对应的,假如是LE的情况,调整后初始根结点的平衡因子为LH。

/* * 删除操作。 * 如果以*T为根结点的树中存在结点key,将结点删除,函数返回TRUE, * 否则删除失败,函数返回FALSE。 */ bool AVLDelete(BiTree *T, TElemType key) { BiTree pre, post; //没有找到该结点。 if (!*T) return false; //找到结点,将它删除。 else if (key == (*T)->data) { //待删除节点为叶子结点。 if (!(*T)->lchild && !(*T)->rchild) *T = NULL; //待删除结点只有右孩子。 else if (!(*T)->lchild) *T = (*T)->rchild; //待删除结点只有左孩子。 else if (!(*T)->rchild) *T = (*T)->lchild; //待删除结点既有左孩子,又有右孩子。 else { //当待删除结点*T左子树的高度大于右子树的高度时,用*T的前驱结点pre代替*T, //再将结点pre从树中删除。这样可以保证删除结点后的树仍为二叉平衡树。 if (GetHeight((*T)->lchild) > GetHeight((*T)->rchild)) { //寻找前驱结点pre。 pre = (*T)->lchild; while (pre->rchild) { pre = pre->rchild; } //用pre替换*T。 (*T)->data = pre->data; //删除节点pre。 //虽然能够确定pre所属最小子树的根结点为&pre, //但是不采用AVLDelete(&pre,pre->data)删除pre,目的是方便递归更改节点的高度。 AVLDelete(&((*T)->lchild), pre->data); } //当待删除结点*T左子树的高度小于或者等于右子树的高度时,用*T的后继结点post代替*T, //再将结点post从树中删除。这样可以保证删除结点后的树仍为二叉平衡树。 else { //寻找后继节点post。 post = (*T)->rchild; while (post->lchild) post = post->lchild; //用post替换*T。 (*T)->data = post->data; //删除节点post。 //虽然能够确定post所属最小子树的根结点为&post, //但是不采用AVLDelete(&post,post->data)删除post,目的是方便递归更改节点的高度。 AVLDelete(&((*T)->rchild), post->data); } } return true; } //在左子树中递归删除。 else if (key < (*T)->data) { if (!AVLDelete(&((*T)->lchild), key)) return false; else { //删除成功,修改树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; //已在*T的左子树删除结点key,判断是否需要进行旋转以保持二叉平衡树的特性。 if (-2 == GetHeight((*T)->lchild) - GetHeight((*T)->rchild)) { if (GetHeight((*T)->rchild->lchild) > GetHeight((*T)->rchild->rchild)) { RLRotate(T); } else { RRRotate(T); } } return true; } } //在右子树中递归删除。 else { if (!AVLDelete(&((*T)->rchild), key)) return false; else { //删除成功,修改树的高度。 (*T)->height = max(GetHeight((*T)->lchild), GetHeight((*T)->rchild)) + 1; //已在*T的右子树删除结点key,判断是否需要进行旋转以保持二叉平衡树的特性。 if (2 == GetHeight((*T)->lchild) - GetHeight((*T)->rchild)) { if (GetHeight((*T)->lchild->lchild) > GetHeight((*T)->lchild->rchild)) { LLRotate(T); } else { LRRotate(T); } } return true; } } }

B-树
展示一个4阶的B-树
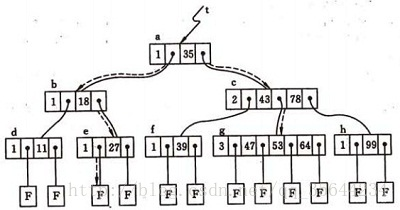
B-树的基本操作–查找介绍
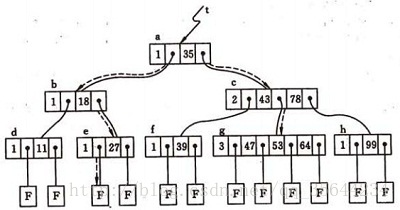
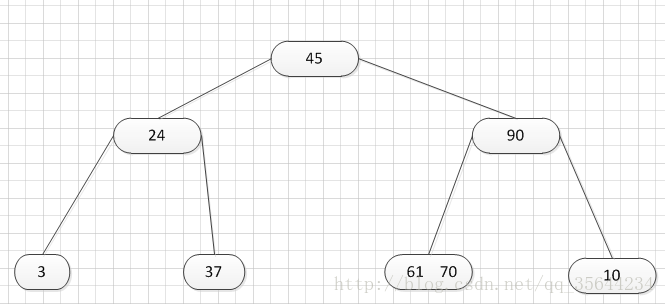
我们先给出如下的一个4阶的B-树结构。
如上图所示,这是我们的一个4阶的B-树,现在假设我们需要查找45这个数是否在B-树中。
- 从根节点出发,发现根节点a有1个关键字为35,其中45>35,往右子树走,进入节点c
- 发现结点c有2个关键字,其中其中43<45<78,所以进入结点g。
- 发现结点g有3个关键字,其中3<45<47,所以继续往下走,发现进入了结束符结点:F,所以45不在B-树中
B-树的查找过程为:
- 在B- 树中查找结点
- 在结点中查找关键字。
由于B- 树通常存储在磁盘上, 则前一查找操作是在磁盘上进行的, 而后一查找操作是在内存中进行的, 即
在磁盘上找到指针p 所指结点后, 先将结点中的信息读入内存, 然后再利用顺序查找或折半查找查询等于K
的关键字。显然, 在磁盘上进行一次查找比在内存中进行一次查找的时间消耗多得多.
因此, 在磁盘上进行查找的次数、即待查找关键字所在结点在B- 树上的层次树, 是决定B树查找效率的首要
因素,对于有n个关键字的m阶B-树,从根结点到关键字所在结点的路径上路过的结点数不超过:
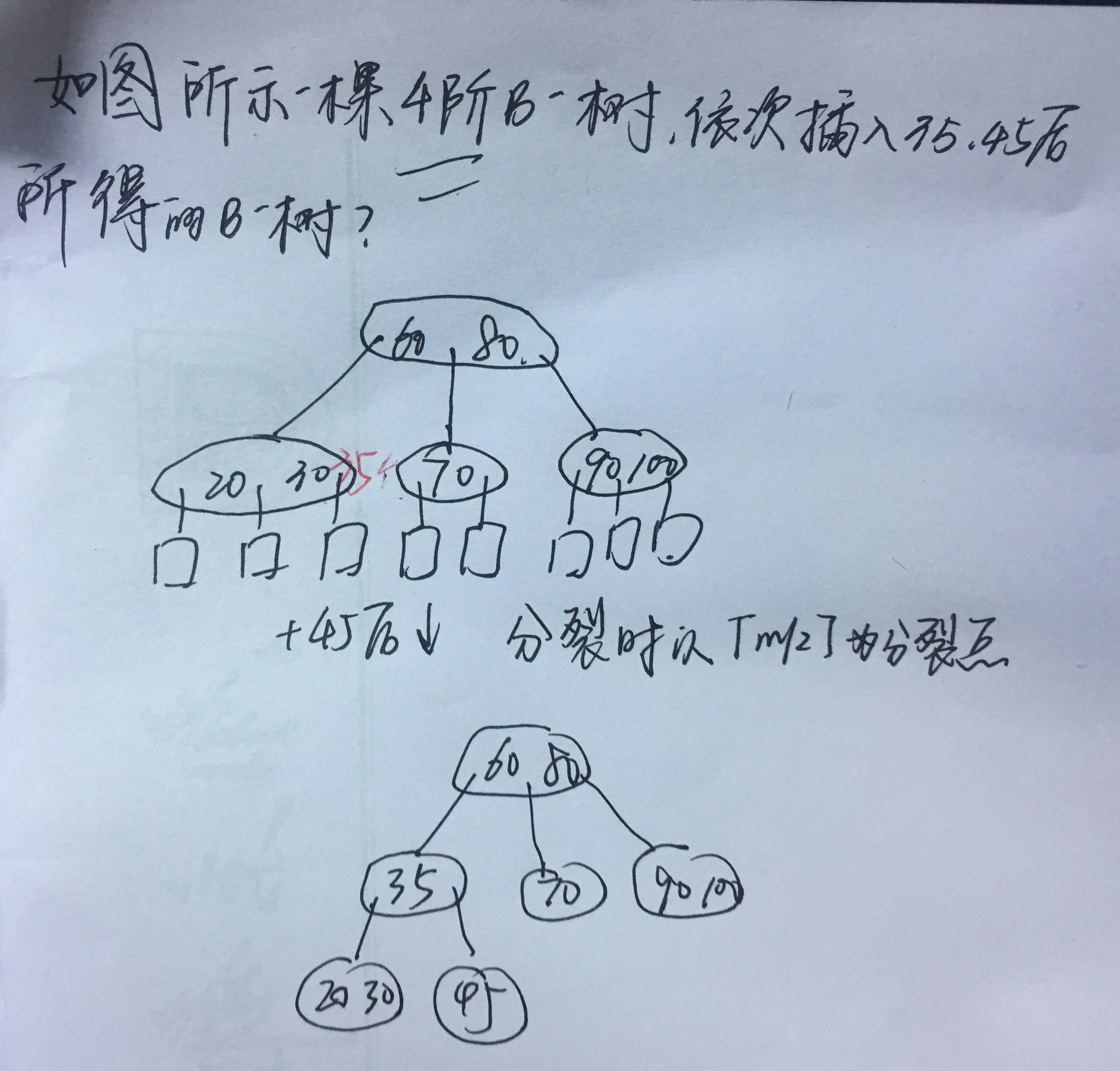
B-树的插入
1. 使用查找算法查找出关键字的插入位置,如果在B-树中查找到了关键字,则直接返回。
2.判断终端结点上的关键字数量是否满足:n<=m-1,如果满足的话,在该终端结点上添加一个关键字,否则需要产生结点的“分裂”。
分裂的方法是:生成一新结点。把原结点上的关键字和k(需要插入的值)按升序排序后,从中间位置把关键字(不包括中间位置的关键字)分成两部分。左部分所含关键字放在旧结点中,右部分所含关键字放在新结点中,中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过(m-1),则要再分裂,再往上插。直至这个过程传到根结点为止。
下面我们来举例说明,首先假设这个B-树的阶为:3。树的初始化时如下:
首先,我需要插入一个关键字:30,可以得到如下的结果:
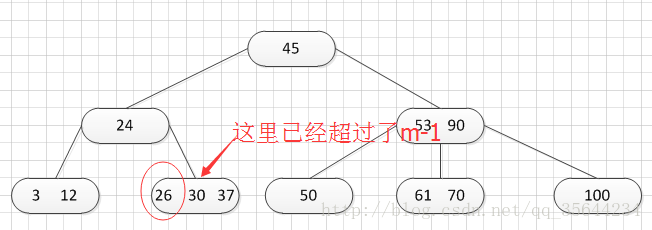
再插入26,得到如下的结果:
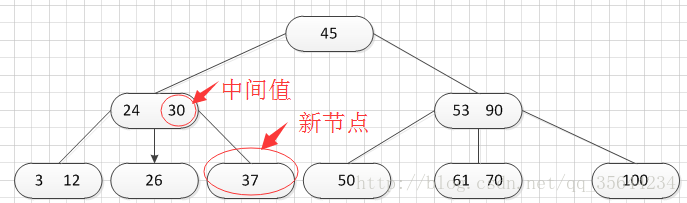
OK,此时如图所示,在插入的那个终端结点中,它的关键字数已经超过了m-1=2,所以我们需要对结点进分裂,所以我们先对关键字排序,得到:26 30 37 ,所以它的左部分为(不包括中间值):26,中间值为:30,右部为:37,左部放在原来的结点,右部放入新的结点,而中间值则插入到父结点,并且父结点会产生一个新的指针,指向新的结点的位置,如下图所示:
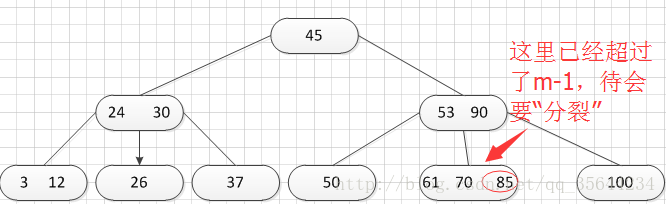
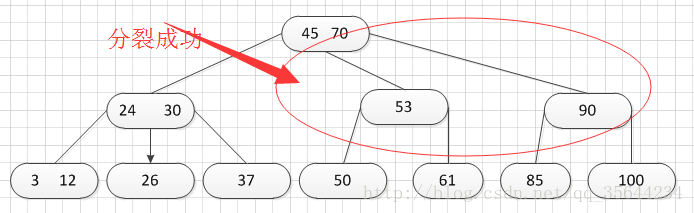
OK,然后我们继续插入新的关键字:85,得到如下图结果:
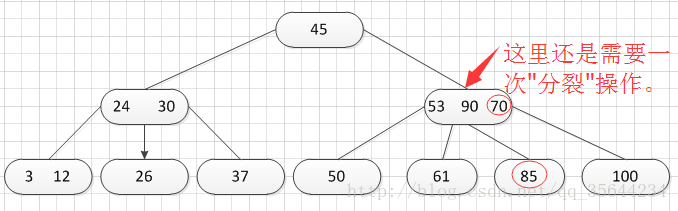
正如图所示,我需要对刚才插入的那个结点进行“分裂”操作,操作方式和之前的一样,得到的结果如下:
哦,当我们分裂完后,突然发现之前的那个结点的父亲结点的度为4了,说明它的关键字数超过了m-1,所以需要对其父结点进行“分裂”操作,得到如下的结果:
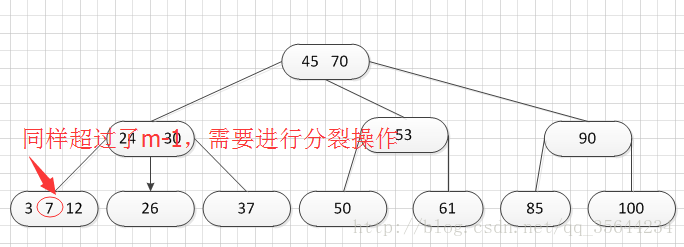
好,我们继续插入一个新的关键字:7,得到如下结果:
同样,需要对新的结点进行分裂操作,得到如下的结果: 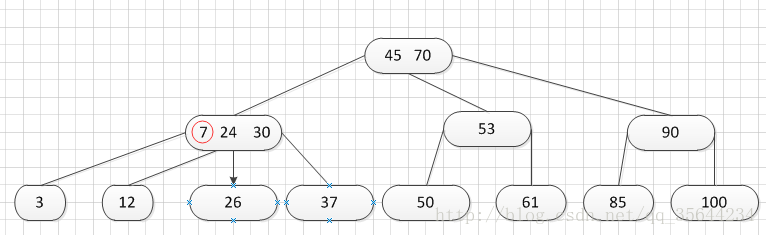
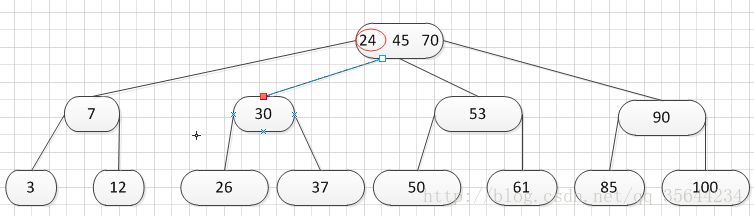
到了这里,我就需要继续对我们的父亲结点进行分裂操作,因为它的关键字数超过了:m-1.
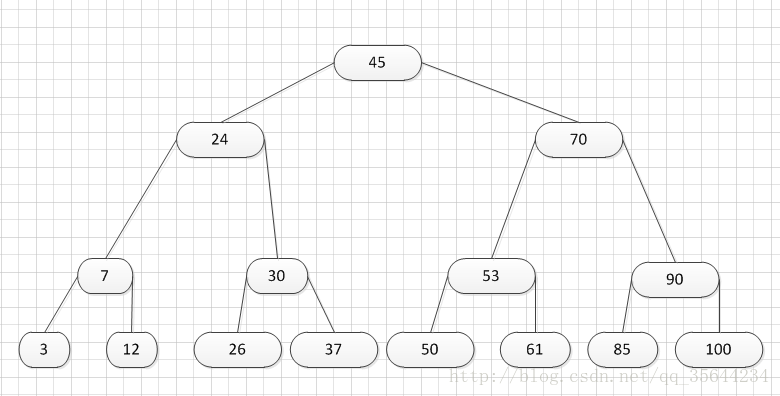
哦,终于遇到这种情况了,我们的根结点出现了关键子数量超过m-1的情况了,这个时候我们需要对父亲结点进行分列操作,但是根结点没父亲啊,所以我们需要重新创建根结点了。
好了,到了这里我们也知道怎么进行B-树的插入操作。
5、B-树的删除操作
B-树的删除操作同样是分为两个步骤:
- 利用前述的B-树的查找算法找出该关键字所在的结点。然后根据 k(需要删除的关键字)所在结点是否为叶子结点有不同的处理方法。如果没有找到,则直接返回。
- 若该结点为非叶结点,且被删关键字为该结点中第i个关键字key[i],则可从指针son[i]所指的子树中找出最小关键字Y,代替key[i]的位置,然后在叶结点中删去Y。
如果是叶子结点的话,需要分为下面三种情况进行删除。
- 如果被删关键字所在结点的原关键字个数n>=[m/2] ( 上取整),说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单,只需删除对应的关键字:k和指针:A 即可。
- 如果被删关键字所在结点的关键字个数n等于( 上取整)[ m/2 ]-1,说明删去该关键字后该结点将不满足B-树的定义,需要调整。
调整过程为:如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右兄弟(或左兄弟)结点中的关键字数目大于( 上取整)[m/2]-1。则可将右兄弟(或左兄弟)结点中最小关键字(或最大的关键字)上移至双亲结点。而将双亲结点中小(大)于该上移关键字的关键字下移至被删关键字所在结点中。
- 被删关键字所在结点和其相邻的兄弟结点中的关键字数目均等于(上取整)[m/2]-1。假设该结点有右兄弟,且其右兄弟结点地址由双亲结点中的指针Ai所指,则在删去关键字之后,它所在结点中剩余的关键字和指针,加上双亲结点中的关键字Ki一起,合并到 Ai所指兄弟结点中(若没有右兄弟,则合并至左兄弟结点中)。
下面,我们给出删除叶子结点的三种情况:
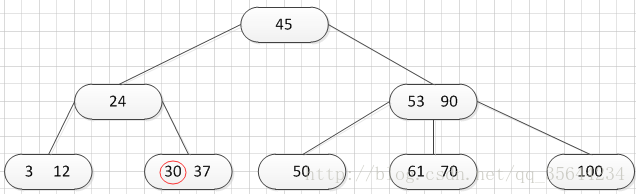
第一种:关键字的数不小于(上取整)[m/2],如下图删除关键字:12 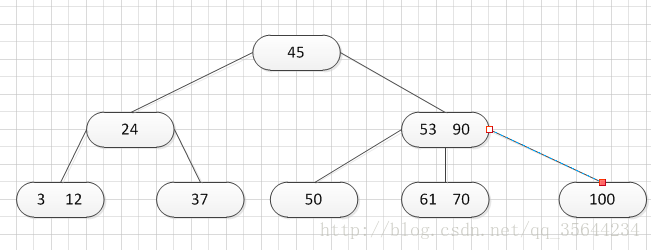
删除12后的结果如下,只是简单的删除关键字12和其对应的指针。
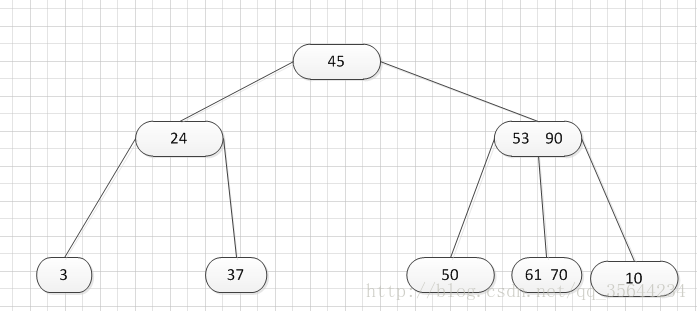
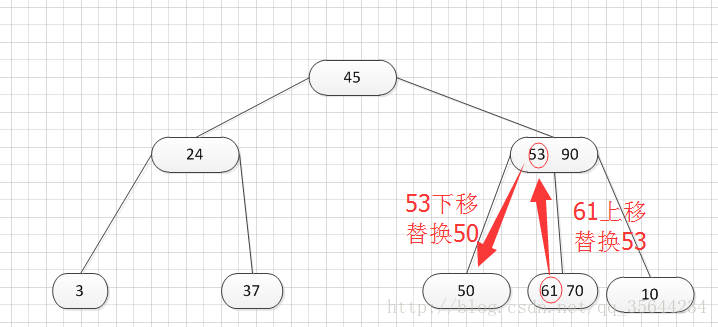
第二种:关键字个数n等于( 上取整)[ m/2 ]-1,而且该结点相邻的右兄弟(或左兄弟)结点中的关键字数目大于( 上取整)[m/2]-1。
如上图,所示,我们需要删除50这个关键字,所以我们需要把50的右兄弟中最小的关键字:61上移到其父结点,然后替换小于61的关键字53的位置,53则放至50的结点中。然后,我们可以得到如下的结果:
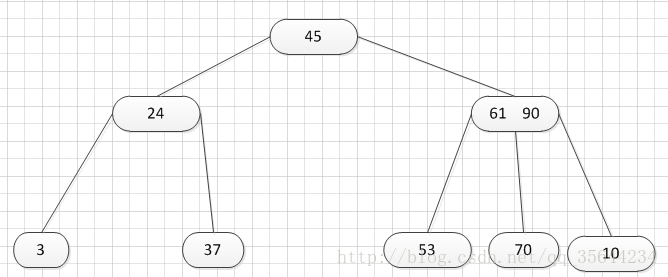
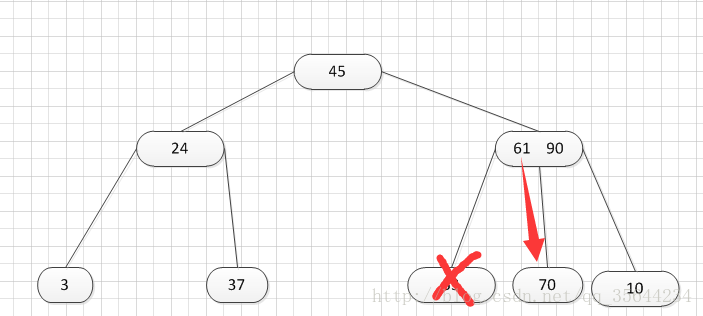
第三种:关键字个数n等于( 上取整)[ m/2 ]-1,而且被删关键字所在结点和其相邻的兄弟结点中的关键字数目均等于(上取整)[m/2]-1
如上图所示,我们需要删除53,那么我们就要把53所在的结点其他关键字(这里没有其他关键字了)和父亲结点的61这个关键字一起合并到70这个关键字所占的结点。得到如下所示的结果:
Ok,我已经分别对上述的四种删除的情况都做了举例,大家如果还有什么不清楚的,可以看看代码,估计就可以明白了
B-树的基本操作的代码实现
B-Tree.h
#ifndef BMT_H_ #define BMT_H_ #include<iostream> #include<cstdlib> using namespace std; #define m 3 typedef int KeyType; typedef struct BMTNode { int keynum; BMTNode * parent; KeyType key[m + 1]; BMTNode * ptr[m + 1]; BMTNode() : keynum(0), parent(NULL) { for (int i = 0; i <= m; ++i) { key[i] = 0; ptr[i] = NULL; }//endfor }//endctor }*BMT; typedef struct Node { int keynum; //关键字的数量 Node * parent; //父亲结点 KeyType key[m + 1]; //记录关键字,但是0号单元不用 Node * ptr[m + 1]; //记录孩子结点的指针 Node() :keynum(0), parent(NULL) { for (int i = 0; i <= m; i++) { key[i] = 0; ptr[i] = NULL; }//endfor }//endcontruct }; class BTree { private: Node * head; int search(Node *& T, KeyType K); //查找关键字 void insert(Node * & T, int i, KeyType K, Node * rhs); //插入关键字的位置 bool split(Node *& T, int s, Node * & rhs, KeyType & midK); //结点分裂 bool newroot(Node * & T, Node * & lhs, KeyType midK, Node * & rhs); void RotateLeft(Node * parent, int idx, Node * cur, Node * rsilb); void RotateRight(Node * parent, int idx, Node * cur, Node * lsilb); void Merge(Node * parent, int idx, Node * lsilb, Node * cur); void DeleteBalance(Node * curNode); void Delete(Node * curNode, int curIdx); public: BTree(); Node * gethead(); bool searchKey_BTree(KeyType K, Node * & recNode, int & recIdx); bool insert_BTree(KeyType k); bool Delete_BTree(KeyType K); void Destroy(Node * & T); void WalkThrough(Node * & T); }; #endif /* BMT_H_ */
B-Tree.cpp
#include"B-Tree.h" BTree::BTree() { this->head = NULL; } //结点中,查找关键字序列,是否存在k,私有方法 int BTree::search(Node * & t,KeyType k) { int i = 0; for (int j = 1; j <= t->keynum; ++j) { if (t->key[j] <= k) { i = j; } } return i; } //遍历整个树,查找对应的关键字,公有方法, bool BTree::searchKey_BTree(KeyType k, Node * & recNode, int & recIdx) { if (!head) { //cerr << "树为空" << endl; return false; } Node * p = head; Node * q = NULL; bool found = false; int i=0; while (p && !found) { i = this->search(p, k); //记住i返回两种情况:第一种是找到对应的关键字 //第二次是找到了最后一个小于k的关键字下标(主要作用与插入时) if (i > 0 && p->key[i] == k) { //找到了记录结点和结点中关键字的下标 recIdx = i; recNode = p; return true; }//endif else { recNode = p; // 记录p的值,方便返回 recIdx = i; p = p->ptr[recIdx]; // 查找下一个结点, }//endelse }//endw return false; } //这是在结点的关键字序列中,插入一个而关键字,私有方法 void BTree::insert(Node * & t, int i, KeyType k, Node * rhs) { //我们需要把关键字序列往后移动,然后插入新的关键字 for (int j = t->keynum; j >= i + 1; --j) { t->key[j + 1] = t->key[j]; t->ptr[j + 1] = t->ptr[j]; } //插入新的关键字 t->key[i + 1] = k; t->ptr[i + 1] = rhs; ++t->keynum; } //对对应的结点进行分裂处理,对t结点进行分裂处理,私有方法 bool BTree::split(Node * & t, int s, Node * & rhs, KeyType & midk) { rhs = new Node; //rhs为新建的结点,用于保存右半部分的。 if (!rhs) { overflow_error; return false; } //我们们把t分裂的,所以rhs是t的兄弟结点,有相同的父母 rhs->parent = t->parent; //其中关键字序列的中间值为 midk = t->key[s]; t->key[s] = 0; //这个通过画图,就可以知道rhs的0号孩子的指针,就是t的s号结点指针 rhs->ptr[0] = t->ptr[s]; //如果原来的t的s号孩子指针,现在的rhs的0号孩子指针不为空,则需要改变孩子的的父亲结点 if (rhs->ptr[0]) { rhs->ptr[0]->parent = rhs; }//endif t->ptr[s] = NULL; for (int i = 1; i <= m - s; ++i) { //现在是把右半部分全部复制到到rhs中 rhs->key[i] = t->key[s + i]; t->key[s + i] = 0; rhs->ptr[i] = t->ptr[s + i]; t->ptr[s + i] = NULL; //理由和刚才的理由一样 if (rhs->ptr[i]) { rhs->ptr[i]->parent = rhs; }//endif }//endfor rhs->keynum = m - s; t->keynum = s - 1; return true; } //新建一个新的结点,私有方法 bool BTree::newroot(Node * & t, Node * & lhs, KeyType midk, Node * & rhs) { Node * temp = new Node; if (!temp) { overflow_error; return false; } temp->keynum = 1; temp->key[1] = midk; temp->ptr[0] = lhs; //左孩子不为空 if (temp->ptr[0]) { temp->ptr[0]->parent = temp; } temp->ptr[1] = rhs; //右孩子不为空 if (temp->ptr[1]) { temp->ptr[1]->parent = temp; } t = temp; return true; } //插入一个k(public方法) bool BTree::insert_BTree(KeyType k) { Node * curNode = NULL; int preIdx = 0; if (this->searchKey_BTree(k, curNode, preIdx)) { cout << "关键已经存在" << endl; return false; } else { //没有找到关键字 KeyType curk = k; Node * rhs = NULL; bool finished = false; while (!finished && curNode) { //不管是否合法,直接先插入刚才找到的那个关键字序列中 this->insert(curNode, preIdx, curk, rhs); if (curNode->keynum < m) {//满足条件,直接退出 finished = true; } else { int s = (m + 1) / 2; //s为中间值的下标 if (!this->split(curNode, s, rhs, curk)) { //分裂失败,直接返回 return false; } if (curNode->parent == NULL) { //如果curNode已经是根节点了,则可以直接退出了 break; } else { //如果有那个父亲结点的话,此时curk指向的是原来这个结点中间值 //所以需要和父亲结点融合 curNode = curNode->parent; preIdx = this->search(curNode, curk); } } } //如果head为空树,或者根结点已经分裂为结点curNode和rhs了,此时是肯定到了 //根结点了 if (!finished && !this->newroot(head, curNode, curk, rhs)) { cerr << "failed to create new root" << endl; exit(EXIT_FAILURE); } } } //删除结点k,找到合适的结点(public方法) bool BTree::Delete_BTree(KeyType k) { Node * curNode = NULL; int curIdx = 0; if (this->searchKey_BTree(k, curNode, curIdx)) { this->Delete(curNode, curIdx); return true; } else { return false; } } //删除对应的进入结点,去删除关键字 void BTree::Delete(Node * curNode, int curIdx) { //curIdx不合法法时,直接返回 if (curIdx<0 || curIdx>curNode->keynum) { return; } while (true) {//这里的步骤不是很清楚,等下来讨论 //此时说明我们是处于非叶子结点 if (curNode->ptr[curIdx - 1] && curNode->ptr[curIdx]) { //使用右子树中最小的关键字替换对应当前的关键的,然后删除那个最小的关键字 Node * p1 = curNode->ptr[curIdx]; while (p1->ptr[0]) { p1 = p1->ptr[0]; } int res = p1->key[1]; this->Delete_BTree(p1->key[1]); curNode->key[curIdx] = res; break; } else if (!curNode->ptr[curIdx - 1] && !curNode->ptr[curIdx]) { // is leaf for (int i = curIdx; i <= curNode->keynum; ++i) { curNode->key[i] = curNode->key[i + 1]; // all ptr are NULL , no need to move. }//end for. --curNode->keynum; this->DeleteBalance(curNode); break; } else { //debug cerr << "Error" << endl; } }//endw } //删除对应关键字后,我们需要对删除后的树进行调整 void BTree::DeleteBalance(Node * curNode) { int lb = (int)m / 2; Node * parent = curNode->parent; while (parent && curNode->keynum < lb) {//说明删除了关键字后,原来的那个结点已经不 //符合B-树的最小结点要求,这个不懂可以回去看看条件 int idx = 0; //找到curNode在其父亲节点中的位置 for (int i = 0; i <= parent->keynum; ++i) { if (parent->ptr[i] == curNode) { idx = i; break; } } Node * lsilb = NULL; Node * rsilb = NULL; if (idx - 1 >= 0) {//如果当前结点有左兄弟 lsilb = parent->ptr[idx - 1]; } if (idx + 1 <= parent->keynum) {//说明当前结点有右兄弟 rsilb = parent->ptr[idx + 1]; } //只要右兄弟存在,而且满足rsilb->keynum > lb,即是删除的调整的情况2 if (rsilb && rsilb->keynum > lb) { this->RotateLeft(parent, idx, curNode, rsilb); break; }//如果右兄弟不满足,而左兄弟满足,同样可以 else if (lsilb && lsilb->keynum > lb) { this->RotateRight(parent, idx, curNode, lsilb); break; }//如果左右兄弟都不满足,那就是情况3了, else { //合并到左兄弟, if (lsilb) this->Merge(parent, idx, lsilb, curNode); else//没有左兄弟,合并到右兄弟 this->Merge(parent, idx + 1, curNode, rsilb); // potentially causing deficiency of parent. curNode = parent; parent = curNode->parent; } } if (curNode->keynum == 0) { // root is empty,此时树为空 head = curNode->ptr[0]; delete curNode; }//endif } void BTree::RotateLeft(Node * parent, int idx, Node * cur, Node * rsilb) { //这个是在右兄弟存在的情况下,而且满足rsilb->keynum > lb,则我们需要从把 //右兄弟结点中的最小关键字移动到父亲结点,而父亲结点中小于该右兄弟的关键字的关键字 //就要下移到刚刚删除的那个结点中。 //父亲结点中某个结点下移 cur->key[cur->keynum + 1] = parent->key[idx + 1]; cur->ptr[cur->keynum + 1] = rsilb->ptr[0]; // if (cur->ptr[cur->keynum + 1]) { cur->ptr[cur->keynum + 1]->parent = cur; } rsilb->ptr[0] = NULL; ++cur->keynum; parent->key[idx + 1] = rsilb->key[1]; rsilb->key[idx] = 0; //右兄弟上移一个结点到父亲结点, for (int i = 0; i <= rsilb->keynum; ++i) {//删除最靠右的那个结点 rsilb->key[i] = rsilb->key[i + 1]; rsilb->ptr[i] = rsilb->ptr[i + 1]; } rsilb->key[0] = 0; --rsilb->keynum; } void BTree::RotateRight(Node * parent, int idx, Node * cur, Node * lsilb) { //这个是在左兄弟存在的情况下,而且满足lsilb->keynum > lb,则我们需要从把 //左兄弟结点中的最大关键字移动到父亲结点,而父亲结点中大于该左兄弟的关键字的关键字 //就要下移到刚刚删除的那个结点中。 //因为是在左边插入 for (int i = cur->keynum; i >= 0; --i) {//因为左边的都比右边小,所以要插入第一个位置 cur->key[i + 1] = cur->key[i]; cur->ptr[i + 1] = cur->ptr[i]; } //在第一个位置插入父亲结点下移下来的结点 cur->key[1] = parent->key[idx]; cur->ptr[0] = lsilb->ptr[lsilb->keynum]; if (cur->ptr[0]) cur->ptr[0]->parent = cur; lsilb->ptr[lsilb->keynum] = NULL; ++cur->keynum; // from lsilb to parent. parent->key[idx] = lsilb->key[lsilb->keynum]; lsilb->key[lsilb->keynum] = 0; --lsilb->keynum; } void BTree::Merge(Node * parent, int idx, Node * lsilb, Node * cur) { //函数实现都是往lsilb上合并,首先是先把cur中的剩余部分,全部合到左兄弟中个, for (int i = 0; i <= cur->keynum; ++i) { lsilb->key[lsilb->keynum + 1 + i] = cur->key[i]; lsilb->ptr[lsilb->keynum + 1 + i] = cur->ptr[i]; if (lsilb->ptr[lsilb->keynum + 1 + i]) lsilb->ptr[lsilb->keynum + 1 + i] = lsilb; } //然后再把父亲结点中的idx对应的内容添加到左兄弟 lsilb->key[lsilb->keynum + 1] = parent->key[idx]; lsilb->keynum = lsilb->keynum + cur->keynum + 1; delete cur; //然后更新我们的父亲结点内容 for (int i = idx; i <= parent->keynum; ++i) { parent->key[i] = parent->key[i + 1]; parent->ptr[i] = parent->ptr[i + 1]; }//end for. --parent->keynum; } void BTree::Destroy(Node * & T) { //是否空间 if (!T) { return; } for (int i = 0; i <= T->keynum; ++i) Destroy(T->ptr[i]); delete T; T = NULL; return; } void BTree::WalkThrough(Node * &T) { if (!T) return; static int depth = 0; ++depth; int index = 0; bool running = true; while (running) { int ans = 0; if (index == 0) { ans = 2; } else { cout << "Cur depth: " << depth << endl; cout << "Cur Pos: " << (void*)T << "; " << "Keynum: " << T->keynum << "; " << endl; cout << "Index: " << index << "; Key: " << T->key[index] << endl; do { cout << "1.Prev Key; 2.Next Key; 3.Deepen Left; 4.Deepen Right; 5.Backup << endl; cin >> ans; if (1 <= ans && ans <= 5) break; } while (true); } switch (ans) { case 1: if (index == 1) cout << "Failed." << endl; else --index; break; case 2: if (index == T->keynum) cout << "Failed" << endl; else ++index; break; case 4: if (index > 0 && T->ptr[index]) WalkThrough(T->ptr[index]); else cout << "Failed" << endl; break; case 3: if (index > 0 && T->ptr[index - 1]) WalkThrough(T->ptr[index - 1]); else cout << "Failed" << endl; break; case 5: running = false; break; }//endsw }//endw --depth; } Node * BTree::gethead() { return this->head; }
main.cpp
#include"BTree.h" #define BMT_TEST #ifdef BMT_TEST //BMT: 10 45 24 53 90 3 37 50 61 70 100 int main(void) { BTree t; int n; cout << "输入数的个数:" << endl; cin >> n; cout << "输入各个数的值:" << endl; for (int i = 0; i < n; i++) { int temp; cin >> temp; t.insert_BTree(temp); } Node * head = t.gethead(); t.WalkThrough(head); int key; cout << "输入需要删除的值:" << endl; cin >> key; t.Delete_BTree(key); head = t.gethead(); t.WalkThrough(head); return 0; } #endif

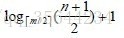

 浙公网安备 33010602011771号
浙公网安备 33010602011771号