数据结构与算法(堆实现优先级队列)

摘录：https://www.cnblogs.com/sfencs-hcy/p/10346607.html

 

优先级队列

如果我们给每个元素都分配一个数字来标记其优先级，不妨设较小的数字具有较高的优先级，这样我们就可以在一个集合中访问优先级最高的元素并对其进行查找和删除操作了。这样，我们就引入了优先级队列 这种数据结构

最简单的优先级队列可能就是一堆不同大小的数组成的队列，每次需要取出其中最小或最大的数，这是我们可以把这些数本身的大小叫做他们的优先级。

实现的想法

最简单的想法是：我们用一个元组来表示元素和它的优先级，将所有的元组都放到列表中存储，接下来当想要找到其中优先级最小的元组时会有以下两种方式

• 1.列表中存储的是乱序的，每次想找最小的时候就遍历一遍找到优先级最小的元组取出。这样操作的时间复杂度其实是O(n)

• 2.列表中的元素已经按照优先级的顺序排好了序，每次取最小的元素时直接找固定位置，但是每次向该优先级队列插入元素时都要进行一次排序将其放入合适的位置，在最坏情况下，时间复杂度同样为O(n)

上面这两种方式的时间复杂度还是较高的，为此，我们使用一种叫做堆的结构来实现优先级队列。

堆

堆其实是一颗二叉树，但它是一种特殊的二叉树，堆中的每个父节点都是要大于等于或者小于等于它的孩子节点。这里是选择大于等于还是小于等于是自己定义，但树中的所以节点都满足一条同样的规则。

在使用堆时，一般我们会想让堆的高度尽可能的小，为此它必须是一颗完全二叉树，这时就会产生一个结论：

堆中有n个元素，那么它的高度h=[log(n)]

我们证明一下这个结论：

完全二叉树0~h-1层的节点数目为2^h-1，在第h层，节点数目最少为1，最多为2^h

于是，n>=2^h-1+1且n<=2^h-1+2^h

分别两边取对数，得出h<=log(n)和h>=log(n+1)-1

由于h是整数，所以h=[log(n)]

用堆实现优先级队列

插入元素

插入元素包括向堆中添加一个元素和堆向上冒泡

添加元素时要为了满足 完全二叉树的特性，需要将其放到树最下层的最右节点的最右位置，如果最下层已经满了，则放到再下一层的最左位置。

堆向上冒泡是一个很有趣的算法，为了使添加元素后的树满足堆排序，需要做一定的调整，调整方法为将添加的元素的优先级与其父节点相比较，如果小于父节点，则该元素与父节点交换，然后再与新的父节点比较，知道父节点小于了自己的优先级或者自己成为了根节点。如图：

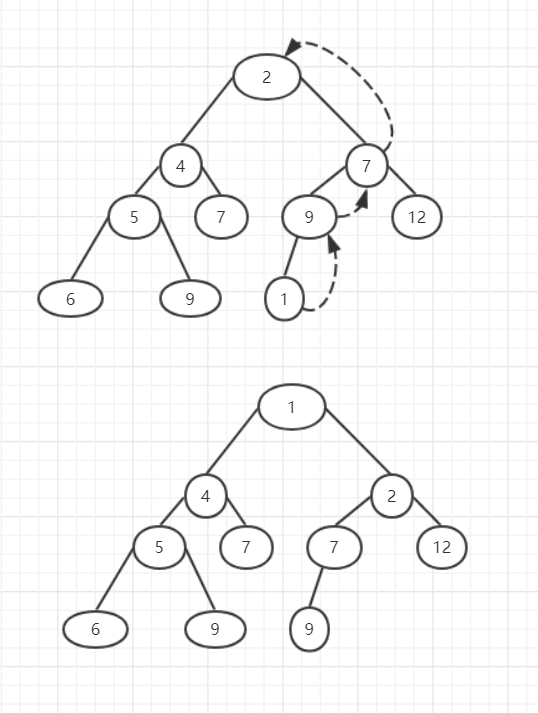
上面的树调整了之后变成了下面的树

移除最小元素

移除最小元素，按理说最小元素就是二叉树的根节点，但是将根节点删除之后，就变成了两颗分离的树，为了保持二叉树的完整性，我们要进行如下操作

首先将根节点与最下层的最右端的节点交换，然后删除这最下层最右端的节点，然后再进行堆的向下排序

堆的向下排序即为将根节点与两个孩子中最小的比较，如果该节点比孩子节点大，则与孩子节点交换，然后继续向下进行直到该节点比两个孩子节点都小或者该节点已经没有孩子了为止。如图：

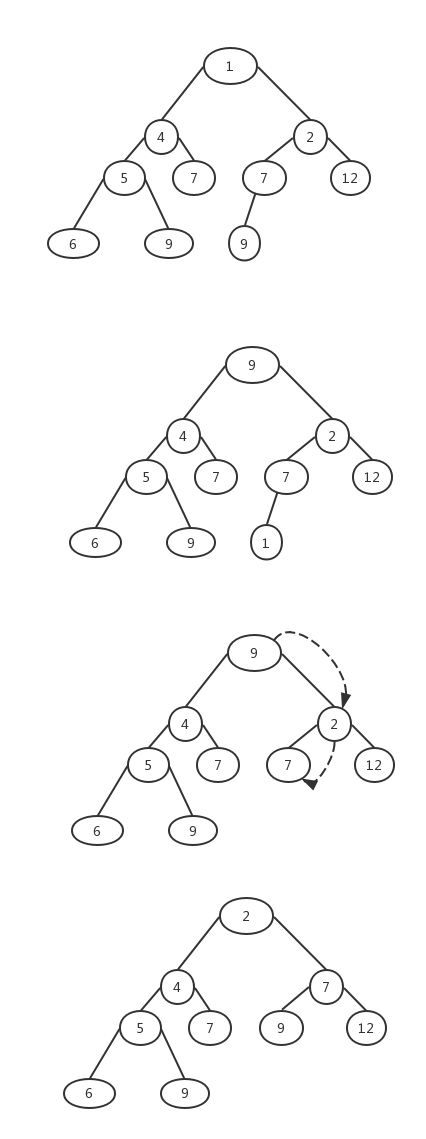
堆的插入与移除元素的复杂度都是log(n)

python实现

对于二叉树的实现，这次我们不使用链式结构，因为堆的排序中，需要定位最下层最右端的这个节点，链式实现起来较为复杂，同时堆是完全二叉树，所以使用基于列表的方式会使问题方便很多

先介绍一下这种实现方式：

列表的首个元素即为二叉树的根节点，所以根节点的索引为1

设节点p的索引函数为f(p)

如果p是位置q的左孩子，则f(p) = 2f(q)+1

如果p是位置q的右孩子，则f(p) = 2f(q)+2

列表中的最后一个元素就是二叉树的最下层的最右端的元素

下面是具体代码：

class Empty(Exception):
    pass

class HeapPriorityQueue():

    """
    使用堆与列表实现的优先级队列
    """

    class Item():
        """
        队列中的项类
        """

        def __init__(self, key, value):
            self.key = key
            self.value = value

        def __it__(self, other):
            return self.key < other.key

    def is_empty(self):
        return len(self) == 0

    def parent(self, j):
        """
        返回父节点的索引
        """
        return (j - 1) // 2

    def left(self, j):
        """返回左孩子索引"""
        return 2 * j + 1

    def right(self, j):
        """返回右孩子索引"""
        return 2 * j + 2

    def has_left(self, j):
        """通过判断索引是否出了列表来判断是否存在"""
        return self.left(j) < len(self.data)

    def has_right(self, j):
        return self.right(j) < len(self.data)

    def swap(self, i, j):
        self.data[i], self.data[j] = self.data[j], self.data[i]

    def upheap(self, j):
        """向上堆排序"""
        parent = self.parent(j)
        if j > 0 and self.data[j] < self.data[parent]:
            self.swap(j, parent)
            self.upheap(parent)

    def downheap(self, j):
        """向下堆排序"""
        if self.has_left(j):
            left = self.left(j)
            small = left
            if self.has_right(j):
                right = self.right(j)
                if self.data[right] < self.data[left]:
                    small = right
            if self.data[small] < self.data[j]:
                self.swap(small, j)
                self.downheap(small)

    def __init__(self):
        self.data = []

    def __len__(self):
        return len(self.data)

    def add(self, key, value):
        """添加一个元素，并进行向上堆排序"""
        self.data.append(self.Item(key, value))
        self.upheap(len(self.data) - 1)

    def min(self):
        if self.is_empty():
            raise Empty('Priority queue is empty')
        item = self.data[0]
        return (item.key, item.value)

    def remove_min(self):
        if self.is_empty():
            raise Empty('Priority queue is empty')
        self.swap(0, len(self.data) - 1)
        item = self.data.pop()
        self.downheap(0)
        return (item.key, item.value)

python的heapq模块

Python标准包含了heapq模块，但他并不是一个独立的数据结构，而是提供了一些函数，这些函数吧列表当做堆进行管理,而且元素的优先级就是列表中的元素本身,除此之外它的模型与实现方式与刚才我们自己定义的基本相同

有以下函数：

• heappush(L,e): 将元素e存入列表L中并进行堆排序

• heappop(L): 取出并返回优先级最小的元素，并重新堆排序

• heappushpop(L,e): 将e放入列表中，同时返回最小元素，相当于先执行push，再pop

• heap replace(L,e): 与heappushpop类似，是先执行pop，再执行push

• heapify(L): 将未堆排序的列表进行调整使之满足堆的结构。采用了自底向上的堆构造算法，时间复杂度为O(n)

• 等等