数据结构与算法(排序算法)

一、冒泡排序

　　

　　冒泡排序原理：

• • 1.将原始列表中的最大值找出且放置在列表最右侧(将元素两两比较，将数值大的数逐步向后移动)
  • 2.重复执行步骤1

　　代码步骤：

　　第一步：

#将原始列表中的最大值找出且放置在列表最右侧(将元素两两比较，将数值大的数逐步向后移动)
def sort(alist):
    for i in range(len(alist)-1):
        if alist[i] > alist[i+1]:
            alist[i],alist[i+1] = alist[i+1],alist[i]
    return alist

　　第二步：

# 冒泡排序
def sort(alist):
    # 循环列表长度次数
    for j in range(len(alist) - 1):
        # 循环 比较前一个元素与后一个元素的大小
        for i in range(len(alist) - 1 - j):
            # 判断前一个元素比后一个元素大，元素交换位置
            if alist[i] > alist[i + 1]:
                # 元素交换位置
                alist[i],alist[i + 1] = alist[i + 1],alist[i]
                
    # 返回列表元素
    return alist

　　测试结果：

alist = [3,6,1,4,8,2]
print(sort(alist))
#结果：>>>[1, 2, 3, 4, 6, 8]

二、选择排序

　　选择排序改进了冒泡排序，每次遍历列表只做一次交换。为了做到这一点，一个选择排序在他遍历时寻找最大的值，并在完成遍历后，将其放置在正确的位置。

　　对于冒泡排序来讲选择排序由于交换数量的减少，选择排序通常在基准研究中执行得更快。

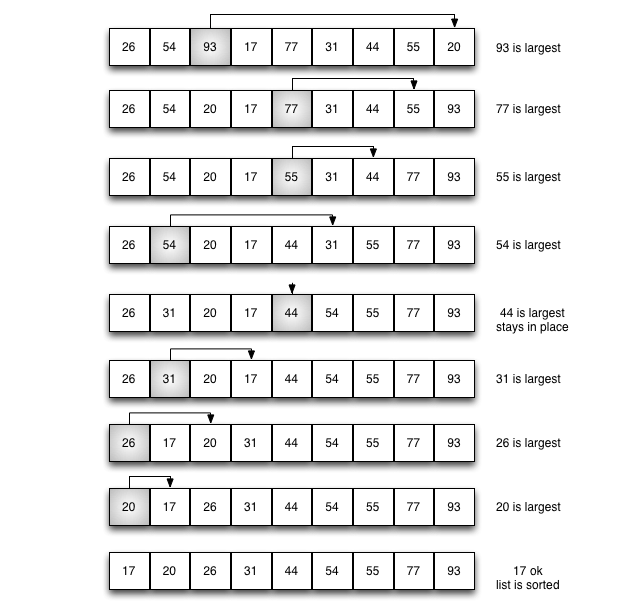
　　排序原理：

　　将列表中的最大值一次找出，放置在列表最右侧

　　代码步骤：

　　第一步：

#将列表中的最大值的下标找到
def sort(alist):
    max_index = 0 #最大值的下标
    for i in range(1,len(alist)):
        if alist[max_index] < alist[i]:
            max_index = i
    print(max_index)

　　第二步：

#将列表中的最大值一次找出，放置在列表最右侧
def sort(alist):
    max_index = 0 #最大值的下标
    for i in range(1,len(alist)):
        if alist[max_index] < alist[i]:
            max_index = i
    alist[max_index],alist[len(alist)-1] = alist[len(alist)-1],alist[max_index]
    
    return alist

　　第三步：

def sort(alist):
    # 循环次数为列表长度-1，且是反向循环
    for j in range(len(alist),1,-1):
        # 最大值的下标
        max_index = 0
        # 每次循环，找出最大值放在列表最右端，找寻下一个值时，不再需要判断最后一个值大小(最大)
        for i in range(1,j):
            # 判断前后相邻元素的比较，从第一个元素开始比较
            if alist[max_index] < alist[i]:
                # 当条件不满足时，max_index索引被赋值下一个元素i,i则+1 继续下一轮循环比较
                max_index = i
        # 每次循环一次j，则找到最大元素下标max_index,通过元素下标与列表最后一个元素交换位置
        alist[max_index],alist[j-1] = alist[j-1],alist[max_index]
        
    # 返回alist
    return alist

　　测试结果：

alist = [3,6,1,4,8,2]
sort(alist)
#结果>>>[1, 2, 3, 4, 6, 8]

三、插入排序

　　插入排序的主要思想是每次取一个列表元素与列表中已经排序好的列表段进行比较，然后插入从而得到新的排序好的列表段，最终获得排序好的列表。比如，待排序列表为[49,38,65,97,76,13,27,49]，则比较的步骤和得到的新列表如下：(带有背景颜色的列表段是已经排序好的，红色背景标记的是执行插入并且进行过交换的元素）

　　

　　排序原理：

　　将乱序列表分成两部分，一部分是有序部分，一部分是乱序部分，将乱序部分的每一个元素插入到有序部分的合适位置

　　[5,   3,9,4,1]

　　[3,5,   9,4,1]

　　[3,5, 9,  4,1] 

　　[3,4,5,9,   1]

　　[3,4,5,9, 1]

　　代码步骤：

　　第一步：

#执行第一次插入操作
def sort(alist):
    i = 1
    # alist[i-1]:第一次插入时的有序列表
    # alist[i]:乱序列表中的第一个列表元素
    if alist[i] < alist[i-1]:
        alist[i],alist[i-1] = alist[i-1],alist[i] 

　　第二步：

def sort(alist):
    i = 2
    # alist[i-1]:第一次插入时的有序列表
    # alist[i]:乱序列表中的第一个列表元素
    if alist[i] < alist[i-1]:
        alist[i],alist[i-1] = alist[i-1],alist[i] 

　　第三步：

def sort(alist):
    i = 3
    # alist[i-1]:第一次插入时的有序列表
    # alist[i]:乱序列表中的第一个列表元素
    while i > 0:
        if alist[i] < alist[i-1]:
            alist[i],alist[i-1] = alist[i-1],alist[i] 
            i -= 1
        else:
            break

　　第四步：

# alist[i-1]:第一次插入时的有序列表
# alist[i]:乱序列表中的第一个列表元素
def sort(alist):
    # 循环列表长度
    for i in range(1,len(alist)):
        
        # 当前元素比有序列表中的所有元素小，插入第一个位置，i-1<0条件不成立，结束wehile循环
        while i > 0:
            # 判断后一个元素小于前一个元素时，元素交换位置
            if alist[i] < alist[i - 1]:
                # 前后元素位置交换
                alist[i],alist[i-1] = alist[i-1],alist[i]
                # 继续比较与有序列表中的前一个位置元素大小，直到小于前一个位置元素
                i -= 1
            else:
                # 当前元素大于有序列表中最后一个元素时，当前元素位置不动(当前元素大于有序列表中最大值)
                break
                
    # 返回列表
    return alist

　　测试结果：

alist = [49,38,65,97,76,13,27]
print(sort(alist))
#结果>>>[13, 27, 38, 49, 65, 76, 97]

四、希尔排序

　　希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量（gap）”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高。

　　

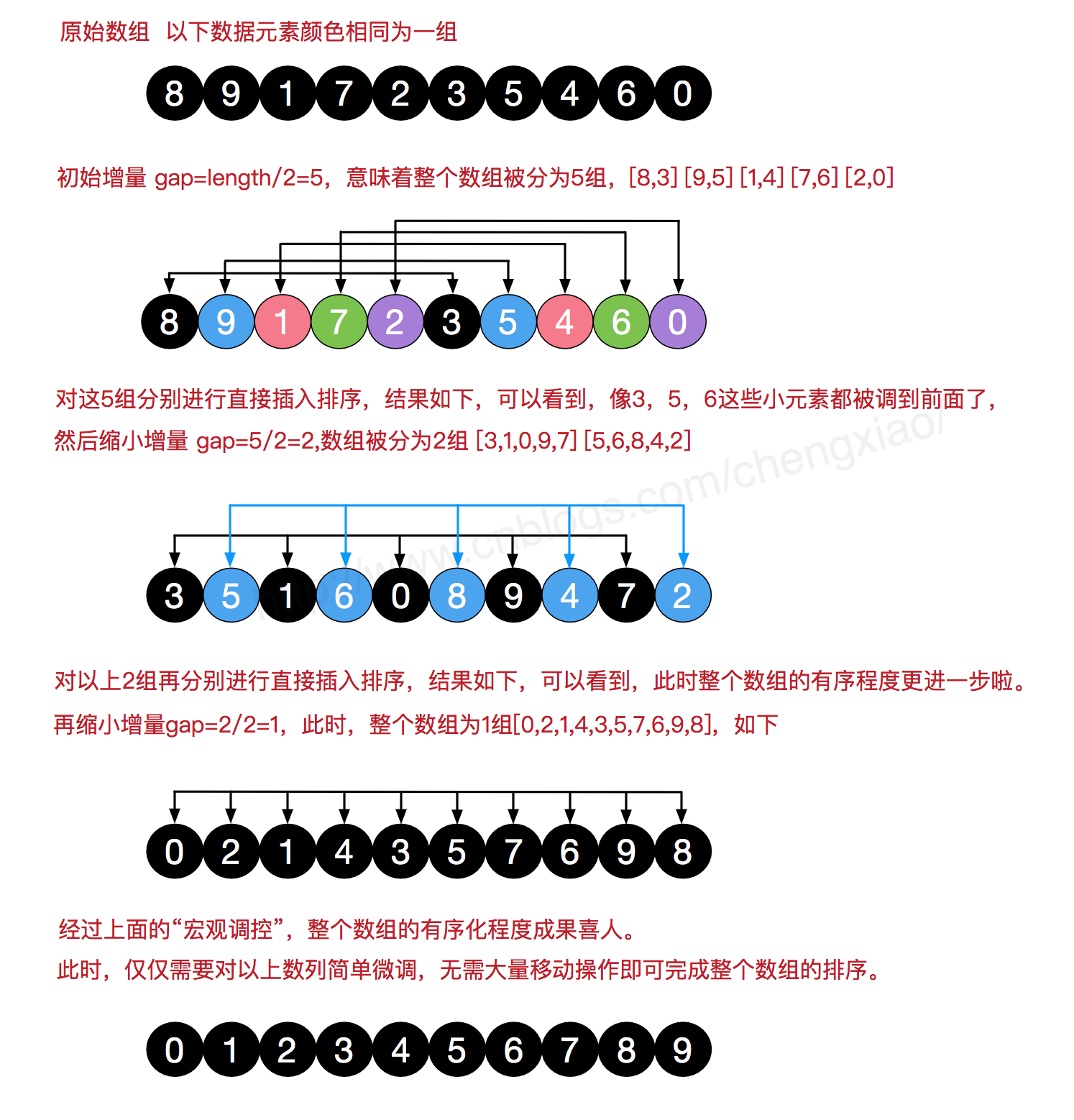
　　排序原理：

　　增量为1的希尔排序就是插入排序

　　代码步骤：

　　第一步：

#增量为1的希尔排序（插入排序的核心）
def sort(alist):
    #增量
    gap = len(alist) // 2
    
    for i in range(1,len(alist)):
        # alist[i-1]:第一次插入时的有序列表
        # alist[i]:乱序列表中的第一个列表元素
        while i > 0:
            if alist[i] < alist[i-1]:
                alist[i],alist[i-1] = alist[i-1],alist[i] 
                i -= 1
            else:
                break
    return alist

　　第二步：

#增量为gap的希尔排序
def sort(alist):
    #增量
    gap = len(alist) // 2
    for i in range(gap,len(alist)):
        # alist[i-1]:第一次插入时的有序列表
        # alist[i]:乱序列表中的第一个列表元素
        while i > 0:
            if alist[i] < alist[i-gap]:
                alist[i],alist[i-gap] = alist[i-gap],alist[i] 
                i -= gap
            else:
                break
    return alist

　　第三步：

# 继续缩小增量（gap）
def sort(alist):
    # 增量 每次增量的索引值是列表元素长度的一半
    gap = len(alist) // 2
    
    # 增量值条件为1时，排序完成
    while gap >= 1 :
        
        # 循环列表长度
        for i in range(gap,len(alist)):
            
            # alist[i-1]:第一次插入时的有序列表
            # alist[i]:乱序列表中的第一个列表元素
            while i > 0:
                if alist[i] < alist[i-gap]:
                    alist[i],alist[i-gap] = alist[i-gap],alist[i] 
                    i -= gap
                else:
                    break
                    
        # 增量值取一半
        gap //= 2
    return alist

　　测试代码：

alist = [49,38,65,97,76,13,27]
print(sort(alist))
# 结果：>>>[13, 27, 38, 49, 65, 76, 97]

五、快速排序

• 将列表中第一个元素设定为基准数字，赋值给mid变量，然后将整个列表中比基准小的数值放在基准的左侧，比基准到的数字放在基准右侧。然后将基准数字左右两侧的序列在根据此方法进行排放。
• 定义两个指针，low指向最左侧，high指向最右侧(先移动右侧high指针)
• 然后对最右侧指针进行向左移动，移动法则是，如果指针指向的数值比基准小，则将指针指向的数字移动到基准数字原始的位置，否则继续移动指针。
• 如果最右侧指针指向的数值移动到基准位置时，开始移动最左侧指针，将其向右移动，如果该指针指向的数值大于基准则将该数值移动到最右侧指针指向的位置，然后停止移动。
• 如果左右侧指针重复则，将基准放入左右指针重复的位置，则基准左侧为比其小的数值，右侧为比其大的数值。

　　排序原理：

　　将将比基准小的排列在基准左侧，比基准大的排列在基准右侧

　　代码步骤：

　　第一步：

def sort(alist):
    low = 0
    high = len(alist)-1
    #基准：最左侧的数值
    mid = alist[low]
    #low和high的关系只能是小于，当等于的时候就要填充mid了
    while low < high:
        while low < high:
            if alist[high] > mid:
                high -= 1
            else:
                alist[low] = alist[high]
                break
        while low < high:
            if alist[low] < mid:
                low += 1
            else:
                alist[high] = alist[low]
                break
        
        #当low和high重复的时候，将mid填充
        if low == high:
            alist[low] = mid #or alist[high] = mid  
            break
    return alist
    

　　第二步：

def sort(alist,start,end):
    low = start
    high = end
    
    # 当索引最小值大于最大值，退出递归
    if low > high:
        return 
    
    # 定义列表第一个索引下标为mid值
    mid = alist[low]
    
    
    while low < high:
        # 先从列表的最右边，high开始判断
        while low < high:
            # high指向的值大于中间值则元素位置不改变，high-1
            if alist[high] > mid:
                high -= 1
            else:
                # 条件不满足时，交换中间值mid(当前mid为索引0位置的值)
                alist[low] = alist[high]
                break
             
        # high指针移动后，在移动low指针
        while low < high:
            if alist[low] < mid:
                low += 1
            else:
                # 找到low指针指向的值大于mid中间值时，把当前low的值放入之前high指针对应位置
                alist[high] = alist[low]
                break
            
    # 当前循环到low指针与high指针重合时，条件不成立，退出循环(low=high)
    alist[low] = mid  # 同alist[high] = mid
    
    # 递归
    sort(alist,start,high-1)
    sort(alist,low+1,end) #将基准右侧的子列表进行递归操作
    
    # 返回最后排序的列表值
    return alist
    

　　测试结果:

alist = [2,4,5,1,3]
print(sort(alist,0,len(alist)-1))
#结果>>>[1, 2, 3, 4, 5]

六、归并排序

　　归并排序采用分而治之的原理：

　　　　- 将一个序列从中间位置分成两个序列；

　　　　- 在将这两个子序列按照第一步继续二分下去；

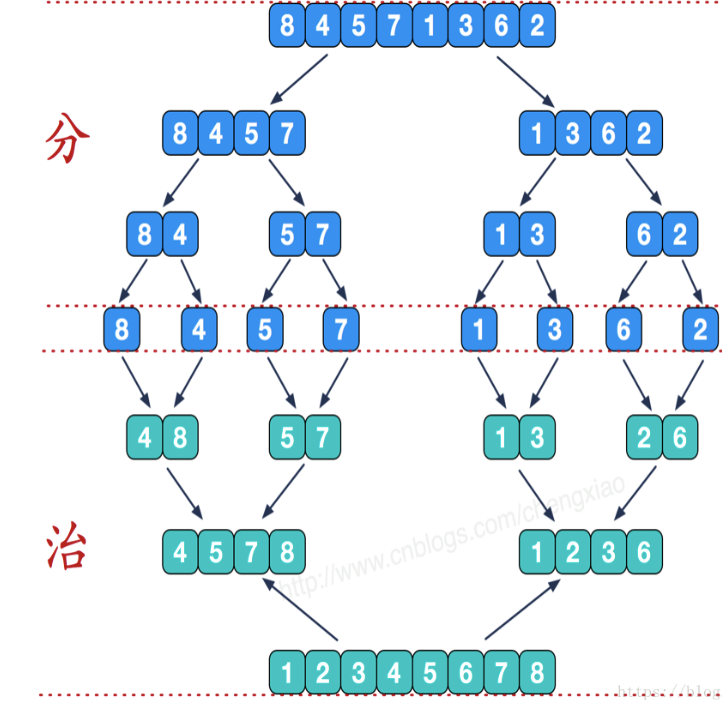
　　　　- 直到所有子序列的长度都为1，也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。

　　如何合并：

　　下图中的倒数第三行表示为第一次合并后的数据。其中一组数据为 4 8  ，  5 7。该两组数据合并方式为：每一小组数据中指定一个指针，指针指向每小组数据的第一个元素，通过指针的偏移指定数据进行有序排列。排列情况如下：

　　　　1. p1指向4，p2指向5，p1和p2指向的元素4和5进行比较，较小的数据归并到一个新的列表中。经过比较p1指向的4会被添加到新的列表中，则p1向后偏移一位，指向了8，p2不变。

　　　　2.p1和p2指向的元素8，5继续比较，则p2指向的5较小，添加到新列表中，p2向后偏移一位，指向了7。

　　　　3.p1和p2指向的元素8，7继续比较，7添加到新列表中，p2偏移指向NULL，比较结束。

　　　　4.最后剩下的指针指向的数据（包含该指针指向数据后面所有的数据）直接添加到新列表中即可。

　　

 

def merge_sort(alist):
    n = len(alist)
    #结束递归的条件
    if n <= 1:
        return alist
    #中间索引
    mid = n//2

    left_li = merge_sort(alist[:mid])
    right_li = merge_sort(alist[mid:])

    #指向左右表中第一个元素的指针
    left_pointer,right_pointer = 0,0
    #合并数据对应的列表：该表中存储的为排序后的数据
    result = []
    while left_pointer < len(left_li) and right_pointer < len(right_li):
        #比较最小集合中的元素，将最小元素添加到result列表中
        if left_li[left_pointer] < right_li[right_pointer]:
            result.append(left_li[left_pointer])
            left_pointer += 1
        else:
            result.append(right_li[right_pointer])
            right_pointer += 1
    #当左右表的某一个表的指针偏移到末尾的时候，比较大小结束，将另一张表中的数据（有序）添加到result中
    result += left_li[left_pointer:]
    result += right_li[right_pointer:]

    return result

alist = [3,8,5,7,6]
print(merge_sort(alist))