数据结构与算法(二叉树结构)
一、二叉树
1.1 二叉树的定义:
二叉树是一种特殊的树,它具有以下特点:
(1)树中每个节点最多只能有两棵树,即每个节点的度最多为2。
(2)二叉树的子树有左右之分,即左子树与右子树,次序不能颠倒。
(3)二叉树即使只有一个子树时,也要区分是左子树还是右子树。
1.2 满二叉树:
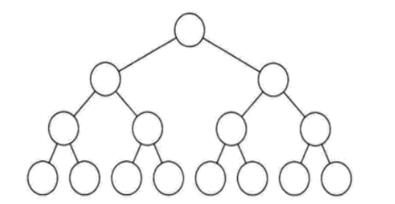
满二叉树作为一种特殊的二叉树,它是指:所有的分支节点都存在左子树与右子树,并且所有的叶子节点都在同一层上。其特点有:
(1)叶子节点只能出现在最下面一层
(2)非叶子节点度一定是2
(3)在同样深度的二叉树中,满二叉树的节点个数最多,节点个数为: 2h−12h−1 ,其中 hh 为树的深度。
1.3 完全二叉树:
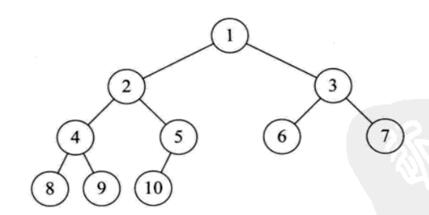
若设二叉树的深度为 hh ,除第 hh 层外,其它各层 (1~h−1)(1~h−1) 的结点数都达到最大个数,第 hh 层所有的结点都连续集中在最左边,这就是完全二叉树。其具有以下特点:
(1)叶子节点可以出现在最后一层或倒数第二层。
(2)最后一层的叶子节点一定集中在左部连续位置。
(3)完全二叉树严格按层序编号。(可利用数组或列表进行实现,满二叉树同)
(4)若一个节点为叶子节点,那么编号比其大的节点均为叶子节点。
二、二叉树的相关性质
2.1 二叉树性质:
(1)在非空二叉树的 ii 层上,至多有 2i−12i−1 个节点 (i≥1)(i≥1) 。
(2)在深度为 hh 的二叉树上最多有 2h−12h−1 个节点 (k≥1)(k≥1) 。
(3)对于任何一棵非空的二叉树,如果叶节点个数为 n0n0 ,度数为 22 的节点个数为 n2n2 ,则有: n0=n2+1n0=n2+1 。
2.2 完全二叉树性质:
(1)具有 nn 个的结点的完全二叉树的深度为 log2n+1log2n+1 。.
(2)如果有一颗有 nn 个节点的完全二叉树的节点按层次序编号,对任一层的节点 i,(1≥i≥n)i,(1≥i≥n) 有:
(2.1)如果 i=1i=1 ,则节点是二叉树的根,无双亲,如果 i>1i>1 ,则其双亲节点为 ⌊i/2⌋⌊i/2⌋ 。
(2.2)如果 2i>n2i>n 那么节点i没有左孩子,否则其左孩子为 2i2i 。
(2.3)如果 2i+1>n2i+1>n 那么节点没有右孩子,否则右孩子为 2i+12i+1 。
三、二叉树的数据结构(排序方式)
想要遍历一棵二叉树,有两种不同的策略:深度优先遍历和宽度(广度)优先遍历。
其中深度优先遍历策略有三种不同的方式:
前序遍历:按根节点、左子树、右子树的顺序遍历。
中序遍历:按左子树、根节点、右子树的顺序遍历。
后序遍历:按左子树、右子树、根节点的顺序遍历。
四、python实现二叉树
# 创建二叉树节点 class Node(object): def __init__(self,item): self.item = item self.left = None self.right = None # 创建二叉树 class Tree(object): # 构建一颗空二叉树 def __init__(self): # 指针指向根节点,当前树为空,指向None self.root = None # 添加子节点 def addNode(self,item): node = Node(item) cur = self.root # 判断如果新节点是根节点 if self.root == None: self.root = node return # 如果树不为空情况,需要通过队列循环来遍历节点是否为空 # 先将根节点指针放入列表,作为遍历起始点 q = [cur] while q: # 删除队列中最左侧元素 n = q.pop(0) # 判断左节点是否为空 if n.left == None: n.left = node break else: q.append(n.left) # 判断右节点是否为空 if n.right == None: n.right = node break else: q.append(n.right) # 树的广度遍历 def travel(self): cur = self.root q = [cur] while q: # 删除列表中最左侧(最先进入的子节点)元素 n = q.pop(0) print(n.item) # 当前节点的左子节点不为None,说明子节点存在,追加子节点地址到列表 if n.left != None: q.append(n.left) # 当前节点的右子节点不为None,说明子节点存在,追加子节点地址到列表 if n.right != None: q.append(n.right) # 树的深度遍历(前序遍历,中序遍历,后序遍历) # 前序遍历(根左右) def frontTravel(self,root): # 判断当子节点为空时,结束递归 if root == None: return # 获取节点的值 print(root.item) # 通过递归获取根左节点地址 self.frontTravel(root.left) # 通过递归获取根右节点地址 self.frontTravel(root.right) # 中序遍历(左根右) def midTravel(self,root): # 判断当子节点为空时,结束递归 if root == None: return # 通过递归获取根左节点地址 self.midTravel(root.left) # 获取节点的值 print(root.item) # 通过递归获取根右节点地址 self.midTravel(root.right) # 后序遍历(左右根) def afterTravel(self,root): # 判断当子节点为空时,结束递归 if root == None: return # 通过递归获取根左节点地址 self.afterTravel(root.left) # 通过递归获取根右节点地址 self.afterTravel(root.right) # 获取节点的值 print(root.item)
测试:
# 测试 tree = Tree() tree.addNode(1) tree.addNode(2) tree.addNode(3) tree.addNode(4) tree.addNode(5) tree.addNode(6) # 广度遍历树 # tree.travel() # 深度遍历树 # tree.frontTravel(tree.root) # 1 2 4 5 3 6 # tree.midTravel(tree.root) # 4 2 5 1 6 3 tree.afterTravel(tree.root) # 4 5 2 6 3 1
五、排序二叉树
插入节点的准则:首先插入根节点。当插入其他节点的时候,需要和根节点做比较,比根节点小的节点插入树的左侧,大的插入树的右侧
class Node(): def __init__(self,item): self.item = item self.left = None self.right = None class SortTree(): def __init__(self): self.root = None def midTravel(self,root): if root == None: return #左根右 self.midTravel(root.left) print(root.item) self.midTravel(root.right) def insertNode(self,item): node = Node(item) cur = self.root #树为空 if self.root == None: self.root = node return #树为非空 while True: if cur.item > node.item: if cur.left == None: cur.left = node break else: cur = cur.left else: if cur.right == None: cur.right = node break else: cur = cur.right
测试:
t = SortTree() t.insertNode(3) t.insertNode(8) t.insertNode(3) t.insertNode(1) t.insertNode(1) t.midTravel(t.root) #结果:>>> 1 1 3 3 8


