数据结构与算法(基本数据结构-顺序表与链表)

一、理解计算机内存

　　计算机的作用：对数据进行存储和运算。首先我们需要知道我们目前使用的计算机都是二进制的计算机，就以为着计算机只可以存储和运算二进制的数据。例如下载好的一部电影，该电影可以存储到计算机中，计算机中存储的是基于二进制的电影数据，然后我们可以通过相关的视频播放软件结合相关的硬件对电影的二进制数据进行相关的运算操作，所产生的结果就是我们可以看到电影的画面和听到音频的声音。

　　　- 问题：阐述计算机如何计算1+2的结果？

 　　　- 阐述：简单理解为,首先可以将1和2输入到计算机中，然后计算机会将1和2转换成二进制的数据进行数据存储，然后通过加法器进行两个二进制数值的计算并返回结果。

　　　- 分析：上述的阐述中提到，计算机首先需要存储1和2这两个数值，那么计算机如何进行数据的存储呢？那么毫无疑问，计算机可以将数据直接存储到内存中。

　　　- 变量：我们在编程世界中，可以将某个数值直接赋值给一个变量，但是最终数值会被存储到计算机的内存中，因此我们可以理解为，变量表示的就是计算机中进行数据存储的某一块内存。

　　如何形象化的理解计算机的内存？

　　　- 举例：将计算机的内存空间映射到我们现实生活中的话，内存就好比是我们在现实生活中三维立体的空间。生活在北京的北漂们，几乎都居住的是一个独立的公寓或者合租在一个几居室的某一个房间中，那么北漂甲就好比是数据，而他所居住的房间则就是存储数据的一块内存空间。

　　　- 分析：从上述案例中，我们可以得知北漂甲居住的房间会有两个基本的属性，其一就是房间空间的大小，其二就是房间的一个位置标识（门牌号）。那么计算机中存储数据的内存空间也会有这两个最基本的属性：内存空间大小和内存空间的地址。内存空间的大小可以表示该空间可以存储数据值的大小范围，内存空间的地址（用十六进制数值表示）可以用来通过寻址定位、查找到该内存空间中所存储的数据值。

　　　- 如何理解 a = 10 这条赋值语句对应的内存图呢？

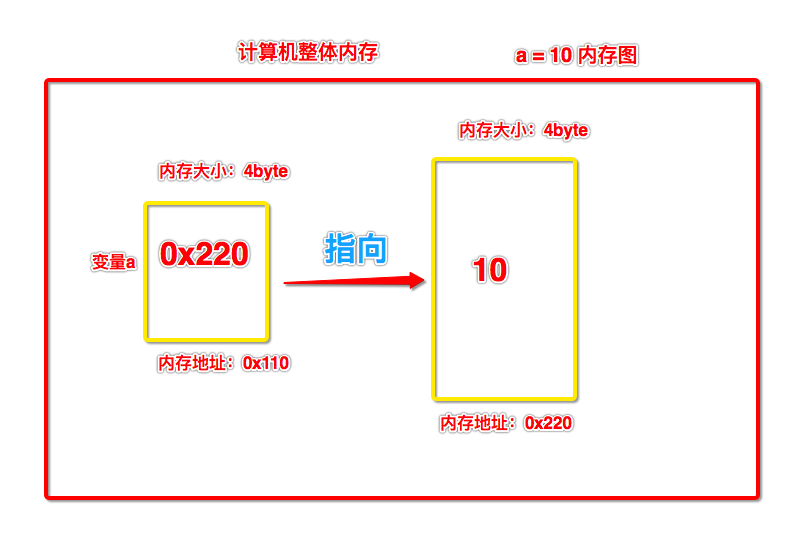
　　- 引用：当一个变量中存储的是某一块内存空间的地址，则该变量即可成为那块内存空间的引用。a=10，a就是10所在内存空间的一个引用。

　　- 指向：当一个变量中存储了一块内存空间的地址，则称该变量（引用）指向了那块内存。

　　- 不同类型数据占用内存空间的大小：整形（4字节），浮点型（8字节），字符型（1字节）

二、顺序表

　　集合中存储的元素是有顺序的。顺序表的结构可以分为两种形式：单数据类型和多数据类型。

　　单数据类型：例如np.array

　　单数据类型：内存连续开辟，在内存中存储 int a = 10，20，30图例如下

　　

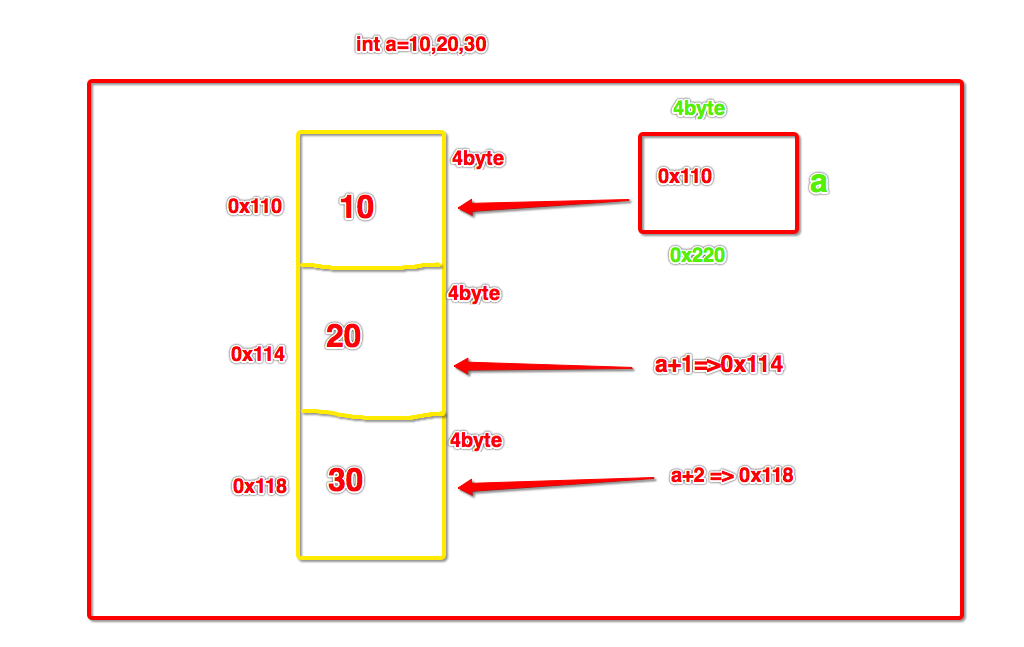
　　多数据类型：例如python中的list

　　多数据类型：内存非连续开辟，在内存中如何存储 li = 10,'a',96.5,如何获取每一个数据值呢？

　　

 　　- 顺序表的弊端：顺序表的结构需要预先知道数据大小来申请连续的存储空间，而在进行增加删除时又需要进行数据的搬迁。

　 　- Python中的 list 和 tuple 两种类型采用了顺序表的实现技术。

三、链表

　　相对于顺序表，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。

　　链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是每一个结点（数据存储单元）里存放下一个结点的信息（即地址）：

　　

四、单向链表：

　　单向链表也叫单链表，是表中最简单的一种形式，它的每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

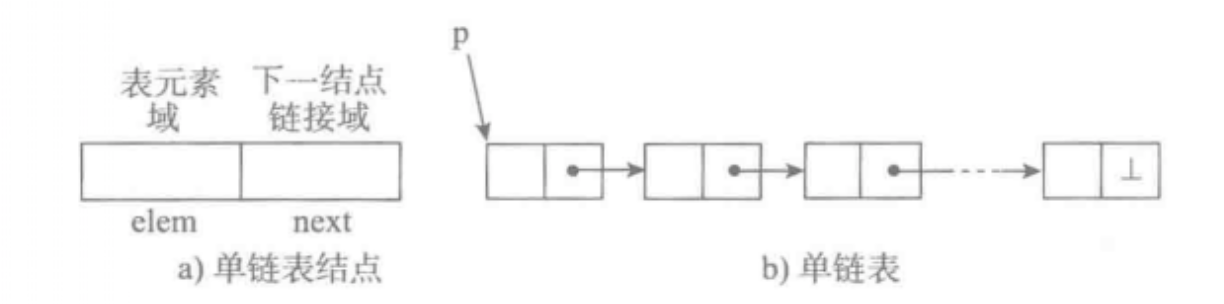
　　　　- 表中元素elem用来存放具体的数据。

　　　　- 链接域next用来存放下一个节点的位置。

　　　　- 变量p指向链表的头节点（首节点）的位置，从p出发能找到表中的任意节点。

　　单向链表的抽象数据类型定义：

　　　　. is_empty()：链表是否为空

　　　　. length()：链表长度

　　　　. travel()：遍历整个链表

　　　　. add(item)：链表头部添加元素

　　　　. append(item)：链表尾部添加元素

　　　　. insert(pos, item)：指定位置添加元素

　　　　. remove(item)：删除节点

　　　　. search(item)：查找节点是否存在

# 第一步：创建节点(node)
class Node(object):
    def __init__(self,item):
        # 存放新节点的值
        self.item = item
        # 新节点没有下一个链接地址
        self.next = None

# 创建链接
class Link(object):
    def __init__(self):
        # _head永远指向的第一个节点的地址
        self._head = None
        
    # 添加一个链接
    def add(self,item):
        # 创建新节点
        node = Node(item)
        # 将新节点的next地址指向 旧节点的_head指向
        node.next = self._head
        # 新节点地址指向新节点内存空间地址
        self._head = node
        
    # 获取链表值
    def travel(self):
        # 获取第一个节点指针
        cur = self._head
        
        # 判断链表next指向为空时，则为链表的最后一个节点
        while cur:
            # 打印节点item属性值
            print(cur.item)
            # 将新的节点指针赋值给cur变量
            cur = cur.next
            
    def length(self):
        # 获取第一个节点指针
        cur = self._head
        # 长度计数器
        count = 0
        
        # 判断链表next指向为空时，则为链表的最后一个节点
        while cur:
            # 打印节点item属性值
            count += 1
            # 将新的节点指针赋值给cur变量
            cur = cur.next
            
        # 打印计数器
        print("当前链表长度： ",count)
        return count
        


    # 判断链表是否为空
    def isEmpty(self):
        # 判断链表指针为None时，链表为空，返回True
        return self._head == None

    
    # 链表尾部追加元素
    def append(self,item):
        node = Node(item)

        # 判断链表是否为空
        if self.isEmpty():
            # 链表为空，添加新节点
            self._head = node
            return

        # 链表不为空，追加节点
        cur = self._head
        # 定义一个变量，保存前一个节点的地址
        pre = None

        # 判断
        while cur:
            pre = cur
            cur = cur.next

        # 最后next指针指向新加节点
        pre.next = node

    # 查询链表 查询成功返回True,否则返回False
    def search(self,item):
        find = False
        cur = self._head

        while cur:
            # 查询成功
            if cur.item == item:
                find = True
                break
            else:
                # 链表指针指向下一个链表节点
                cur = cur.next

        return find

    # 链表的插入操作
    def insert(self,pos,item):
        # 查询链表长度
        length = self.length()
        if pos <=0 or pos >length:
            print("插入位置超出范围！！！")
            return

        # pos添加的位置规定从1开始
        node = Node(item)
        cur = self._head
        pre = None
        
        # 在位置1插入
        if pos == 1:
            node.next = self._head
            self._head = node
            return 

        # for循环，使链表指针指向pos插入位置
        for i in range(1,pos):
            pre = cur
            cur = cur.next

        # 此时链表指针指向需要插入数据的位置
        # 此时把pre指向的上一个指针地址指向插入节点的地址
        pre.next = node
        # 把插入节点地址指针指向下一个节点地址
        node.next = cur

    # 删除指定位置节点
    def remove(self,item):
        # 获取第一个节点指针
        cur = self._head
        pre = None

        # 此处没有节点可以删除
        if self._head == None:
            return

        # 删除第一个节点
        if cur.item == item:
            self._head = cur.next
            return

        # 删除其他位置节点
        while cur:
            # 将新的节点指针赋值给下一个节点地址
            if cur.item == item:
                pre.next = cur.next
                break
            else:
                pre = cur
                cur = cur.next



# 链表测试
# 实例化链表对象
link = Link()
# 添加节点
link.add(1)
link.add(2)
link.add(3)
# 显示链表值
link.travel()

# 删除元素2
link.remove(2)
link.travel()

# 插入在链表位置1处插入一个节点6
link.insert(4,8)
link.travel()

五、单向循环链表

　　单链表的一个变形是单向循环链表，链表中最后一个节点的next域不再为None，而是指向链表的头结点。

　　基本操作和单链表基本一样，实现代码如下：

# coding=utf-8
# 单向循环链表


class Node:
    """节点"""
    def __init__(self, item):
        self.item = item
        self.next = None

    def __str__(self):
        return str(self.item)


class SinCycLinkedList:
    """单向循环链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        if self.is_empty():
            return 0
        count = 1
        cur = self._head
        while cur.next != self._head:
            # print("cur", cur.item)
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历"""
        if self.is_empty():
            return

        cur = self._head
        print(cur.item)
        while cur.next != self._head:
            cur = cur.next
            print(cur.item)

    def add(self, item):
        """在头部添加一个节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            node.next = self._head
            cur = self._head
            while cur.next != self._head:
                cur = cur.next

            cur.next = node
            self._head = node

    def append(self, item):
        """在尾部添加一个节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            cur = self._head
            # print(type(cur), cur.item, cur.next)
            while cur.next != self._head:
                cur = cur.next

            # print(cur.item)
            cur.next = node
            node.next = self._head

    def insert(self, pos, item):
        """指定位置pos添加节点"""
        if pos <= 0:
            self.add(item)
        elif pos > (self.length() - 1):
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            cur_pos = 0
            while cur.next != self._head:
                if (pos - 1) == cur_pos:
                    node.next = cur.next
                    cur.next = node
                    break
                cur_pos += 1
                cur = cur.next

    def remove(self, item):
        """删除一个节点"""
        if self.is_empty():
            return

        pre = self._head
        # 删除首节点
        if pre.item == item:
            cur = pre
            while cur.next != self._head:
                cur = cur.next

            cur.next = pre.next     # 删除首节点（跳过该节点）
            self._head = pre.next   # 重新指定首节点

        # 删除其他的节点
        else:
            cur = pre
            while cur.next != self._head:
                if cur.next.item == item:
                    cur.next = cur.next.next
                cur = cur.next

    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return -1

        cur_pos = 0
        cur = self._head
        if cur.item == item:
            return cur_pos

        while cur.next != self._head:
            if cur.item == item:
                return cur_pos
            cur_pos += 1
            cur = cur.next

        if cur_pos == self.length() - 1:
            return -1


if __name__ == "__main__":
    ll = SinCycLinkedList()
    ll.add(1)       # 1
    ll.add(2)       # 2 1
    # ll.travel()
    ll.append(3)    # 2 1 3
    ll.insert(2, 4) # 2 1 4 3
    ll.insert(4, 5) # 2 1 4 3 5
    ll.insert(0, 6) # 6 2 1 4 3 5
    print("length:", ll.length())        # 6
    ll.travel()                           # 6 2 1 4 3 5
    print("search(3)", ll.search(3))     # 4
    print("search(7)", ll.search(7))     # -1
    print("search(6)", ll.search(6))    # 0
    print("remove(1)")
    ll.remove(1)
    print("length:", ll.length())       # 6 2 4 3 5
    print("remove(6)")
    ll.remove(6)
    ll.travel()

六、双向链表

　　一种更复杂的链表是 "双向链表" 或 "双面链表"。每个节点有两个链接：一个指向前一个节点，当次节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。

　　

　　代码实现：

# coding=utf-8
# 双向链表


class Node:
    """节点"""
    def __init__(self, item):
        self.item = item
        self.prev = None
        self.next = None


class DLinkList:
    """双向链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """获取链表长度"""
        if self.is_empty():
            return 0
        else:
            cur = self._head
            count = 1
            while cur.next is not None:
                count += 1
                cur = cur.next

            return count

    def travel(self):
        """遍历链表"""
        print("↓↓" * 10)
        if self.is_empty():
            print("")

        else:
            cur = self._head
            print(cur.item)
            while cur.next is not None:
                cur = cur.next
                print(cur.item)
        print("↑↑" * 10)

    def add(self, item):
        """链表头部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head

            node.next = cur
            cur.prev = node
            self._head = node

    def append(self, item):
        """链表尾部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            # 遍历找到最后一个节点
            while cur.next is not None:
                cur = cur.next

            # 在尾节点添加新的节点
            cur.next = node
            node.prev = cur

    def insert(self, pos, item):
        """指定位置添加"""
        # 头部添加
        if pos <= 0:
            self.add(item)

        # 尾部添加
        elif pos > (self.length() - 1):
            self.append(item)

        # 其他位置添加
        else:
            node = Node(item)

            cur = self._head
            cur_pos = 0
            while cur.next is not None:
                if cur_pos == (pos - 1):
                    # 与下一个节点互相指向
                    node.next = cur.next
                    cur.next.prev = node
                    # 与上一个节点互相指向
                    cur.next = node
                    node.prev = cur
                cur_pos += 1
                cur = cur.next

    def remove(self, item):
        """删除节点"""
        if self.is_empty():
            return
        else:
            cur = self._head
            # 删除首节点
            if cur.item == item:
                self._head = cur.next
                cur.next.prev = None

            # 删除其他节点
            else:
                while cur.next is not None:
                    if cur.item == item:
                        # 删除之前：1 ←→ [2] ←→ 3
                        # 删除之后：1 ←→ 3
                        cur.prev.next = cur.next
                        cur.next.prev = cur.prev
                    cur = cur.next

                # 删除尾节点
                if cur.item == item:
                    cur.prev.next = None


    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return -1
        else:
            cur = self._head
            cur_pos = 0
            while cur.next is not None:
                if cur.item == item:
                    return cur_pos

                cur_pos += 1
                cur = cur.next

            if cur_pos == (self.length() - 1):
                return -1


if __name__ == "__main__":
    ll = DLinkList()
    ll.add(1)       # 1
    ll.add(2)       # 2 1
    ll.append(3)    # 2 1 3
    ll.insert(2, 4) # 2 1 4 3
    ll.insert(4, 5) # 2 1 4 3 5
    ll.insert(0, 6) # 6 2 1 4 3 5
    print("length:", ll.length())   # 6
    ll.travel()                 # 6 2 1 4 3 5
    print("search(3)", ll.search(3))
    print("search(4)", ll.search(4))
    print("search(10)", ll.search(10))
    ll.remove(1)
    print("length:", ll.length())
    ll.travel()
    print("删除首节点 remove(6)：")
    ll.remove(6)
    ll.travel()
    print("删除尾节点 remove(5)：")
    ll.remove(5)
    ll.travel()