[学习笔记]各种口味的线段树(一)
壹. 平凡的线段树
考虑一个数列 \(A={10,11,12,13,14}\)
线段树之所以称为“树”,是因为其具有树的结构特性
线段树本身是专门用来处理区间问题的
对于每一个线段树的子节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息
子节点不断向自己的父亲节点传递信息,而父节点存储的信息则是他的每一个子节点信息的整合。
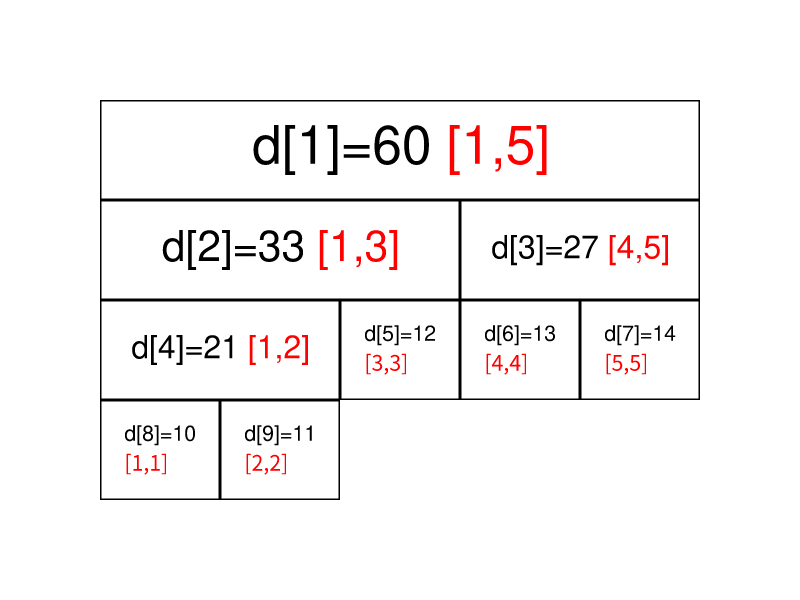
线段树就是分块思想的树化,或者说是对于信息处理的二进制化
通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成 \(k\) 个所分块与 \(m\) 个单个元素的信息的并
线段树可以通过类似于二分的修改、查询操作让这两个复杂度都变成 \(\mathcal{O}(\log n)\)
然而我们发现如果在每次操作时都硬更新时间复杂度会达到恐怖的 \(\mathcal{O}(n\log n)\) ,所以引入一个叫做 懒标记 的玩意,每次逐级下放达到目的
当然这篇博客不是讲普通线段树的,因此请移步 皎月半洒花巨佬的洛谷日报
但为了我个人复习用还是要丢一个模板上来
居然挂了两发我是不是要凉了
点击查看代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<iostream>
#define WR WinterRain
#define int long long
using namespace std;
const int WR=1001000,INF=1099511627776;
struct SegmentTree{
int l,r,val,lzy;
}tree[WR<<2];
int n,m;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].val=tree[k<<1].val+tree[k<<1|1].val;
}
void pushdown(int k){//下放懒标记
tree[k<<1].val+=(tree[k<<1].r-tree[k<<1].l+1)*tree[k].lzy;
tree[k<<1|1].val+=(tree[k<<1|1].r-tree[k<<1|1].l+1)*tree[k].lzy;
tree[k<<1].lzy+=tree[k].lzy;
tree[k<<1|1].lzy+=tree[k].lzy;
tree[k].lzy=0;
}
void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
if(l==r){
tree[k].val=a[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify(int k,int l,int r,int val){//区间修改
if(tree[k].l>=l&&tree[k].r<=r){
tree[k].val+=(tree[k].r-tree[k].l+1)*val;
tree[k].lzy+=val;//注意是+=
return;
}
if(tree[k].lzy) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify(k<<1,l,r,val);
if(r>mid) modify(k<<1|1,l,r,val);
pushup(k);
}
int query(int k,int l,int r){//区间查询
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].val;
}
if(tree[k].lzy) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=0;
if(l<=mid) res+=query(k<<1,l,r);
if(r>mid) res+=query(k<<1|1,l,r);
return res;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++){
int opt=read();
if(opt==1){
int l=read(),r=read(),val=read();
modify(1,l,r,val);
}else{
int l=read(),r=read();
printf("%lld\n",query(1,l,r));
}
}
return 0;
}
需要维护两个懒标记:一个记录乘法,一个记录加法
点击查看代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<iostream>
#define WR WinterRain
#define int long long
using namespace std;
const int WR=101000,INF=1099511627776;
struct SegmentTree{
int l,r,val,mullzy,addlzy;
SegmentTree(){l=r=val=addlzy=0,mullzy=1;}
}tree[WR<<2];
int n,m,mod;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].val=(tree[k<<1].val+tree[k<<1|1].val)%mod;
}
void pushdown(int k){
tree[k<<1].val=(tree[k<<1].val*tree[k].mullzy%mod+tree[k].addlzy*(tree[k<<1].r-tree[k<<1].l+1)%mod)%mod;
tree[k<<1|1].val=(tree[k<<1|1].val*tree[k].mullzy%mod+tree[k].addlzy*(tree[k<<1|1].r-tree[k<<1|1].l+1)%mod)%mod;
tree[k<<1].mullzy=tree[k<<1].mullzy*tree[k].mullzy%mod;
tree[k<<1|1].mullzy=tree[k<<1|1].mullzy*tree[k].mullzy%mod;
tree[k<<1].addlzy=(tree[k<<1].addlzy*tree[k].mullzy%mod+tree[k].addlzy)%mod;
tree[k<<1|1].addlzy=(tree[k<<1|1].addlzy*tree[k].mullzy%mod+tree[k].addlzy)%mod;
tree[k].mullzy=1,tree[k].addlzy=0;
}
void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
if(l==r){
tree[k].val=a[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify_mul(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
tree[k].val=tree[k].val*val%mod;
tree[k].mullzy=tree[k].mullzy*val%mod;
tree[k].addlzy=tree[k].addlzy*val%mod;
return;
}
if(tree[k].mullzy!=1||tree[k].addlzy!=0) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_mul(k<<1,l,r,val);
if(r>mid) modify_mul(k<<1|1,l,r,val);
pushup(k);
}
void modify_add(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
tree[k].val=(tree[k].val+(tree[k].r-tree[k].l+1)*val%mod)%mod;
tree[k].addlzy=(tree[k].addlzy+val)%mod;
return;
}
if(tree[k].mullzy!=1||tree[k].addlzy!=0) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_add(k<<1,l,r,val);
if(r>mid) modify_add(k<<1|1,l,r,val);
pushup(k);
}
int query(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].val;
}
if(tree[k].mullzy!=1||tree[k].addlzy!=0) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=0;
if(l<=mid) res=(res+query(k<<1,l,r))%mod;
if(r>mid) res=(res+query(k<<1|1,l,r))%mod;
return res;
}
signed main(){
n=read(),m=read(),mod=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++){
int opt=read();
if(opt==1){
int l=read(),r=read(),val=read();
modify_mul(1,l,r,val);
}else if(opt==2){
int l=read(),r=read(),val=read();
modify_add(1,l,r,val);
}else{
int l=read(),r=read();
printf("%lld\n",query(1,l,r));
}
}
return 0;
}
然后就可以挑战一道叫做 山海经 的有趣题目了
其实不难,就是需要求出区间内最大子段和
\(\operatorname{pushup}\) 函数里只需要维护 \(10\) 个变量,简直[数据删除]!
这不还是模板题么,看我秒切 \(\cdots\cdots\) 个头啊!!!
好的,我们引入下一个主题
贰. 吉司机线段树
吉司机线段树就是维护区间最值和区间历史最值的线段树,来源于吉如一巨佬
看这道模板题:
给你一个长度为 \(n\) 的序列 \(a\) ,令序列 \(b=a\)
现在让你进行 \(m\) 次操作,分为 \(5\) 种:
1 l r v:将序列 \(a\) 中区间 \([l,r]\) 的数加上 kkk2 l r v:将序列 \(a\) 中区间 \([l,r]\) 的数对 vvv 取最小值3 l r:求序列 \(a\) 中区间 \([l,r]\) 的数的和4 l r:求序列 \(a\) 中区间 \([l,r]\) 的数的最大值5 l r:求序列 \(b\) 中区间 \([l,r]\) 的数的最大值
每次操作后令 \(b_{i}=\max(b_{i},a_{i})\)
好像很迷惑?那我们从最简单的开始分析
一. 单纯的区间求最值操作
首先假设有一个序列 \(a\)
区间最值操作是指给定 \(l,r,val\) ,将所有 \(i\in[l,r]\) 的 \(a_i\) 对 \(val\) 取 \(\min\)(或者 \(\max\))
考虑一道题目
HDU5306 Gorgeous Sequence \(\gets\) 别点了,\(HDU\) 崩了
请你维护一个序列 \(a\) ,支持 \(3\) 种操作
\(\mathfrak{1.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其变为 \(\min(a_i,val)\)
\(\mathfrak{2.}\) 给定 \(l,r\) ,求区间最大值
\(\mathfrak{3.}\) 给定 \(l,r\) ,求 \(\sum\limits_{i=l}^{r}a_i\)
考虑到区间取 \(\min\) 的操作只会对最大值超过 \(k\) 的节点产生影响,我们可以在这方面找一想法
线段树的一个节点需要维护四个信息:
区间和 \(val\) ,区间最大值 \(maxval\) ,区间严格次大值 \(sndmax\) 和最大值的个数 \(maxcnt\)
那么,一次区间最值操作作用在这个节点上时,可以被分为以下三种情况:
- \(val\geqslant maxval\) 显然没有任何作用,直接返回
- \(sndmax<val<maxval\) 此时该节点代表区间的最大值被修改为 \(val\) ,区间和加上 \(maxcnt\times (maxval-val)\),打个懒标记回溯即可
- \(val\leqslant sndmax\) 此时无法快速更新区间信息,因此需要继续递归到左右子树中,回溯时合并信息
举个例子,现在要以 \(k=2\) 对下面这棵线段树维护的区间取 \(\min\)
每个节点左侧表示区间最大值,右侧表示严格次大值。
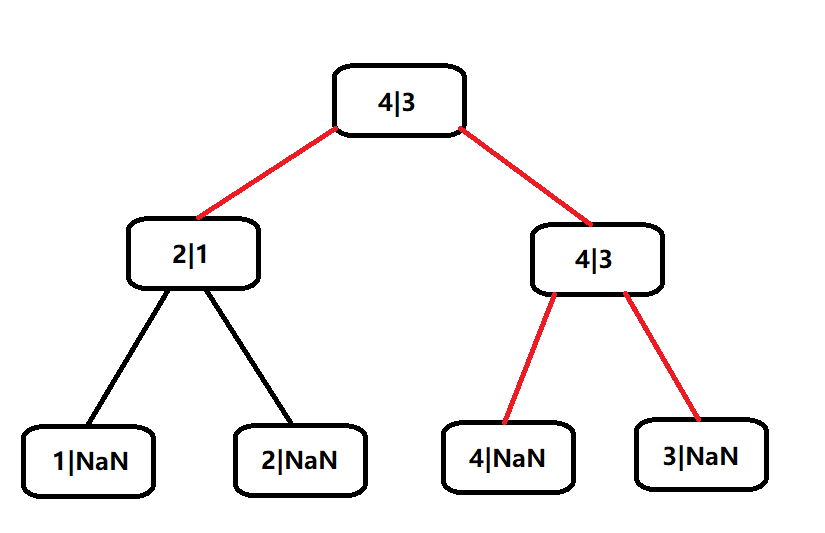
按照上面描述的操作,我们应该沿着红色的边 DFS,最后在红色的节点上更新区间和并打上标记。
点击查看代码
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000,INF=1099511627776;
struct SegmentTree{
int l,r,maxval,sndmax,maxcnt,val,lzy;
}tree[WR<<2];
int n,m;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].val=tree[k<<1].val+tree[k<<1|1].val;
if(tree[k<<1].maxval==tree[k<<1|1].maxval){//如果左右子树最大值相等
tree[k].maxval=tree[k<<1].maxval;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].sndmax);//次大值取左右子树次大值的最大值
tree[k].maxcnt=tree[k<<1].maxcnt+tree[k<<1|1].maxcnt;
}else if(tree[k<<1].maxval>tree[k<<1|1].maxval){//如果左子树最大值为区间最大值
tree[k].maxval=tree[k<<1].maxval;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].maxval);//次大值取左子树次大值和右子树最大值的最大值
tree[k].maxcnt=tree[k<<1].maxcnt;
}else{
tree[k].maxval=tree[k<<1|1].maxval;
tree[k].sndmax=max(tree[k<<1].maxval,tree[k<<1|1].sndmax);
tree[k].maxcnt=tree[k<<1|1].maxcnt;
}
}
void update(int k,int val){
if(tree[k].maxval<=val) return;
tree[k].val-=(tree[k].maxval-val)*tree[k].maxcnt;
tree[k].maxval=tree[k].lzy=val;
}
void pushdown(int k){
update(k<<1,tree[k].lzy);
update(k<<1|1,tree[k].lzy);
tree[k].lzy=-1;//重置懒标记
}
void build(int k,int l,int r){
tree[k].lzy=-1,tree[k].l=l,tree[k].r=r;
if(l==r){
tree[k].val=tree[k].maxval=a[l];
tree[k].sndmax=-1;
tree[k].maxcnt=1;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify(int k,int l,int r,int val){
if(val>=tree[k].maxval) return;//情况 1
if(tree[k].l>=l&&tree[k].r<=r&&tree[k].sndmax<val){//情况 2
update(k,val);
return;
}
if(tree[k].lzy!=-1) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;//情况 3
if(l<=mid) modify(k<<1,l,r,val);//继续下放
if(r>mid) modify(k<<1|1,l,r,val);
pushup(k);
}
int query_max(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].maxval;
}
if(tree[k].lzy!=-1) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_max(k<<1,l,r));
if(r>mid) res=max(res,query_max(k<<1|1,l,r));
return res;
}
int query_sum(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].val;
}
if(tree[k].lzy!=-1) pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=0;
if(l<=mid) res+=query_sum(k<<1,l,r);
if(r>mid) res+=query_sum(k<<1|1,l,r);
return res;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++){
int opt=read();
if(opt==0){
int l=read(),r=read(),val=read();
modify(1,l,r,val);
}else if(opt==1){
int l=read(),r=read();
printf("%lld\n",query_max(1,l,r));
}else{
int l=read(),r=read();
printf("%lld\n",query_sum(1,l,r));
}
}
return 0;
}
二. 考虑加入加减操作
请你维护一个序列 \(a\) ,支持 \(6\) 种操作
\(\mathfrak{1.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其加上 \(val\)
\(\mathfrak{2.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其变为 \(\max(a_i,val)\)
\(\mathfrak{3.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其变为 \(\min(a_i,val)\)
\(\mathfrak{4.}\) 给定 \(l,r\) ,求 \(\sum\limits_{i=l}^{r}a_i\)
\(\mathfrak{5.}\) 给定 \(l,r\) ,求区间最大值
\(\mathfrak{6.}\) 给定 \(l,r\) ,求区间最小值
注意到了区间取最值同时出现了,显然地我们可以维护多一倍的标记维护新值,但相应的,
码量也会多一倍
这无疑是坏的,因此我们考虑如何缩减程序
应这道题的需要,我们将一个区间的元素划分为最大值、最小值和其他值三种
首先在每个节点上肯定要维护区间和 \(val\) ,区间最大值 \(maxval\) 和最小值 \(minval\) 的信息
同时我们也要维护次大值 \(sndmax\) ,次小值 \(sndmin\) 和最大值最小值的个数 \(cntmax,cntmin\)
我们分别讨论题目中的三种修改操作:
- 对于加减操作,在线段树上定位区间后直接对三类值同时加上 \(val\)
- 对于取最小值操作,在线段树上暴力搜索找到 \(sndmax<val<maxval\) 的节点;这些节点对应的区间的最大值都应该改成 \(val\) ,只对最大值加上 \(val-maxval\) 即可
- 对于取最大值操作,同理
但是有一些要注意的地方:
- 以最大值上的加减标记为例,下传这个标记时要判断子区间内是否包含最大值,如果不包含则应下传其他值的加减标记;
- 如果一个区间的值域很小,可能会发生一个值既是最大值又是次小值这种情况,这种情况要特判,分辨到底该被哪个标记作用。
为了不至于混乱,我们开 \(3\) 个懒标记记录有关数值
点击查看代码
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=501000,INF=1099511627776;
struct SegmentTree{
int l,r,val,lzy;
int maxval,sndmax,maxcnt,maxlzy;
int minval,sndmin,mincnt,minlzy;
}tree[WR*5];
int n,m;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].val=tree[k<<1].val+tree[k<<1|1].val;
if(tree[k<<1].maxval==tree[k<<1|1].maxval){
tree[k].maxval=tree[k<<1].maxval;
tree[k].maxcnt=tree[k<<1].maxcnt+tree[k<<1|1].maxcnt;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].sndmax);
}else if(tree[k<<1].maxval>tree[k<<1|1].maxval){
tree[k].maxval=tree[k<<1].maxval;
tree[k].maxcnt=tree[k<<1].maxcnt;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].maxval);
}else{
tree[k].maxval=tree[k<<1|1].maxval;
tree[k].maxcnt=tree[k<<1|1].maxcnt;
tree[k].sndmax=max(tree[k<<1].maxval,tree[k<<1|1].sndmax);
}
if(tree[k<<1].minval==tree[k<<1|1].minval){
tree[k].minval=tree[k<<1].minval;
tree[k].mincnt=tree[k<<1].mincnt+tree[k<<1|1].mincnt;
tree[k].sndmin=min(tree[k<<1].sndmin,tree[k<<1|1].sndmin);
}else if(tree[k<<1].minval<tree[k<<1|1].minval){
tree[k].minval=tree[k<<1].minval;
tree[k].mincnt=tree[k<<1].mincnt;
tree[k].sndmin=min(tree[k<<1].sndmin,tree[k<<1|1].minval);
}else{
tree[k].minval=tree[k<<1|1].minval;
tree[k].mincnt=tree[k<<1|1].mincnt;
tree[k].sndmin=min(tree[k<<1].minval,tree[k<<1|1].sndmin);
}
}
void update(int k,int valmin,int valmax,int valsum){
if(tree[k].minval==tree[k].maxval){
if(valmin==valsum) valmin=valmax;
else valmax=valmin;//在只有一个值的时候不应被其他值的标记作用
tree[k].val+=valmin*tree[k].mincnt;//因此找那个非 0 的标记
}else tree[k].val+=valmin*tree[k].mincnt+valmax*tree[k].maxcnt+
valsum*(tree[k].r-tree[k].l+1-tree[k].maxcnt-tree[k].mincnt);
if(tree[k].sndmax==tree[k].minval) tree[k].sndmax+=valmin;
else if(tree[k].sndmax!=-INF) tree[k].sndmax+=valsum;
if(tree[k].sndmin==tree[k].maxval) tree[k].sndmin+=valmax;//次小值等于最大值,应该被最大值标记作用
else if(tree[k].sndmin!=INF) tree[k].sndmin+=valsum;//否则应该被其他值标记作用
tree[k].maxval+=valmax,tree[k].minval+=valmin;
tree[k].maxlzy+=valmax,tree[k].minlzy+=valmin,tree[k].lzy+=valsum;
}
void pushdown(int k){
int minn=min(tree[k<<1].minval,tree[k<<1|1].minval);
int maxx=max(tree[k<<1].maxval,tree[k<<1|1].maxval);
update(k<<1,tree[k<<1].minval==minn?tree[k].minlzy:tree[k].lzy,
tree[k<<1].maxval==maxx?tree[k].maxlzy:tree[k].lzy,tree[k].lzy);
update(k<<1|1,tree[k<<1|1].minval==minn?tree[k].minlzy:tree[k].lzy,
tree[k<<1|1].maxval==maxx?tree[k].maxlzy:tree[k].lzy,tree[k].lzy);
tree[k].maxlzy=tree[k].minlzy=tree[k].lzy=0;
}
void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
tree[k].maxlzy=tree[k].minlzy=tree[k].lzy=0;
if(l==r){
tree[k].val=tree[k].maxval=tree[k].minval=a[l];
tree[k].sndmin=INF,tree[k].sndmax=-INF;
tree[k].maxcnt=tree[k].mincnt=1;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify_sum(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
update(k,val,val,val);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_sum(k<<1,l,r,val);
if(r>mid) modify_sum(k<<1|1,l,r,val);
pushup(k);
}
void modify_min(int k,int l,int r,int val){
if(val>=tree[k].maxval) return;
if(tree[k].l>=l&&tree[k].r<=r&&val>tree[k].sndmax){
update(k,0,val-tree[k].maxval,0);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_min(k<<1,l,r,val);
if(r>mid) modify_min(k<<1|1,l,r,val);
pushup(k);
}
void modify_max(int k,int l,int r,int val){
if(val<=tree[k].minval) return;
if(tree[k].l>=l&&tree[k].r<=r&&val<tree[k].sndmin){
update(k,val-tree[k].minval,0,0);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_max(k<<1,l,r,val);
if(r>mid) modify_max(k<<1|1,l,r,val);
pushup(k);
}
int query_sum(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].val;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=0;
if(l<=mid) res+=query_sum(k<<1,l,r);
if(r>mid) res+=query_sum(k<<1|1,l,r);
return res;
}
int query_max(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].maxval;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_max(k<<1,l,r));
if(r>mid) res=max(res,query_max(k<<1|1,l,r));
return res;
}
int query_min(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].minval;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=INF;
if(l<=mid) res=min(res,query_min(k<<1,l,r));
if(r>mid) res=min(res,query_min(k<<1|1,l,r));
return res;
}
signed main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
m=read();
for(int i=1;i<=m;i++){
int opt=read();
if(opt==1){
int l=read(),r=read(),val=read();
modify_sum(1,l,r,val);
}
if(opt==2){
int l=read(),r=read(),val=read();
modify_max(1,l,r,val);
}
if(opt==3){
int l=read(),r=read(),val=read();
modify_min(1,l,r,val);
}
if(opt==4){
int l=read(),r=read();
printf("%lld\n",query_sum(1,l,r));
}
if(opt==5){
int l=read(),r=read();
printf("%lld\n",query_max(1,l,r));
}
if(opt==6){
int l=read(),r=read();
printf("%lld\n",query_min(1,l,r));
}
}
return 0;
}
三. 区间历史最值问题
请你维护一个序列 \(a\) 和一个辅助序列 \(b\) (最开始 \(b=a\) ),支持 \(4\) 种操作
\(\mathfrak{1.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其加上 \(val\)
\(\mathfrak{2.}\) 给定 \(l,r,val\) ,对于所有 \(i\in [l,r]\) 的 \(a_i\) ,将其变为 \(val\)
\(\mathfrak{3.}\) 给定 \(l,r\) ,求 \(a\) 的区间最大值
\(\mathfrak{4.}\) 给定 \(l,r\) ,求 \(b\) 的区间最大值
每次操作后,将所有 \(b_i\) 变为 \(\max(a_i,b_i)\)
考虑如何维护历史最值
显然地,我们要维护最大值 \(maxval\) ,历史最大值 \(hismax\) 和区间加标记 \(maxlzy\)
同时我们还需要维护一个 \(hislzy\) ,用来维护从上一次下传 \(maxlzy\) 到现在,区间加标记达到的最大值。
考虑如何合并?
现在加入区间覆盖操作,我们把标记换成 \((maxlzy,covval)\) 表示将当前区间先加上 \(maxlzy\) 再全部变成 \(covval\)
这个标记是可以合并的:如果一个区间已经被覆盖成了一个值,那么区间加操作可以转化为区间覆盖操作,直接把它加到 \(covval\) 上即可。
同理,我们还需要维护 \((hislzy,hiscov)\)
表示上一次下传这个节点的标记到现在,区间加的最大值为 \(hislzy\) ,区间覆盖的最大值为 \(hiscov\)
点击查看代码
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=501000,INF=1099511627776;
struct SegmentTree{
int l,r;
int maxval,maxlzy,covval;
int hismax,hislzy,hiscov;
bool tag;
}tree[WR<<2];
int n,q;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].maxval=max(tree[k<<1].maxval,tree[k<<1|1].maxval);
tree[k].hismax=max(tree[k<<1].hismax,tree[k<<1|1].hismax);
}
void update_plus(int k,int val,int hisval){
tree[k].hismax=max(tree[k].hismax,tree[k].maxval+hisval);
tree[k].maxval+=val;
if(!tree[k].tag) tree[k].hislzy=max(tree[k].hislzy,tree[k].maxlzy+hisval),tree[k].maxlzy+=val;
else tree[k].hiscov=max(tree[k].hiscov,tree[k].covval+hisval),tree[k].covval+=val;
}
void update_cover(int k,int val,int hisval){
tree[k].hismax=max(tree[k].hismax,hisval);
tree[k].maxval=val;
tree[k].hiscov=max(tree[k].hiscov,hisval);
tree[k].covval=val;
tree[k].tag=true;
}
void pushdown(int k){
if(tree[k].maxlzy){
update_plus(k<<1,tree[k].maxlzy,tree[k].hislzy);
update_plus(k<<1|1,tree[k].maxlzy,tree[k].hislzy);
tree[k].maxlzy=tree[k].hislzy=0;
}
if(tree[k].tag){
update_cover(k<<1,tree[k].covval,tree[k].hiscov);
update_cover(k<<1|1,tree[k].covval,tree[k].hiscov);
tree[k].tag=false;
tree[k].hiscov=-INF;
}
}
void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
tree[k].maxlzy=tree[k].hislzy=tree[k].tag=0;
tree[k].hiscov=-INF;
if(l==r){
tree[k].maxval=tree[k].hismax=a[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify_plus(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
update_plus(k,val,val);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_plus(k<<1,l,r,val);
if(r>mid) modify_plus(k<<1|1,l,r,val);
pushup(k);
}
void modify_cover(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
update_cover(k,val,val);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_cover(k<<1,l,r,val);
if(r>mid) modify_cover(k<<1|1,l,r,val);
pushup(k);
}
int query_max(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].maxval;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_max(k<<1,l,r));
if(r>mid) res=max(res,query_max(k<<1|1,l,r));
return res;
}
int query_his(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].hismax;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_his(k<<1,l,r));
if(r>mid) res=max(res,query_his(k<<1|1,l,r));
return res;
}
signed main(){
// freopen("test.in", "r", stdin);
// freopen("cpp.out", "w", stdout);
n=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
q=read();
while(q--){
char str[5];
scanf("%s",str+1);
if(str[1]=='Q'){
int l=read(),r=read();
printf("%lld\n",query_max(1,l,r));
}
if(str[1]=='A'){
int l=read(),r=read();
printf("%lld\n",query_his(1,l,r));
}
if(str[1]=='P'){
int l=read(),r=read(),val=read();
modify_plus(1,l,r,val);
}
if(str[1]=='C'){
int l=read(),r=read(),val=read();
modify_cover(1,l,r,val);
}
}
return 0;
}
四. 加入区间最值操作
终于到了我们的模板
P6242 【模板】线段树 3
考虑维护 \(4\) 个标记
- 最大值加减标记 \(maxlzy\)
- 最大值历史最大的加减标记 \(hismaxlzy\)
- 非最大值加减标记 \(lzy\)
- 非最大值历史最大的加减标记 \(hislzy\)
然后结合上面的内容就可以比较轻易地做出来
点击查看代码
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<vector>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=501000,INF=1099511627776;
struct SegmentTree{
int l,r,val,lzy;
int maxval,sndmax,maxcnt,maxlzy;
int hismax,hismaxlzy,hislzy;
}tree[WR<<2];
int n,q;
int a[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<3)+(s<<1)+ch-'0';
ch=getchar();
}
return s*w;
}
void pushup(int k){
tree[k].val=tree[k<<1].val+tree[k<<1|1].val;
tree[k].hismax=max(tree[k<<1].hismax,tree[k<<1|1].hismax);
if(tree[k<<1].maxval==tree[k<<1|1].maxval){
tree[k].maxval=tree[k<<1].maxval;
tree[k].maxcnt=tree[k<<1].maxcnt+tree[k<<1|1].maxcnt;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].sndmax);
}else if(tree[k<<1].maxval>tree[k<<1|1].maxval){
tree[k].maxval=tree[k<<1].maxval;
tree[k].maxcnt=tree[k<<1].maxcnt;
tree[k].sndmax=max(tree[k<<1].sndmax,tree[k<<1|1].maxval);
}else{
tree[k].maxval=tree[k<<1|1].maxval;
tree[k].maxcnt=tree[k<<1|1].maxcnt;
tree[k].sndmax=max(tree[k<<1].maxval,tree[k<<1|1].sndmax);
}
}
void update(int k,int lzy,int hislzy,int maxlzy,int hismaxlzy){
tree[k].val+=maxlzy*tree[k].maxcnt+lzy*(tree[k].r-tree[k].l+1-tree[k].maxcnt);
tree[k].hismax=max(tree[k].hismax,tree[k].maxval+hismaxlzy);
tree[k].hismaxlzy=max(tree[k].hismaxlzy,tree[k].maxlzy+hismaxlzy);
tree[k].maxval+=maxlzy,tree[k].maxlzy+=maxlzy;
tree[k].hislzy=max(tree[k].hislzy,tree[k].lzy+hislzy);
if(tree[k].sndmax!=-INF) tree[k].sndmax+=lzy;
tree[k].lzy+=lzy;
}
void pushdown(int k){
int maxx=max(tree[k<<1].maxval,tree[k<<1|1].maxval);
update(k<<1,tree[k].lzy,tree[k].hislzy,
tree[k<<1].maxval==maxx?tree[k].maxlzy:tree[k].lzy,
tree[k<<1].maxval==maxx?tree[k].hismaxlzy:tree[k].hislzy);
update(k<<1|1,tree[k].lzy,tree[k].hislzy,
tree[k<<1|1].maxval==maxx?tree[k].maxlzy:tree[k].lzy,
tree[k<<1|1].maxval==maxx?tree[k].hismaxlzy:tree[k].hislzy);
tree[k].lzy=tree[k].maxlzy=tree[k].hislzy=tree[k].hismaxlzy=0;
}
void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
tree[k].lzy=tree[k].maxlzy=tree[k].hislzy=tree[k].hismaxlzy=0;
if(l==r){
tree[k].val=tree[k].maxval=tree[k].hismax=a[l];
tree[k].sndmax=-INF,tree[k].maxcnt=1;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
pushup(k);
}
void modify_sum(int k,int l,int r,int val){
if(tree[k].l>=l&&tree[k].r<=r){
update(k,val,val,val,val);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_sum(k<<1,l,r,val);
if(r>mid) modify_sum(k<<1|1,l,r,val);
pushup(k);
}
void modify_min(int k,int l,int r,int val){
if(tree[k].maxval<=val) return;
if(tree[k].l>=l&&tree[k].r<=r&&val>tree[k].sndmax){
update(k,0,0,val-tree[k].maxval,val-tree[k].maxval);
return;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid) modify_min(k<<1,l,r,val);
if(r>mid) modify_min(k<<1|1,l,r,val);
pushup(k);
}
int query_sum(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].val;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=0;
if(l<=mid) res+=query_sum(k<<1,l,r);
if(r>mid) res+=query_sum(k<<1|1,l,r);
return res;
}
int query_max(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].maxval;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_max(k<<1,l,r));
if(r>mid) res=max(res,query_max(k<<1|1,l,r));
return res;
}
int query_hismax(int k,int l,int r){
if(tree[k].l>=l&&tree[k].r<=r){
return tree[k].hismax;
}
pushdown(k);
int mid=(tree[k].l+tree[k].r)>>1,res=-INF;
if(l<=mid) res=max(res,query_hismax(k<<1,l,r));
if(r>mid) res=max(res,query_hismax(k<<1|1,l,r));
return res;
}
signed main(){
// freopen("test.in","r",stdin);
// freopen("cpp.out","w",stdout);
n=read(),q=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
while(q--){
int opt=read();
if(opt==1){
int l=read(),r=read(),val=read();
modify_sum(1,l,r,val);
}
if(opt==2){
int l=read(),r=read(),val=read();
modify_min(1,l,r,val);
}
if(opt==3){
int l=read(),r=read();
printf("%lld\n",query_sum(1,l,r));
}
if(opt==4){
int l=read(),r=read();
printf("%lld\n",query_max(1,l,r));
}
if(opt==5){
int l=read(),r=read();
printf("%lld\n",query_hismax(1,l,r));
}
}
return 0;
}
本文来自博客园,作者:冬天的雨WR,转载请注明原文链接:https://www.cnblogs.com/WintersRain/p/16753206.html
为了一切不改变的理想,为了改变不理想的一切

 浙公网安备 33010602011771号
浙公网安备 33010602011771号