[学习笔记]笛卡尔树

笛卡尔树是一种二叉树，每一个结点由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质，而 \(w\) 满足堆的性质

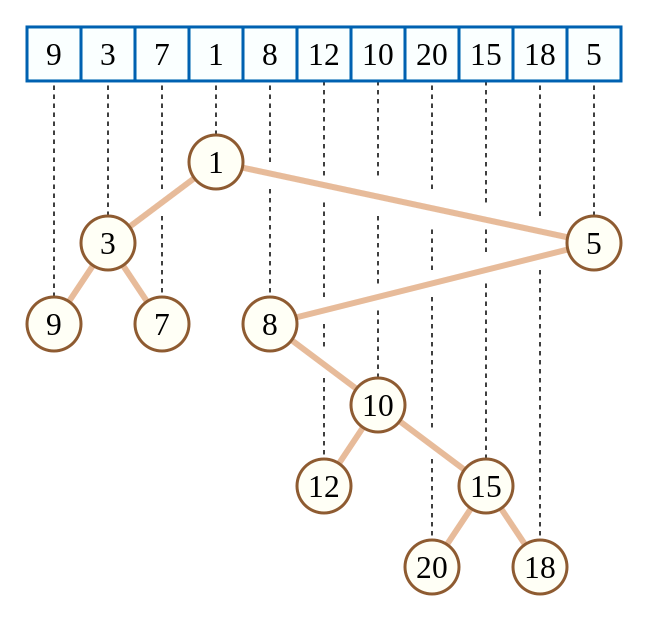
比如这就是一棵以下标为 \(k\) ，元素值为 \(w\) 的二元组构建的笛卡尔树
在保证 \(x_i\) 递增的情况下，我们可以在线性时间复杂度内构造一棵笛卡尔树
每次插入一个新节点时，为了确保二叉搜索树的性质得到满足（别忘了我们按照 xxx 递增的顺序插入），我们需要将新节点一个一个插入到当前的笛卡尔树中
那么每次我们插入的元素必然在这个树的右链（右链：即从根结点一直往右子树走，经过的结点形成的链）的末端
更具体地来说，我们设当前要插入的点为 \(u\)，则我们需要在这个链上找到第一个 \(w\) 权值比 \(w_u\) 小的点 \(v\)，将 \(v\) 的右儿子设置为 \(u\)（如果不存在这样的点，那 \(u\) 就成为根节点了）
然后将 \(v\) 的右子树接在 \(u\) 的左子树下面（因为之前插入的点的 \(k\) 权值都比 \(u_k\) 小，因此这样不会破坏二叉搜索树的性质）
维护这样一条链可以用栈实现。因为每个节点最多进栈出栈各一次，总时间复杂度是 \(\Theta(n)\) 的
下面是建树过程

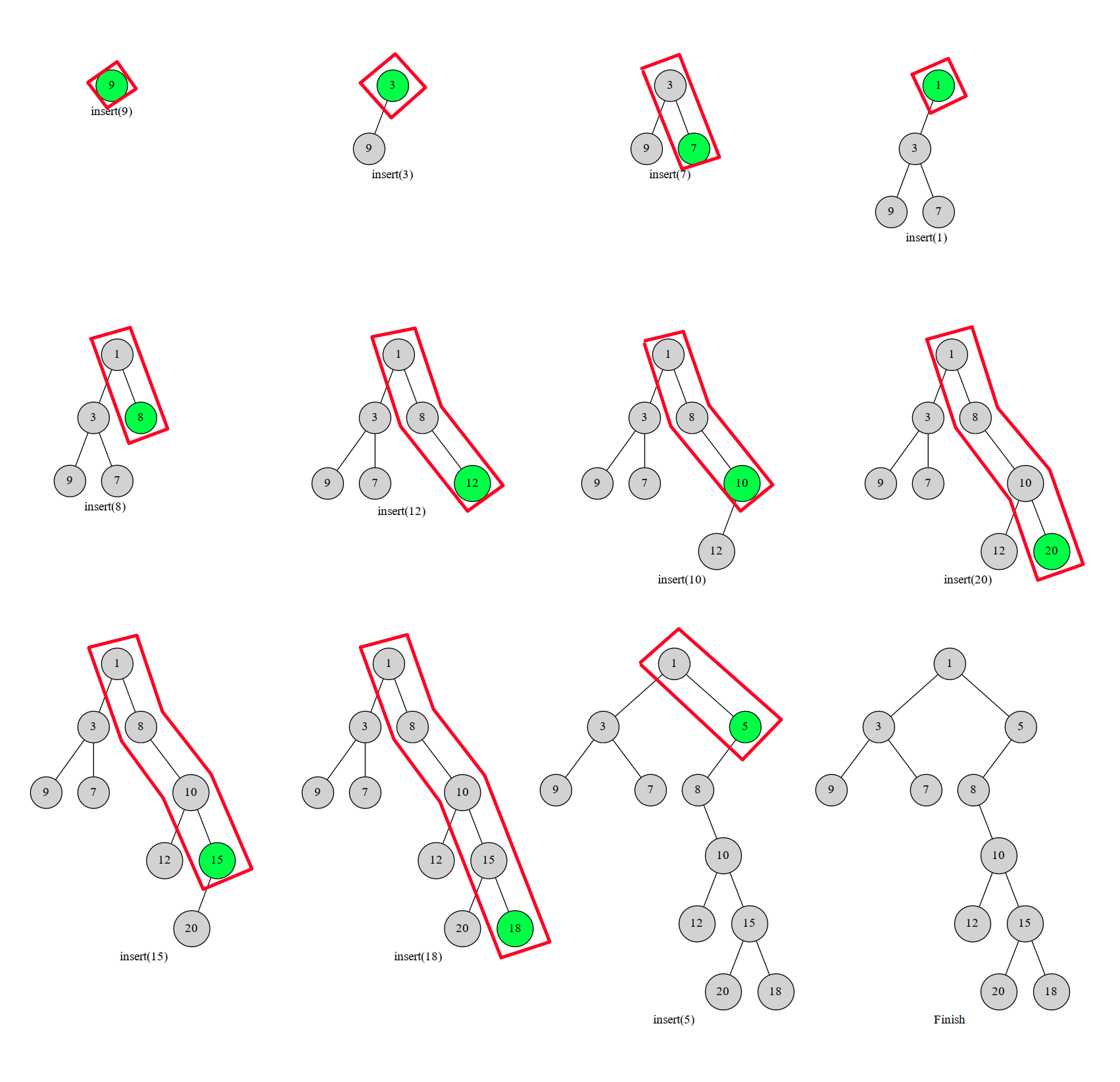
建树可以用单调栈维护一个权值单调递增的下标序列，从栈顶向底部遍历
插入一个点时作为右儿子插入到第一个比它小的点（如果有的话）后，如果遇到了比它大的点，将最后一个比它大的点作为左儿子

for(int i=1;i<=n;i++){
    a[i]=read();
    pos=top;
    while(pos&&a[stk[pos]]>a[i]) pos--;
    if(pos) tree[stk[pos]].r=i;
    if(pos<top) tree[i].l=stk[pos+1];
    stk[++pos]=i;
    top=pos;
}

还是看一道模板题：

P5854 【模板】笛卡尔树

注意到只要单纯地建树即可

点击查看代码

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<vector>
#include<deque>
#include<stack>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=10001000,mod=1e9+7,INF=1099511627776;
struct Cartesian_Tree{
    int l,r;
}tree[WR];
int n;
int stk[WR],top,pos;
int a[WR];
int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch>'9'||ch<'0'){
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		s=(s<<1)+(s<<3)+ch-'0';
		ch=getchar();
	}
	return s*w;
}
signed main(){
    n=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
        pos=top;
        while(pos&&a[stk[pos]]>a[i]) pos--;
        if(pos) tree[stk[pos]].r=i;
        if(pos<top) tree[i].l=stk[pos+1];
        stk[++pos]=i;
        top=pos;
    }
    int L=0,R=0;
    for(int i=1;i<=n;i++){
        L^=i*(tree[i].l+1);
        R^=i*(tree[i].r+1);
    }
    printf("%lld %lld\n",L,R);
	return 0;
}

那么考虑另外一道题目：

P1377 [TJOI2011] 树的序

也是一道比较板子的题目
那么为什么要建笛卡尔树呢？
因为给定的序列一定是 \(1 \sim n\) 的一个序列，又因为它满足二叉搜索树，那么和我们笛卡尔树中的满足二叉搜索树的性质相同。
一个元素越在序列后边，它在二叉搜索树中的位置越深，换句话说，对于一个数 \(x\) ，在它到根的路径上的点一定在序列的前面
所以可以把第几个插入看做权值 \(w\) 去构建笛卡尔树。

点击查看代码

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<vector>
#include<deque>
#include<stack>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=10001000,mod=1e9+7,INF=1099511627776;
struct Cartesian_Tree{
    int l,r;
}tree[WR];
int n;
int stk[WR],top,pos;
int a[WR];
int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch>'9'||ch<'0'){
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		s=(s<<1)+(s<<3)+ch-'0';
		ch=getchar();
	}
	return s*w;
}
void prior(int x){
    printf("%lld ",x);
    if(tree[x].l) prior(tree[x].l);
    if(tree[x].r) prior(tree[x].r);
}
signed main(){
    n=read();
    for(int i=1;i<=n;i++){
        int x=read();
        a[x]=i;
    }
    for(int i=1;i<=n;i++){
        pos=top;
        while(pos&&a[stk[pos]]>a[i]) pos--;
        if(pos) tree[stk[pos]].r=i;
        if(pos<top) tree[i].l=stk[pos+1];
        stk[++pos]=i;
        top=pos;
    }
    prior(stk[1]);
    printf("\n");
	return 0;
}

差不多就是这些了QWQ