[学习笔记]AC自动机
首先请确保你学会了这些前置知识:
\(\operatorname{Trie}\)树 \(\qquad\) 和 \(\qquad\) \(\operatorname{KMP}\)
然后就可以学习所谓的 \(\mathfrak{AC}\) 自动机了
\(\mathfrak{AC}\) 自动机在初始时会将若干个模式串丢到一个 \(\operatorname{Trie}\) 里,然后在 \(\operatorname{Trie}\) 上建立
这个 \(\operatorname{Trie}\) 就是普通的 \(\operatorname{Trie}\),该怎么建怎么建
void insrt(char *str){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
if(!trie[pos].son[val]) trie[pos].son[val]=++tot;
pos=trie[pos].son[val];
}
trie[pos].ed++;
}
\(\operatorname{Trie}\) 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态
一个结点表示一个状态,\(\operatorname{Trie}\) 的边就是状态的转移
每次沿着 \(\operatorname{Trie}\) 树匹配,匹配到当前位置没有匹配上时,直接跳转到失配指针所指向的位置继续进行匹配
失配指针指向当前节点所代表的串的 "最长"的、"能与后缀匹配"的、"在 \(\textbf{Trie}\) 中出现过"的"前缀"所代表的节点。
所以,\(fail\) 指针类似于 \(\operatorname{KMP}\) 的 失配数组,只不过由单串变为了多串而已。
这个 \(\operatorname{Trie}\) 树的失配指针要怎么求?
可以参考 \(\operatorname{KMP}\) 中构造 \(fail\) 指针的思想
考虑字典树中当前的结点 \(u\) ,\(u\) 的父结点是 \(fa\) ,\(fa\) 通过字符 \(\mathbf{c}\) 的边指向 \(u\) ,即 \(trie[fa].son[c]=u\)
假设深度小于 \(u\) 的所有结点的 \(fail\) 指针都已求得
- 如果 \(trie[fail[fa]].son[c]\) 存在:则让 \(u\) 的 \(fail\) 指针指向 \(trie[fail[fa]].son[c]\) 。相当于在 \(fa\) 和 \(fail[fa]\) 后面加一个字符 \(\mathbf{c}\),分别对应 \(u\) 和 \(fail[u]\)
- 如果 \(trie[fail[fa]].son[c]\) 不存在:那么我们跳到 \(trie[fail[fail[fa]]].son[c]\) 。重复 1 的判断过程,一直跳 \(fail\) 指针直到根结点
- 如果真的找不到,就让 fail 指针指向根结点
void get_fail(){
queue<int>q;//考虑使用队列维护
for(int i=0;i<26;i++){
if(trie[root].son[i]){
trie[trie[root].son[i]].fail=root;
q.push(trie[root].son[i]);
}
}
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(trie[u].son[i]){
trie[trie[u].son[i]].fail=trie[trie[u].fail].son[i];
//子节点的fail指针指向 当前节点的 fail指针所指向的节点 的相同子节点
q.push(trie[u].son[i]);
}else{
trie[u].son[i]=trie[trie[u].fail].son[i];
//当前节点的这个子节点指向 当前节点fail指针 的这个子节点
}
}
}
}
从 \(\mathcal{OI-wiki}\) 上扒来了 \(\operatorname{gif}\)
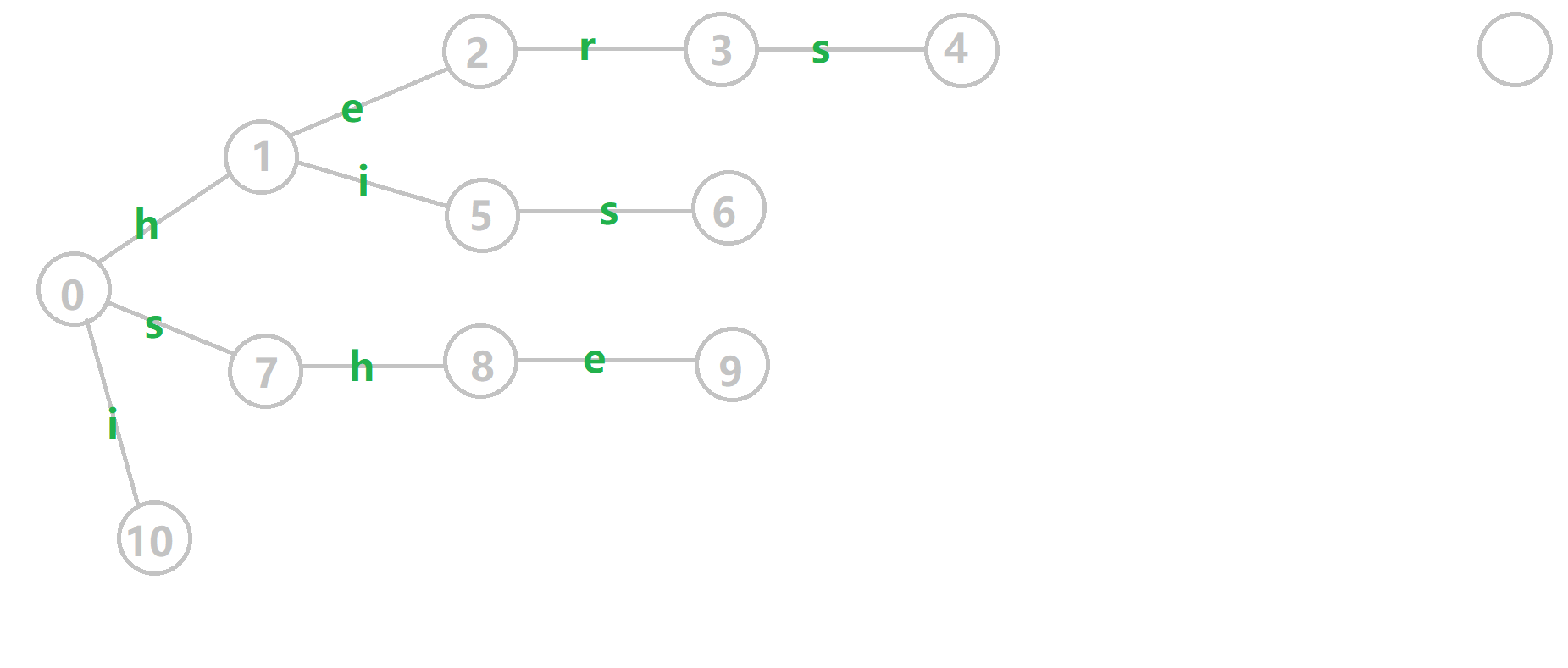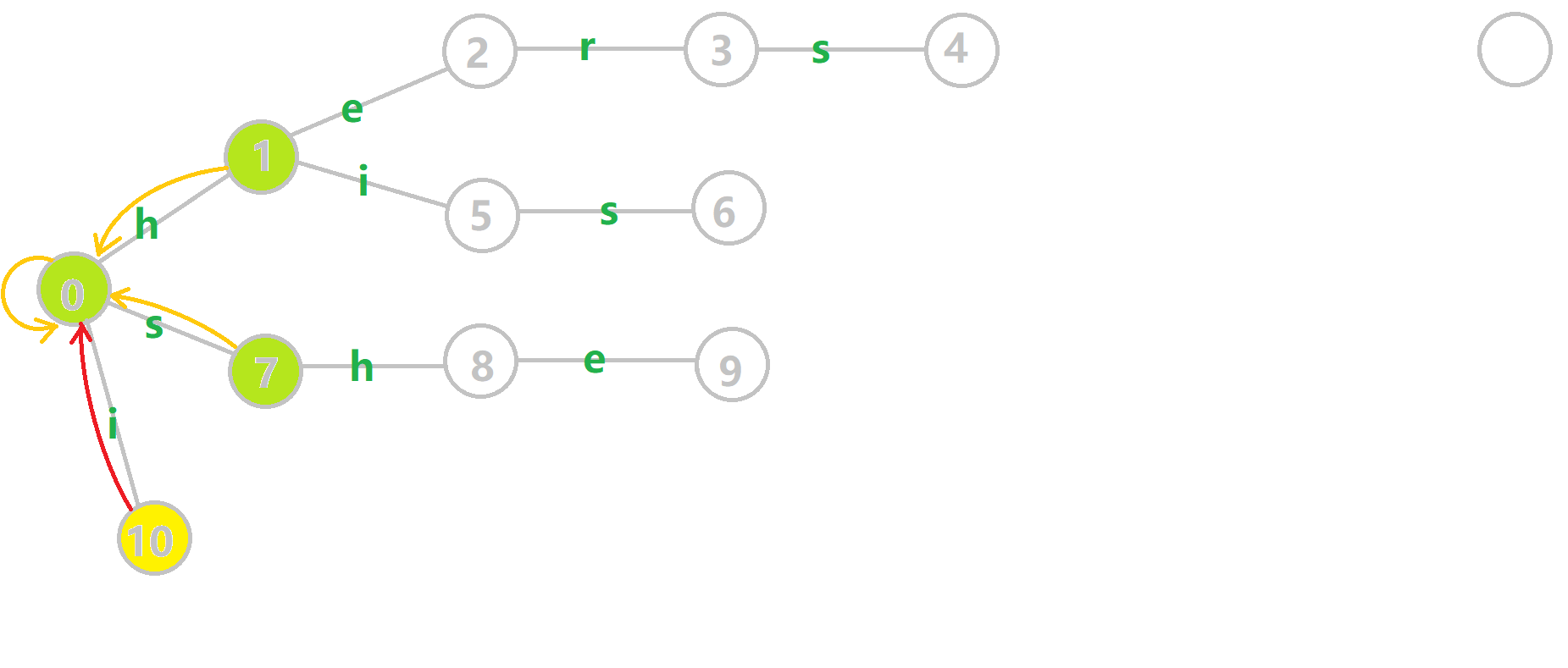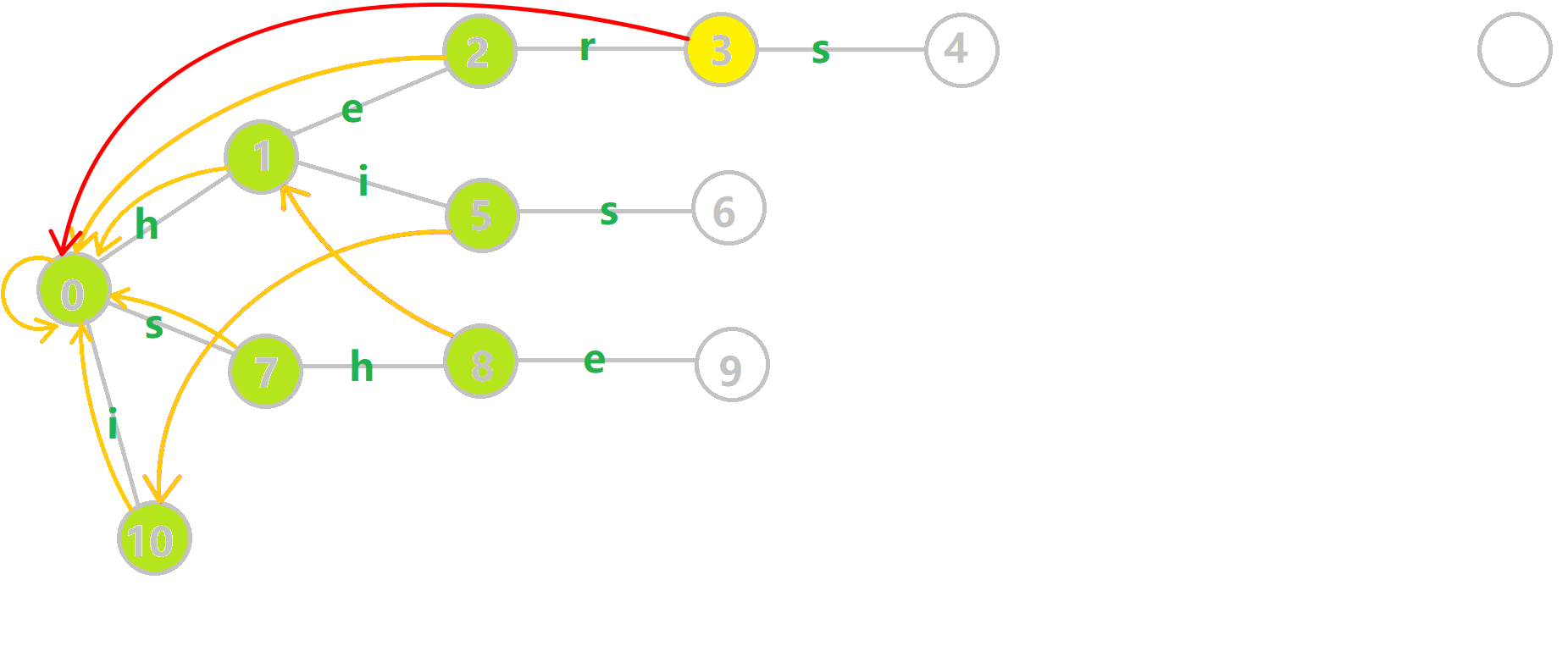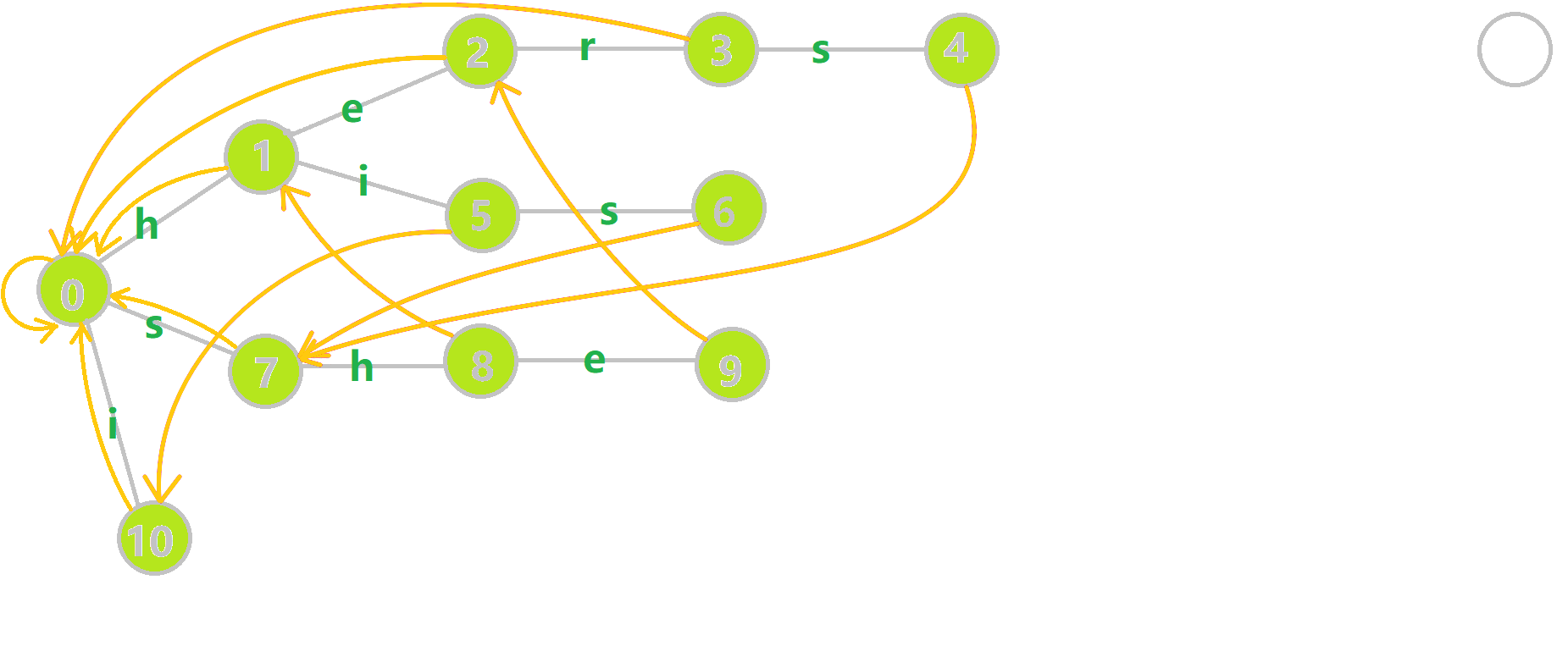
考虑模板题
这里该如何操作?
显然地,我们只要在每个词尾维护一个 \(ed\) 记录其出现次数即可
然后查询时可以轻松地跳 \(fail\) 指针跳到所谓的 "能与后缀匹配的前缀" 上面去
点击查看代码
#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000;
struct AC_automaton{
int fail;
int son[26];
int ed;
}trie[WR];
int n;
int root,tot;
char modu[WR],txt[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<1)+(s<<3)+ch-'0';
ch=getchar();
}
return s*w;
}
void insrt(char *str){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
if(!trie[pos].son[val]) trie[pos].son[val]=++tot;
pos=trie[pos].son[val];
}
trie[pos].ed++;
}
void get_fail(){
queue<int>q;
for(int i=0;i<26;i++){
if(trie[root].son[i]){
trie[trie[root].son[i]].fail=root;
q.push(trie[root].son[i]);
}
}
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(trie[u].son[i]){
trie[trie[u].son[i]].fail=trie[trie[u].fail].son[i];
//子节点的fail指针指向 当前节点的 fail指针所指向的节点 的相同子节点
q.push(trie[u].son[i]);
}else{
trie[u].son[i]=trie[trie[u].fail].son[i];
//当前节点的这个子节点指向 当前节点fail指针 的这个子节点
}
}
}
}
int query(char *str){
int pos=root,res=0,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
pos=trie[pos].son[val];
for(int j=pos;j!=root&&trie[j].ed!=-1;j=trie[j].fail){
res+=trie[j].ed;
trie[j].ed=-1;
}
}
return res;
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
scanf("%s",modu+1);
insrt(modu);
}
root=0;
trie[root].fail=0;
get_fail();
scanf("%s",txt+1);
printf("%lld\n",query(txt));
return 0;
}
显然地只要多开一个结构体维护查询,略作修改就行了
点击查看代码
#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#include<algorithm>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000;
struct AC_automaton{
int fail;
int son[26];
int ed;
}trie[WR];
struct Query{
int id,cnt;
char modu[110];
bool operator<(const Query &b)const{
if(cnt==b.cnt) return id<b.id;
return cnt>b.cnt;
}
}ask[200];
int n;
int root,tot;
char modu[WR],txt[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<1)+(s<<3)+ch-'0';
ch=getchar();
}
return s*w;
}
void insrt(char *str,int id){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
if(!trie[pos].son[val]) trie[pos].son[val]=++tot;
pos=trie[pos].son[val];
}
trie[pos].ed=id;
}
void get_fail(){
queue<int>q;
for(int i=0;i<26;i++){
if(trie[root].son[i]){
trie[trie[root].son[i]].fail=root;
q.push(trie[root].son[i]);
}
}
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(trie[u].son[i]){
trie[trie[u].son[i]].fail=trie[trie[u].fail].son[i];
q.push(trie[u].son[i]);
}else{
trie[u].son[i]=trie[trie[u].fail].son[i];
}
}
}
}
void query(char *str){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
pos=trie[pos].son[val];
for(int j=pos;j!=root;j=trie[j].fail){
ask[trie[j].ed].cnt++;
}
}
}
signed main(){
int n=read();
while(n!=0){
for(int i=0;i<=tot;i++){
for(int j=0;j<26;j++) trie[i].son[j]=0;
trie[i].fail=0;trie[i].ed=0;
}
tot=0;
for(int i=1;i<=n;i++){
scanf("%s",ask[i].modu+1);
ask[i].id=i,ask[i].cnt=0;
insrt(ask[i].modu,i);
}
get_fail();
scanf("%s",txt+1);
query(txt);
sort(ask+1,ask+1+n);
printf("%lld\n",ask[1].cnt);
for(int i=1;i<=n;i++){
if(ask[i].cnt!=ask[1].cnt) break;
printf("%s\n",ask[i].modu+1);
}
n=read();
}
return 0;
}
这个如果硬莽会导致一个 \(\operatorname{LE}\) 的 \(\operatorname{T}\)
让我们把 \(\operatorname{Trie}\)上的 \(fail\) 都想象成一条条有向边
如果在一个点对失配指针指向的点进行一些操作,那么沿着这个点连出去的点也会进行操作(就是跳 \(fail\) )
所以我们才要暴力跳 \(fail\) 去更新之后的点
那么我们可不可以在找到的点打一个标记,最后再一次性将标记全部上传来更新其他点的答案呢?
显然是可以的
那么现在问题来了,怎么确定更新顺序呢?明显我们打了标记后肯定是从深度大的点开始更新上去的。
怎么实现呢?拓扑排序!
我们使每一个点向它的 \(fail\) 指针连一条边,明显,每一个点的出度为 \(1\)( \(fail\) 只有一个),入度可能很多
所以我们就不需要像拓扑排序那样先建个图了,直接往 \(fail\) 指针跳就可以了。
最后我们根据 \(fail\) 指针建好图后(想象一下,程序里不用实现),一定是一个 \(\operatorname{DAG}\)
我们就直接在上面跑拓扑排序,然后更新答案就可以了。
当然还要有统计入度qwq
点击查看代码
#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<queue>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=2001000;
struct AC_automaton{
int fail;
int son[26];
int ed,ans;
}trie[WR];
int n,m;
int root,tot;
int mp[WR],ipt[WR];
int res[WR];
char modu[WR],txt[WR];
int read(){
int s=0,w=1;
char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=(s<<1)+(s<<3)+ch-'0';
ch=getchar();
}
return s*w;
}
void insrt(char *str,int id){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
if(!trie[pos].son[val]) trie[pos].son[val]=++tot;
pos=trie[pos].son[val];
}
if(!trie[pos].ed) trie[pos].ed=id;
mp[id]=trie[pos].ed;
}
void get_fail(){
queue<int>q;
for(int i=0;i<26;i++){
if(trie[root].son[i]){
trie[trie[root].son[i]].fail=root;
q.push(trie[root].son[i]);
}
}
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(trie[u].son[i]){
trie[trie[u].son[i]].fail=trie[trie[u].fail].son[i];
ipt[trie[trie[u].fail].son[i]]++;
q.push(trie[u].son[i]);
}else{
trie[u].son[i]=trie[trie[u].fail].son[i];
}
}
}
}
void query(char *str){
int pos=root,len=strlen(str+1);
for(int i=1;i<=len;i++){
int val=str[i]-'a';
pos=trie[pos].son[val];
trie[pos].ans++;
}
}
void topo(){
queue<int>q;
for(int i=1;i<=tot;i++){
if(ipt[i]==0) q.push(i);
}
while(!q.empty()){
int u=q.front();q.pop();
res[trie[u].ed]=trie[u].ans;
ipt[trie[u].fail]--;
trie[trie[u].fail].ans+=trie[u].ans;
if(ipt[trie[u].fail]==0) q.push(trie[u].fail);
}
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
scanf("%s",modu+1);
insrt(modu,i);
}
get_fail();
scanf("%s",txt+1);
query(txt);
topo();
for(int i=1;i<=n;i++) printf("%lld\n",res[mp[i]]);
return 0;
}
这就是所谓的拓扑排序优化的 \(\mathfrak{AC}\) 自动机
然后我接着滚去 \(\texttt{写}\) \(\texttt{题}\) 了(悲
本文来自博客园,作者:冬天的雨WR,转载请注明原文链接:https://www.cnblogs.com/WintersRain/p/16732074.html
为了一切不改变的理想,为了改变不理想的一切

 浙公网安备 33010602011771号
浙公网安备 33010602011771号