[学习笔记]仙人掌&圆方树

1. 仙人掌

那么仙人掌是个什么玩意呢？

定义：对一个无向连通图，任意一条边属于至多一个简单环

仙人掌中共有两类边：

• 桥边：非环边，就是连接环的那些边
• 环边：就是环中的边嘛

 

 

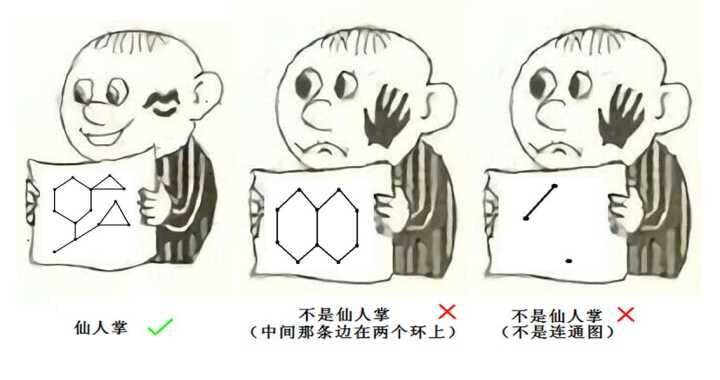
于是乎，我们获得了一张仙人掌图。

 

对于一个仙人掌，任意构建出一棵生成树。

然后我们就多了一些边——可以叫返祖边或者随便什么名字。

因为每条边只会出现在一个环中，所以每条返祖边都会覆盖树中的一条链，这条链+这条边构成了环。

所以我们可以确定每条边都出现在了哪个环中。

比如仙人掌的最大独立集，DP的时候只要额外的记录一下所在环的返祖边的端点的状态就ok。

考虑 这道例题

需要求一个仙人掌上最短距离

可以发现仙人掌问题的解决方法也不过就是参照树的解法，然后特判环上的情况，把环上的信息记录到一个点上

那么我们为什么不直接把仙人掌图变成一棵树呢？这样不是更方便嘛？

这就是圆方树

2. 圆方树

什么是圆方树？

顾名思义，这是一颗有圆点又有方点的树。

圆点就是原仙人掌中所有的点，方点是我们新添加进去的点。

比如这张图

 

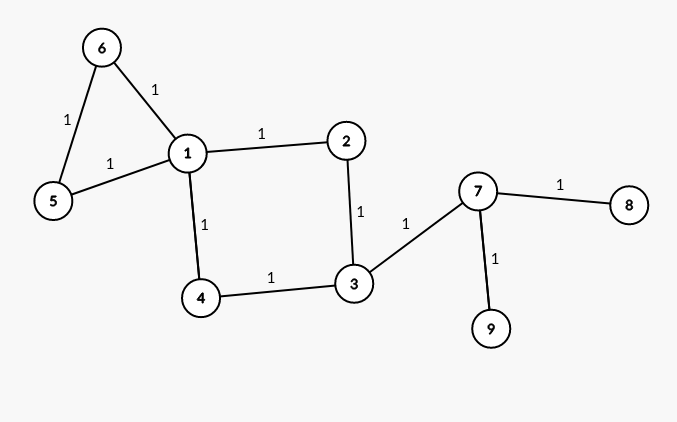
 （其实就是重新做了一下样例=_=）

别忘了，我们还要确定树的边权。

从一个点开始dfs，对于 $u\to v$ 的边：

• 如果是圆-圆边，我们选择直接保留边权
• 如果是方-圆边，我们再次分类：

1. 如果是方点和它的父亲的连边，我们把权值设置为 $0$
2. 如果是方点和其子结点的连边，我们把权值设置为这个子结点到方点父亲的最短距离长度（简单环上两点最短距离可 $\Theta(1)$ 求）

在上个图中，不妨以 $7$ 为根节点

那么圆方树就是这个样子的

 

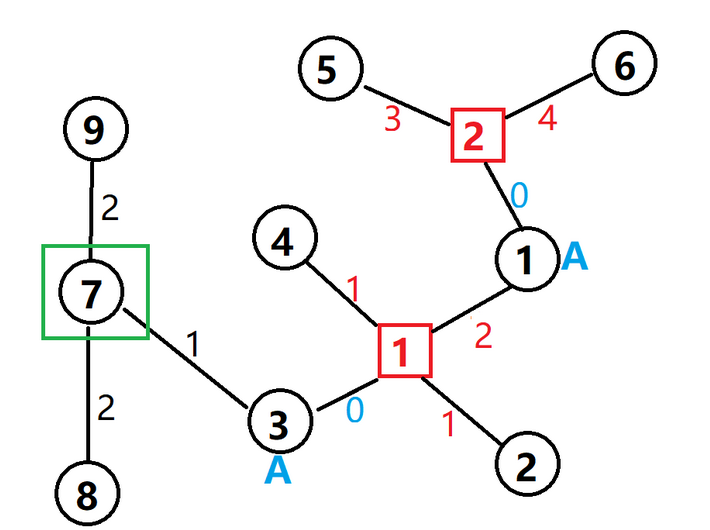
显然地，它具有一棵树的性质，在处理仙人掌时比较简便

为什么它是一棵树呢？

 

然后我们考虑如何求树上点的距离

直接 $\operatorname{LCA}$ 肯定是不行的，例如同一个环内的两点，他们的 $\operatorname{LCA}$ 是方点，而他们的距离却不是到方点的距离和。

我们需要分类讨论：

根据上面的边权定义可以知道，一个圆点和他的祖先圆点之间的距离一定是原图上两圆点之间的距离。

简单证明：（我们把一个环里的方点叫父亲结点，它的父亲就是爷爷结点了）

$\qquad$ 如果这两个点在一个环内，那么那个祖先一定是这个环上的爷爷，否则不可能成为祖先关系。

$\qquad$ 那么这两点间在新图上距离就是子孙圆点-方点-爷爷圆点，权值则是子孙结点到爷爷结点的最短距离，这与我们的定义相吻合。

$\qquad$ 如果这两个点不在同一个环内，那么他们的距离为子孙结点-子孙结点环内的爷爷结点-环与环之间的连边-第二个环上的与第一个环的爷爷相连的点-第二个环的爷爷 $\cdots\cdots$

这样一直下去，我们的最开始选的那个祖先结点一定是某个环的爷爷，或是与某个爷爷相连的点，无论哪种情况，权值都是对的（爷-孙权值是对的，环环之间的连边一定是圆-圆边，权值也是原来的）

其他情况大多数会与仙人掌的性质不符而错误，最终只剩下这两种情况。

所以如果两个点的 $\operatorname{LCA}$ 是圆点，那么他们的距离就是各自到 $\operatorname{LCA}$ 的距离，与平常的树上距离是一个求法。

如果两个点的 $\operatorname{LCA}$ 是方点，那么他们的距离是什么呢？

如果两个点的 $\operatorname{LCA}$ 是方点，那么某一个点的祖先中的 $\operatorname{LCA}$ 之前的那个祖先（也就是某个点到 $\operatorname{LCA}$ 这条链上的 $\operatorname{LCA}$ 的儿子结点）一定是与 $\operatorname{LCA}$ 这个方点在同一个环里面的。

假设 $a,b$ 是两个待求点，$fa_a,fa_b$ 是他们在 $\operatorname{LCA}$ 的环上距离他们最近的两个点（就是上面说的那个祖先），最短距离就是 $a$ 到 $fa_a$ 的距离 $+$ $b$ 到 $fa_b$ 的距离 $+$ $fa_a$ 到 $fa_b$ 的最短距离

由于 $a,b,fa_a,fa_b$ 都是圆点，$a$ 到 $fa_a$ ，$b$ 到 $fa_b$ 距离可以直接求，剩下 $fa_a$ 到 $fa_b$ 的距离就是简单环上两点间最短距离，可以 $\Theta(1)$ 求。

那么针对我们的例题，解法就很简单了

美中不足的是，代码好像有点长？

 

#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000,INF=1099588621776;
struct Edge{
    int pre,to,val;
};
struct TreeCut{
    Edge edge[WR<<1];
    int head[WR],tot;
    void add(int u,int v,int val){
        edge[++tot].pre=head[u];
        edge[tot].to=v;
        edge[tot].val=val;
        head[u]=tot;
    }
    int fa[WR],son[WR],sze[WR],dpt[WR],dis[WR];
    int top[WR];
    void dfs1(int u,int root){
        fa[u]=root,dpt[u]=dpt[root]+1,sze[u]=1;
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v==root) continue;
            dis[v]=dis[u]+edge[i].val;
            dfs1(v,u);
            sze[u]+=sze[v];
            if(sze[v]>sze[son[u]]) son[u]=v;
        }
    }
    void dfs2(int u,int tp){
        top[u]=tp;
        if(son[u]) dfs2(son[u],tp);
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
        }
    }
    int LCA(int x,int y){
        while(top[x]!=top[y]){
            if(dpt[top[x]]<dpt[top[y]]) swap(x,y);
            x=fa[top[x]];
        }
        if(dpt[x]<dpt[y]) return x;
        else return y;
    }
    int getfa(int u,int root){
        int res;
        while(top[u]!=top[root]){
            res=top[u];
            u=fa[top[u]];
        }
        if(u==root) return res;
        else return son[root];
    }
}tree;
int n,m,q;
int read(){
    int s=0,w=1;
    char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        s=(s<<3)+(s<<1)+ch-'0';
        ch=getchar();
    }
    return s*w;
}
Edge edge[WR];
int head[WR],tot;
int low[WR],ipt[WR],cnt;
int ring,fa[WR];
int rec[WR],sum[WR];
void add(int u,int v,int val){
    edge[++tot].pre=head[u];
    edge[tot].to=v;
    edge[tot].val=val;
    head[u]=tot;
}
void calc(int u,int v,int val){
    //这里u是起点，也是这个环的爷爷结点
    ring++;
    int preval=val,i=v;
    //这个环上其他的边权已经被保存在各个点上了，只剩下这个目前的val，它是这个环上的最后一个边权。
    while(i!=fa[u]){
        sum[i]=preval;
        //通过跳fa遍历这个环上的某一个点，并记录前缀和
        preval+=rec[i];
        i=fa[i];
    }
    sum[n+ring]=sum[u];//加了一个方点，其权值是整个环的权值和
    //默认方点的是大于n的，之后好处理
    i=v;
    sum[u]=0;
    int res;
    while(i!=fa[u]){
        res=min(sum[i],sum[n+ring]-sum[i]);
        //由于起点是爷爷结点，所以sum[i]就是i到爷爷结点的边权和
        //找每个点到u，也就是这个环上爷爷结点的最短距离。
        tree.add(n+ring,i,res);
        tree.add(i,n+ring,res);
        i=fa[i];
    }
}
void tarjan(int u){
    ipt[u]=low[u]=++cnt;
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(!ipt[v]){
            fa[v]=u;
            rec[v]=edge[i].val;
            //这个操作是记录一下每个点可能的环上的上一个结点，这里默认v的父亲是u，v上保存一下u到v的边权。
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(v!=fa[u]){
            low[u]=min(low[u],ipt[v]);
        }
        if(low[v]>ipt[u]){
            tree.add(u,v,edge[i].val);
            tree.add(v,u,edge[i].val);
            //如果low[v]>dfn[u]而u与v还是相连的，那他们一定是圆-圆边，直接把原边权加入新图
        }
    }
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(fa[v]==u||ipt[u]>=ipt[v]) continue;
        //如果u是某个环的起点，那他一定连接这某个环的两个点（由于仙人掌的性质，u必须也只能连接两个点）。
        //这两个点一个点是从u点出发的，他的fa值是u，剩下一个是转了一圈回来的，他一定在u之后被遍历。
        //我们要在这里找那个转了一圈回来的点（他fa值不为u，一定是由某个u的子结点遍历到的）。
        calc(u,v,edge[i].val);
    }
}
int solve(int x,int y,int lca){
    if(lca<=n){
        return tree.dis[x]+tree.dis[y]-2*tree.dis[lca];
    }else{
        int fax=tree.getfa(x,lca),fay=tree.getfa(y,lca);
        int res=tree.dis[x]-tree.dis[fax]+tree.dis[y]-tree.dis[fay];
        if(sum[fax]<sum[fay]) swap(fax,fay);
        res+=min(sum[fax]-sum[fay],sum[lca]-sum[fax]+sum[fay]);
        return res;
    }
}
signed main(){
    n=read(),m=read(),q=read();
    for(int i=1;i<=m;i++){
        int u=read(),v=read(),val=read();
        add(u,v,val);
        add(v,u,val);
    }
    tarjan(1);
    tree.dfs1(1,0);
    tree.dfs2(1,1);
    while(q--){
        int x=read(),y=read();
        int lca=tree.LCA(x,y);
        printf("%lld\n",solve(x,y,lca));
    }
    return 0;
}

 

然后我们考虑如何求仙人掌的直径问题

其实只要分开讨论圆点和方点，方点断环就好了啦qwq

 

#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<iostream>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000,INF=1099588621776;
struct Edge{
    int pre,to;
}edge[WR<<1];
int head[WR],tot;
int n,m;
int tmp[WR],dp[WR];
int fa[WR],ipt[WR],low[WR],cnt;
int q[WR],ans;
int read(){
    int s=0,w=1;
    char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        s=(s<<3)+(s<<1)+ch-'0';
        ch=getchar();
    }
    return s*w;
}
void add(int u,int v){
    edge[++tot].pre=head[u];
    edge[tot].to=v;
    head[u]=tot;
}
void calc(int x,int y){
    // cerr<<"calculating "<<x<<" "<<y<<endl;
    int sum=0;
    int i=y;
    while(i!=fa[x]){
        // cerr<<i<<endl;
        tmp[++sum]=dp[i];
        i=fa[i];
    }
    for(int i=1;i<=sum;i++) tmp[i+sum]=tmp[i];
    reverse(tmp+1,tmp+1+(sum<<1));
    int l=1,r=0;
    q[++r]=1;
    for(int i=2;i<=(sum<<1);i++){
        while(l<=r&&i-q[l]>(sum>>1)) l++;
        ans=max(ans,tmp[i]+tmp[q[l]]+i-q[l]);
        while(l<=r&&tmp[q[r]]-r<tmp[i]-i) r--;
        q[++r]=i;
    }
    for(int i=2;i<=sum;i++) dp[x]=max(dp[x],tmp[i]+min(i-1,sum-i+1));
}
void tarjan(int u){
    // cerr<<u<<endl;
    ipt[u]=low[u]=++cnt;
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(!ipt[v]){
            fa[v]=u;
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(v!=fa[u]){
            low[u]=min(low[u],ipt[v]);
        }
        if(low[v]>ipt[u]){
            ans=max(ans,dp[u]+dp[v]+1);
            dp[u]=max(dp[u],dp[v]+1);
        }
    }
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(fa[v]==u) continue;
        if(ipt[v]>ipt[u]) calc(u,v);
    }
}
signed main(){
    n=read(),m=read();
    for(int i=1;i<=m;i++){
        int k=read(),pre=read();
        for(int j=1;j<k;j++){
            int now=read();
            add(pre,now);
            add(now,pre);
            pre=now;
        }
    }
    tarjan(1);
    printf("%lld\n",ans);
    return 0;
}