[模板]虚树

虚树，顾名思义就是不存在的树。

1. 虚树是什么？

虚树常常被使用在树形 $\operatorname{DP}$ 中。

当一次询问仅涉及到整棵树中少量节点时，对整棵树进行 $\operatorname{DP}$ 在时间上无法接受

此时我们可以建立一棵仅包含部分关键节点的树（也就是虚树），将非关键边构成的链简化，在虚树上进行 $\operatorname{DP}$

虚树包含的节点为所有的询问点以及它们两两的LCA

比如下面的图片，如果我要询问的点是红色的点

那么虚树中包含的点就是红色的点（询问点）和蓝色的点（ $\operatorname{LCA}$ ）

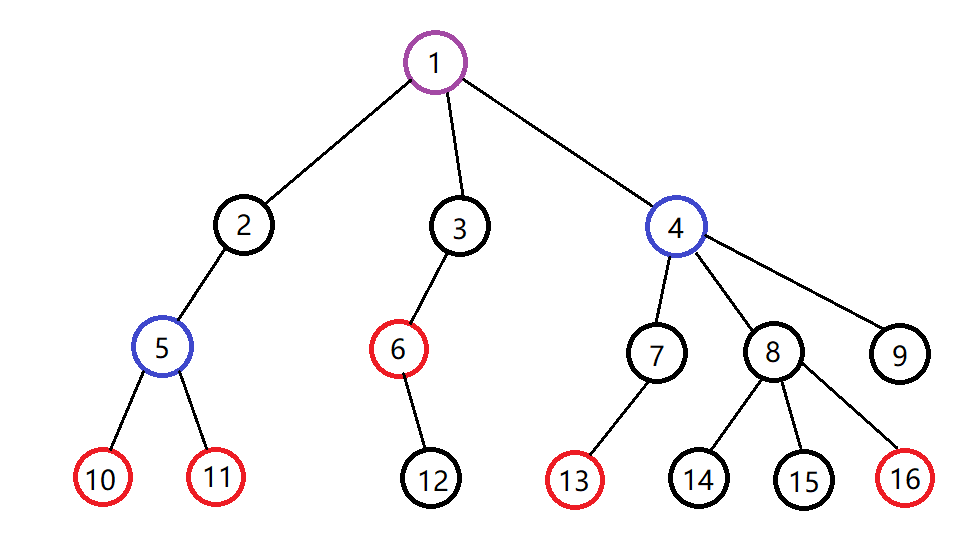
可以发现一号节点是紫色的，这是因为它既是询问点又是 $\operatorname{LCA}$

建立出来的虚树是这样的

 

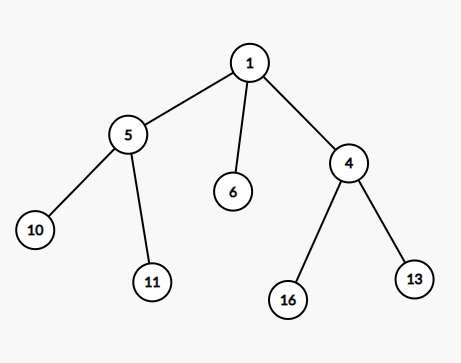
 显然虚树的叶子节点必定是询问点，因此对于一个大小为 $k$ 的询问，叶子节点至多有 $k$ 个，整棵树最多有 $2k-1$ 个节点

在实际操作中，我们一般选定一个点作为树的根（我一般是选 $1$ 号点）

这样可以避免很多麻烦

2. 准备工作

• 预处理出原树的 $\operatorname{DFS}$ 序
• 将询问点按照 $\operatorname{DFS}$ 序排序
• 高效的在线 $\operatorname{LCA}$ 算法（比如倍增，比如树链剖分）

说句闲话：其实倍增法没有树链剖分快

倍增法建立的复杂度是 $\Theta(n\log n)$ ，查询是 $\Theta(\log n)$

而树链剖分的复杂度是 $\Theta(n)$ ，查询也是 $\Theta(\log n)$

看上去貌似树剖更快，但 @Jijidawang 大佬指出在某些情况下ST表更优

我个人喜欢树剖，但有时候树剖写起来麻烦

 

struct Edge{
    int pre,to,val;
};
struct Tree_Cut{
    Edge edge[WR];
    int head[WR],tot=0;
    int sze[WR],fa[WR],son[WR],dpt[WR];
    int top[WR],rnk[WR],ipt[WR],cnt=0;
    void add(int u,int v,int val){
        edge[++tot].pre=head[u];
        edge[tot].to=v;
        edge[tot].val=val;
        head[u]=tot;
    }
    void dfs1(int u,int root){
        fa[u]=root,dpt[u]=dpt[root]+1,sze[u]=1;
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v==root) continue;
            dfs1(v,u);
            sze[u]+=sze[v];
            if(sze[v]>sze[son[u]]) son[u]=v;
        }
    }
    void dfs2(int u,int tp){
        top[u]=tp,ipt[u]=++cnt,rnk[cnt]=u;
        if(son[u]) dfs2(son[u],tp);
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v!=son[u]&&v!=fa[u]) dfs2(v,v);
        }
    }
    int LCA(int x,int y){
        while(top[x]!=top[y]){
            if(dpt[top[x]]<dpt[top[y]]) swap(x,y);
            x=fa[top[x]];
        }
        if(dpt[x]>dpt[y]) return y;
        else return x;
    }
}tree;

 

void dfs(int u,int root){
    dpt[u]=dpt[root]+1;
    for(int i=1;i<=17;i++){
        fa[u][i]=fa[fa[u][i-1]][i-1];
    }
    ipt[u]=++cnt,rnk[cnt]=u;
    for(int i=head[u];i;i=edge[i].pre){
        int v=edge[i].to;
        if(v==root) continue;
        fa[v][0]=u;
        dfs(v,u);
    }
}
int LCA(int x,int y){
    if(dpt[x]<dpt[y]) swap(x,y);
    for(int i=17;i>=0;i--){
        if(dpt[fa[x][i]]>=dpt[y]){
            x=fa[x][i];
        }
    }
    if(x==y) return res;
    for(int i=17;i>=0;i--){
        if(fa[x][i]!=fa[y][i]){
            x=fa[x][i],y=fa[y][i];
        }
    }
    return fa[x][0];
}

 

3. 建树

非常有趣的工作

引入一个概念：最右链

最右链的意思是在目前这条链的左边（不包括这条链）的虚树已经建设完毕

注意到最右链并没有被并入虚树里，这是因为还会不断地有求出的 $LCA$ 插进最右链中

在建树的最后一步我们将会清空栈，将最右链并入虚树

初始无条件将树根并入栈中（这里建议数组模拟栈，否则可能会比较麻烦）

然后将所有询问点顺次加入，同时加入当前询问点 $now$ 和栈顶元素 $stk[top]$ 的最近公共祖先 $lca$

这里要大力分类讨论：

Case 1：lca=stk[top]

这种情况的意思是 $now$ 在 $stk[top]$ 的子树中

 

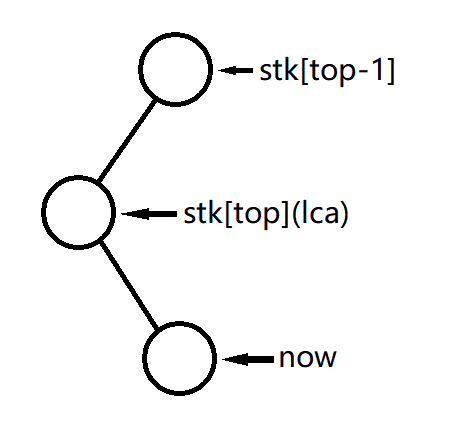
 对于这种情况，直接把 $now$ 加到栈顶就好

Case 2：lca在stk[top]和stk[top-1]之间

 

 

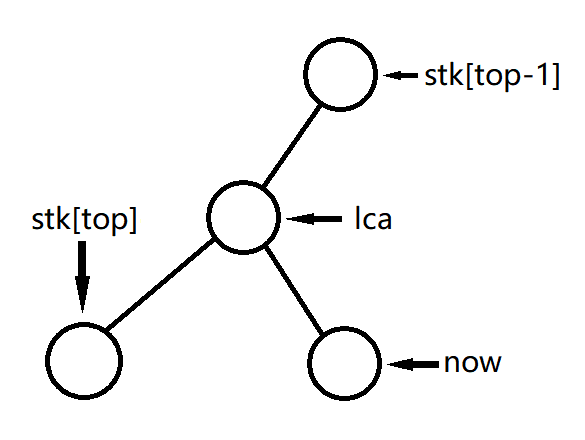
 此时最右链末端从 $stk[top-1] \to stk[top]$ 变为 $stk[top-1] \to lca \to now$

 也就是说我们先让 $stk[top]$ 出栈，再让 $lca$ 和 $now$ 入栈即可

 注意弹栈后要将 $lc$ 和 $stk[top]$ 连边

Case 3：lca=stk[top−1]

 

 

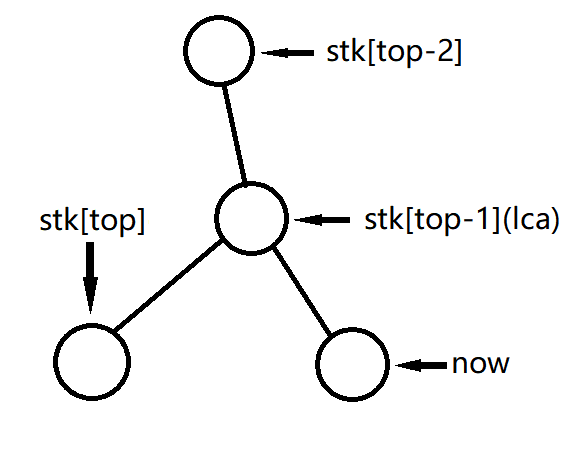
 和 $Case 2$ 基本相同，只不过不用再让 $lca$ 入栈，直接入栈 $now$ 即可

Case 4：dpt[lca]<dpt[stk[top]-1]

此时 $lca$ 已经不在 $stk[top-1]$ 的子树里了，甚至也可能不在 $$stk[top-2],stk[top-3]\cdots$ 的子树中

 

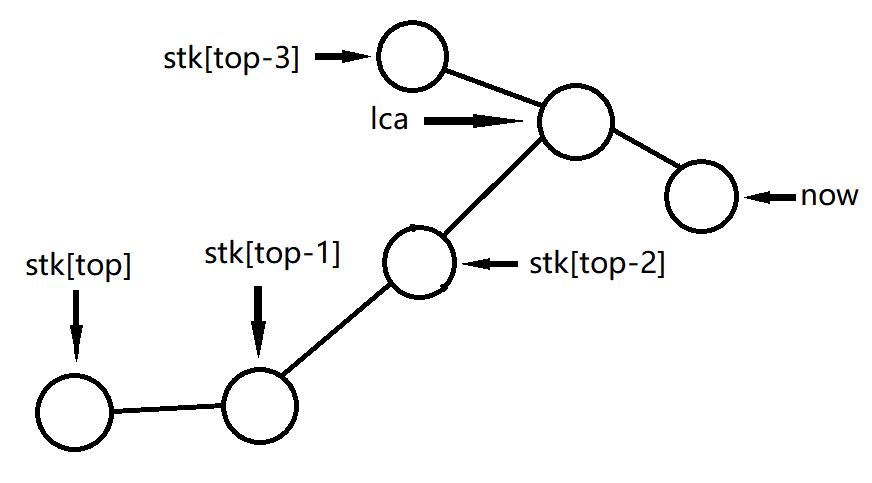
 如图，我们进行两次操作

第一次操作：循环将最右链顶端弹出，剪下的边加入虚树，直到不再是 $Case 4$

第二次操作：根据实际情况将 $now$ 入栈

 

在建树的最后，我们清空栈，将栈中元素连边

 

bool cmp(int x,int y){
    return tree.ipt[x]<tree.ipt[y];
}
void build(){
    sort(a+1,a+1+k,cmp);//按照DFS序大小排序
    top=1;stk[top]=1;
    tot=0;//清空
    for(int i=1;i<=k;i++){
        if(a[i]==1) continue;
        int lca=tree.LCA(a[i],stk[top]);
        if(lca!=stk[top]){//-------------------------------如果是Case 1直接跳过
            while(tree.dpt[lca]<tree.dpt[stk[top-1]]){//---Case 4
                int u=stk[top],v=stk[top-1];
                add(u,v);add(v,u);
                top--;
            }
            if(tree.dpt[lca]>tree.dpt[stk[top-1]]){//------Case 2
                int u=lca,v=stk[top];
                add(u,v);add(v,u);
                stk[top]=lca;
            }else{//---------------------------------------Case 3
                int u=lca,v=stk[top];
                add(u,v);add(v,u);
                top--;
            }
        }
        stk[++top]=a[i];
    }
    for(int i=1;i<top;i++){//最后统一清空栈进行连边
        int u=stk[i],v=stk[i+1];
        add(u,v);add(v,u);
    }
}    
建树

 

4. 清空

这里要注意的是我们不能在最后统一清空 $head$ 等数组，$\Theta(n)$ 的时间复杂度无法承受

所以我们在树形 $\operatorname{DP}$ 的末尾进行清空

然后我们会发现模板中只需要清空 $head$ 和 $vis$ 两个数组就好了

 

整个模板放一下

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#define int long long
#define WR WinterRain
using namespace std;
const int WR=1001000,INF=2147483647;
struct Edge{
    int pre,to;
};
struct Tree_Cut{
    Edge edge[WR];
    int head[WR],tot=0;
    int sze[WR],fa[WR],son[WR],dpt[WR];
    int top[WR],rnk[WR],ipt[WR],cnt=0;
    void add(int u,int v){
        edge[++tot].pre=head[u];
        edge[tot].to=v;
        head[u]=tot;
    }
    void dfs1(int u,int root){
        fa[u]=root,dpt[u]=dpt[root]+1,sze[u]=1;
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v==root) continue;
            dfs1(v,u);
            sze[u]+=sze[v];
            if(sze[v]>sze[son[u]]) son[u]=v;
        }
    }
    void dfs2(int u,int tp){
        top[u]=tp,ipt[u]=++cnt,rnk[cnt]=u;
        if(son[u]) dfs2(son[u],tp);
        for(int i=head[u];i;i=edge[i].pre){
            int v=edge[i].to;
            if(v!=son[u]&&v!=fa[u]) dfs2(v,v);
        }
    }
    int LCA(int x,int y){
        while(top[x]!=top[y]){
            if(dpt[top[x]]<dpt[top[y]]) swap(x,y);
            x=fa[top[x]];
        }
        if(dpt[x]>dpt[y]) return y;
        else return x;
    }
}tree;
Edge edge[WR];
int n,m,k;
int a[WR],stk[WR],top;
int head[WR],tot;
bool vis[WR];
int read(){
    int sze=0,w=1;
    char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        sze=(sze<<3)+(sze<<1)+ch-48;
        ch=getchar();
    }
    return sze*w;
}
bool cmp(int x,int y){
    return tree.ipt[x]<tree.ipt[y];
}
void add(int u,int v){
    edge[++tot].pre=head[u];
    edge[tot].to=v;
    head[u]=tot;
}
void build(){
    sort(a+1,a+1+k,cmp);
    top=1;stk[top]=1;
    tot=0;
    for(int i=1;i<=k;i++){
        if(a[i]==1) continue;
        int lca=tree.LCA(a[i],stk[top]);
        if(lca!=stk[top]){
            while(tree.dpt[lca]<tree.dpt[stk[top-1]]){
                int u=stk[top],v=stk[top-1];
                add(u,v);add(v,u);
                top--;
            }
            if(tree.dpt[lca]>tree.dpt[stk[top-1]]){
                int u=lca,v=stk[top];
                add(u,v);add(v,u);
                stk[top]=lca;
            }else{
                int u=lca,v=stk[top];
                add(u,v);add(v,u);
                top--;
            }
        }
        stk[++top]=a[i];
    }
    for(int i=1;i<top;i++){
        int u=stk[i],v=stk[i+1];
        add(u,v);add(v,u);
    }
}    
int dp(int u,int root){
    int res=0;
    //这里写普通的树形DP
    vis[u]=0,head[u]=0;
    return res;
}
signed main(){
    n=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        tree.add(u,v);
        tree.add(v,u);
    }
    tree.dfs1(1,0);
    tree.dfs2(1,1);
    m=read();
    while(m--){
        k=read();
        for(int i=1;i<=k;i++) a[i]=read(),vis[a[i]]=true;
        build();
        printf("%lld\n",dp(1,0));
    }
    return 0;
}